Exercices : Théorème de Thalès – 3ac

Soit $ABC$ un triangle, tels que :
$AB=5cm$, $AC=8cm$, $BC=6cm$

$I$ un point de $[AB]$ tel que $IA=2cm$, et
$J$ un point de $[AC]$, tel que $(IJ)\parallel (BC)$

1. Faire une figure.
2. Calculer les distances $JA$, $JC$ et $IJ$

Soit $ABC$ un triangle tels que :
$AB=5cm$; $AC=10cm$ et $BC=8cm$.

$E$ un point de $[AB]$ tel que $AE=2cm$ et $F$ un point de $[AC]$ tel que $AF=4cm $

1. Faire une figure.
2. Montrer que : $(EF)\parallel(BC)$.
3. La droite passant par le point $B$ parallèlement à $(EC)$ coupe $(AC)$ en $K$. Calculer $CK$

$ABCD$ est un parallélogramme.
Soient $E$ et $I$ deux points de $[AB]$ et $[AC]$ respectivement tels que:
$(IE)\parallel (BC)$ et $AB=10$; $BC=8$; $AI=3$ et $AE=6$.

1. Calculer $AC$ et $IE$.
2. Soit $F$ un point de $[AD]$ tel que : $AF=4,8$.
   1. Comparer les rapports : $\dfrac{AI}{AC}$ et $\dfrac{AF}{AD}$.
   2. En déduire que les droites $(IF)$ et $(DC)$ sont parallèles.
3. Montrer que les droites $(BD)$ et $(EF)$ sont parallèles.

Dans la figure suivante les droites $(AC)$ et $(EF)$ sont parallèles.
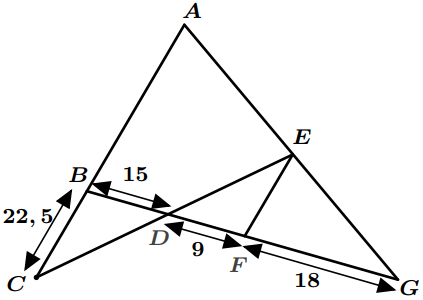Calculer $AB$.

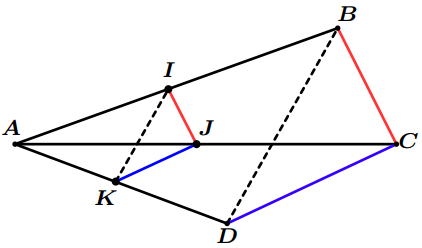
Dans la figure suivante :

• Les droite $(IJ)$ et $(BC)$ sont parallèles.
• Les droite $(JK)$ et $(CD)$ sont parallèles.

Montrer que les droites $(IK)$ et $(BD)$ sont parallèles.

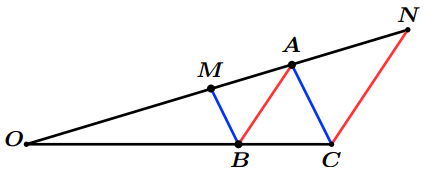
Dans la figure suivante :

• Les droite $(MB)$ et $(AC)$ sont parallèles.
• Les droite $(AB)$ et $(NC)$ sont parallèles.

En utilisant le théorème de Thalès, Démontrer que : $OA^2=OM\times ON$.