Examen National de Mathématiques - Sciences maths - Session de Rattrapage 2025

ⓘ

Examen National du Baccalauréat
Epreuve de Mathématiques
Session de rattrapage 2025

Filières : Sciences Mathématiques A et B
Durée : 4 heures

Exercice 1 Mathxi math

- type [Signaler une erreur]

Enoncé

Partie I :
On considère la fonction $f$ définie sur l’intervalle $I = [0; +\infty[$ par :
$$
f(0) = 0 \quad \text{et} \quad f(x) = \frac{x^2 \ln x}{x^2 + 1} \quad \text{si} \quad x \in ]0; +\infty[
$$
Et soit $(C)$ la courbe représentative de la fonction $f$ dans un repère orthonormé $(O, \vec{i}, \vec{j})$.

1. Étudier la continuité de $f$ à droite en 0
2. Étudier la dérivabilité de $f$ à droite en 0 puis interpréter graphiquement le résultat obtenu.
3. Calculer $\displaystyle\lim_{x \to +\infty} f(x) $ et $\displaystyle\lim_{x \to +\infty} \dfrac{f(x)}{x}$ puis interpréter graphiquement le résultat obtenu.
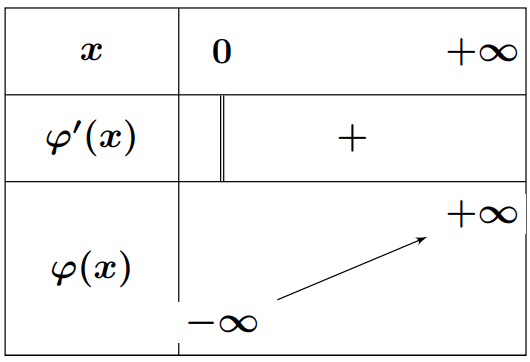
Soit $\varphi$ la fonction définie sur $]0; +\infty[$ par : $ \varphi(x) = x^2 + 1 + 2 \ln x $
1. Dresser le tableau de variations de $\varphi$
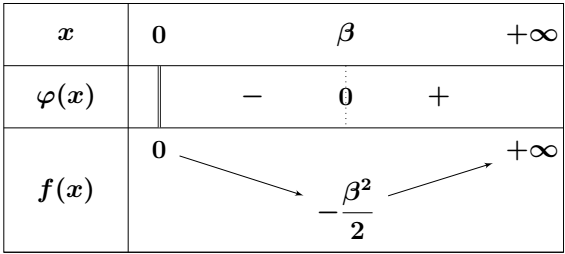
2. Montrer que l’équation $ \varphi(x) = 0 $ admet une solution unique $\beta$ appartenant à l’intervalle
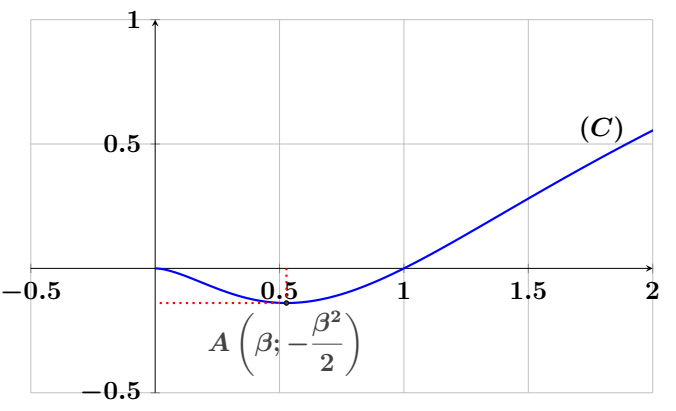
  $ \left[ \dfrac{1}{2} ; \dfrac{1}{\sqrt{3}} \right] $ (On donne $ \ln 2 \simeq 0{,}7 $ et $ \ln 3 \simeq 1{,}1 $)
3. Montrer que : $ f(\beta) = -\dfrac{\beta^2}{2} $
1. Montrer que $f$ est dérivable sur $]0; +\infty[$ et que $\left(\forall x \in ]0; +\infty[\right),\quad f'(x) = \dfrac{x \varphi(x)}{(x^2 + 1)^2}$
2. Donner le tableau de variations de $f$
3. Montrer que $ \dfrac{1}{\beta} $ est l’unique solution de l’équation $ f(x) = \dfrac{1}{2} $ sur $ ]\beta; +\infty[ $
4. Montrer que la droite d’équation $ y = \beta x -\dfrac{1}{2} $ est la tangente à la courbe $(C)$ au point d’abscisse $ \dfrac{1}{\beta} $
Représenter graphiquement la courbe $(C)$ dans le repère $(O, \vec{i}, \vec{j})$
(On admet que la courbe $(C)$ possède deux points d’inflexion)

Partie II :
On pose : $ J = \left] \sqrt{3}; 2 \right] \quad \text{et} \quad \alpha = \dfrac{1}{\beta}$
Soit $g$ la fonction définie sur $]0; +\infty[$ par : $ g(x) = \sqrt{e^{1+\frac{1}{x^2}}} $

1. Étudier les variations de $g$
2. Montrer que : $\left(\forall x \in J\right), \quad \sqrt{3} < g(x) < 2$
  (On donne $ \sqrt{3} \simeq 1{,}73$, $ e^{1/2} \simeq 1{,}95$ et $ e^{5/6} \simeq 1{,}87$)
1. En utilisant le résultat de la question I.3-c), montrer que : $ g(\alpha) = \alpha $
2. Montrer que : $\left( {\forall x \in J} \right);\quad \left| {g’\left( x \right)} \right| \le \dfrac{2}{{3\sqrt 3 }}$
3. En déduire que : $\left( {\forall x \in J} \right);\quad \left| {g\left( x \right) -\alpha } \right| \le \dfrac{2}{{3\sqrt 3 }}\left| {x -\alpha } \right|$
On considère la suite $(x_n)_{n\in\mathbb{N}}$ définie par : $$x_0=\dfrac{7}{4}\quad\text{et pour tout } n\in\mathbb{N},\quad x_{n+1}=g(x_n)$$
1. Montrer que : $\left( {\forall x \in \mathbb{N}} \right);\quad {x_n} \in J$
2. Montrer par récurrence que : $\left( {\forall x \in \mathbb{N}} \right);\quad \left| {{x_n} -\alpha } \right| \le {\left( {\dfrac{2}{{3\sqrt 3 }}} \right)^n}\left| {{x_0} -\alpha } \right|$
3. En déduire que la suite $(x_n)_{n\in\mathbb{N}}$ converge vers $\alpha$.

Indication math

Partie I :
1. Pour montrer que $f$ est continue à droite en $0$, calculez la limite :
  $$
  \lim_{x \to 0^+} f(x)
  $$
  et comparez-la à $f(0)$.
2. Utilisez la définition de la dérivabilité à droite en $0$ :
  $$
  \lim_{x \to 0^+} \frac{f(x) -f(0)}{x}
  $$
  Si cette limite existe, elle donne la pente de la tangente à la courbe $(C)$ à l’origine.
3. Calculez séparément :
  $$
  \lim_{x \to 0^+} f(x) \quad \text{et} \quad \lim_{x \to 0^+} \frac{f(x)}{x}
  $$
  Pour la deuxième limite, pensez à simplifier $f(x)$ comme un produit de $x$ et $\frac{\ln x}{x^2 + 1}$.
Soit $\varphi(x) = x^2 + 1 + 2 \ln x$
1. Dérivez $\varphi$ :
  $$
  \varphi'(x) = 2x + \frac{2}{x}
  $$
  puis étudiez le signe de cette dérivée pour déterminer les variations de $\varphi$.
2. Utilisez la continuité et la stricte monotonie de $\varphi$ sur l’intervalle donné pour appliquer le théorème des valeurs intermédiaires.
3. Utilisez que $\varphi(\beta) = 0$ pour simplifier $f(\beta)$ :
  $$
  f(\beta) = \frac{-\beta^2 \ln \beta}{\beta^2 + 1}
  $$
  puis remplacez $\ln \beta$ par $-\frac{\beta^2 + 1}{2}$.
1. Appliquez la formule de la dérivée d’un quotient :
  $$
  f(x) = \frac{-x^2 \ln x}{x^2 + 1}
  $$
  Utilisez :
  $$
  f'(x) = \frac{(u’v -uv’)}{v^2}
  $$
  avec $u = -x^2 \ln x$ et $v = x^2 + 1$.
2. Utilisez le signe de $\varphi(x)$ pour déterminer le signe de $f'(x)$ et dresser le tableau de variations de $f$.
3. Étudiez l’équation :
  $$
  f(x) = \frac{1}{2}
  $$
  sur $]\beta; +\infty[$, et utilisez la stricte monotonie de $f$ pour montrer l’unicité de la solution.
4. Vérifiez que :
  $$
  f\left( \frac{1}{\beta} \right) = \frac{1}{2}
  $$
  et que :
  $$
  f’\left( \frac{1}{\beta} \right) = \beta
  $$
  puis utilisez la formule de la tangente :
  $$
  y = f(a) + f'(a)(x -a)
  $$
  pour montrer que la droite a pour équation :
  $$
  y = \beta x -\frac{1}{2}
  $$
Appuyez-vous sur :
- le tableau de variations de $f$
- les limites en $0$ et à l’infini
- les tangentes connues
Tracez la courbe $(C)$ en indiquant les points notables et la concavité (points d’inflexion).

Partie II :

1. Posez $g(x) = \sqrt{e^{\frac{1 + x}{x}}}$ et utilisez la dérivée d’une composition pour obtenir $g'(x)$. Puis étudiez son signe sur $]0; +\infty[$.
2. Calculez quelques valeurs approchées de $g(x)$ aux bornes de $J$. Utilisez les encadrements donnés pour établir l’inégalité :
  $$
  \sqrt{3} < g(x) < 2 $$
1. Rappelez que :
  $$
  \alpha = \frac{1}{\beta}
  $$
  puis remplacez dans $g$ :
  $$
  g(\alpha) = \sqrt{e^{\frac{1 + \alpha}{\alpha}}}
  $$
  Utilisez le fait que $f(\alpha) = \frac{1}{2}$ pour retrouver $\beta$.

Corrigé