Évaluation diagnostique maths TC.SC

Déterminez une opération pour ce qui suit : $A=\left( {2x- 1} \right)\left( {x- 4} \right) + \left( {2x- 1} \right)\left( {-3x + 5} \right)$

1. $A=\left( {2x- 1} \right)\left( {-2x+ 1} \right)$
2. $A=\left( {2x- 1} \right)\left( {4x+ 1} \right)$
3. $A=\left( {2x- 1} \right)\left( {x- 4} \right)\left( {-3x+ 5} \right)$
4. $ A=- 2\left( {2x- 1} \right)$

Observez la figure suivante :

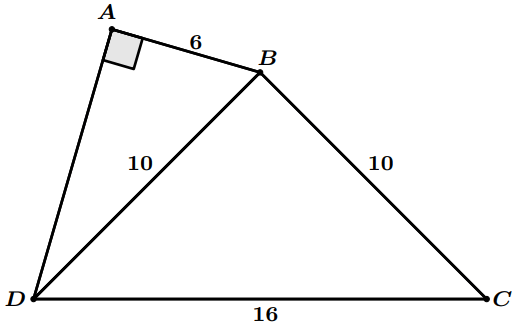
Q1. Le triangle $BCD$ est-il rectangle? Oui ou non.

Q2. Calculer $\mathcal{p}$ le périmètre de la figure $ABCD$

1. $\mathcal{p}=40$
2. $\mathcal{p}=50$
3. $\mathcal{p}=60$
4. $\mathcal{p}=30$

Calculer  : $B=\dfrac{14}{5-\sqrt{11}}-\dfrac{11}{\sqrt{11}}$

1. $B=5\sqrt{11}$
2. $B=5+\sqrt{11}$
3. $B=5$
4. $B=\dfrac{5}{11-5\sqrt{11}}$

Dans la figure suivante, $ABCD$ est un rectangle tel que $AB=4 cm$ et $AD=3 cm$. Soit $M$ un point du segment $[AB]$ et $N$ un point du segment $[BC]$ tels que $AM=x$ et $CN=1cm$.

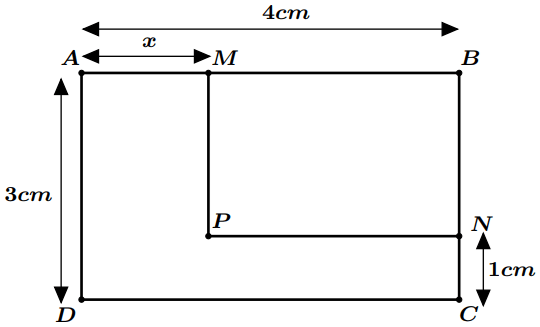
Sachant que l’aire du rectangle $ABCD$ est trois fois celle du rectangle $BNPM$.
Déterminer la valeur de $x$.

1. $4cm$
2. $2cm$
3. $1cm$
4. $3cm$

Dans la figure suivante, les triangles $ABC$ et $ACD$ sont rectangles avec : $\widehat {BAC} = \widehat {CAD} = \alpha $.

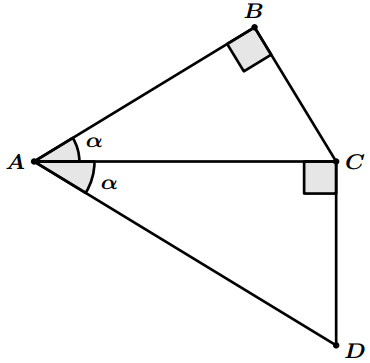
Déterminer la valeur de $cos^2 \alpha$ parmi les expressions suivantes :

1. $\dfrac{AB}{BC}$
2. $\dfrac{AD}{AB}$
3. $\dfrac{AB}{DC}$
4. $\dfrac{AB}{AD}$

Soit $a$ un nombre réel positif. Développez l’expression suivante : $C={\left( {\sqrt a + 2} \right)^2} + {\left( {2\sqrt a – 1} \right)^2}$

1. $C=5a+5$
2. $C=a+2\sqrt a +5$
3. $C=5a+3$
4. $C=a+2\sqrt a+3$
5. $C=3a+5$

Soit $ABCD$ un carré inscrit dans un cercle de centre $O$ et de rayon $6$. Soit $H$ le projeté orthogonal de $O$ sur $(AB)$ (voir la figure).

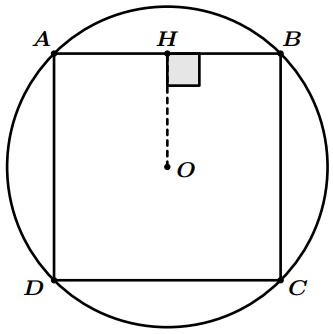
Calculer la distance $OH$.

1. $OH=\sqrt 6$
2. $OH=3\sqrt 2$
3. $OH=3$
4. $OH=2\sqrt 6$

Considérons dans un repère orthonormé ${\left( {O;\vec i;\vec j} \right)}$ les points $A(1;2)$, $B(-1;1)$, $C(-2;-2)$ et $D(x;y)$.
Déterminer les coordonnées du point $D$ sachant que le quadrilatère $ABCD$ est un parallélogramme.

1. $D(1;-1)$
2. $D(0;1)$
3. $D(0;-1)$
4. $D(-1;0)$

Considérons dans un repère orthonormé ${\left( {O;\vec i;\vec j} \right)}$ les points $A(2;1)$ et $B(-3;2)$.
Déterminer l’équation réduite de la droite $(AB)$.

1. $y = \dfrac{{- 1}}{5}x + \dfrac{7}{5}$
2. $y = \dfrac{1}{5}x- \dfrac{7}{5}$
3. $y = \dfrac{{- 1}}{5}x- \dfrac{7}{5}$
4. $y = \dfrac{1}{5}x+ \dfrac{7}{5}$

Quel est le nombre égal à : $$D=\dfrac{3}{5} \times {\left( {\dfrac{3}{5}} \right)^4} \times {\left( {\dfrac{{ – 3}}{5}} \right)^3}$$

1. $D={\left( {\dfrac{{- 3}}{5}} \right)^8}$
2. $D=- {\left( {\dfrac{3}{5}} \right)^{12}}$
3. $D=- {\left( {\dfrac{3}{5}} \right)^7}$
4. $D=- {\left( {\dfrac{3}{5}} \right)^8}$

$OMN$ est un triangle et $P$ un point du segment $[OM]$ et $R$ un point du segment $|ON]$ tels que le segment $[PR]$ est parallèle au segment $[MN]$.

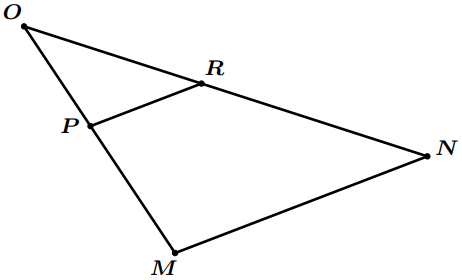
On donne : $OP=x$, $PM=3$, $OR=5$ et $RN=6$.
Déterminer la valeur de $x$.

1. $3$
2. $2,5$
3. $2$
4. $1,5$

Quel est le nombre égal à : $E=5,12 \times 10^3 $ ?

1. $E=512$
2. $E=5,12$
3. $E=5120$
4. $E=512000$

Sur le schéma suivant, placez le point $N$ tel que $\overrightarrow {MN\,} = \overrightarrow {AB\,} + \overrightarrow {AC\,} $.

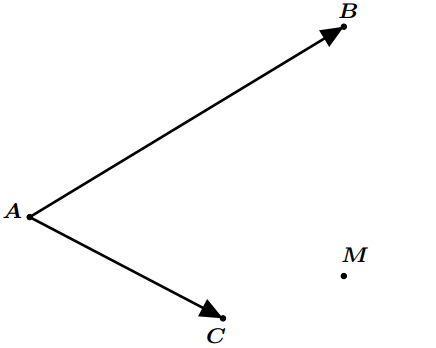
Le périmètre d’un rectangle est de $284 m$. Quelle est (en mètres) la longueur de ce rectangle sachant que sa longueur dépasse sa largeur de $12 m$?

1. $65m$
2. $142m$
3. $77m$
4. $12m$

Soit le nombre réel $x$ tel que : $ – 3 < 2x + 3 < 5$
Donner un encadrement du nombre $1-x$.

1. $ – 3 < 1 – x < 0$
2. $0 < 1 – x < 4$
3. $4 < 1 – x < 5$
4. $-2 < 1 – x < -1$

$ABC$ est un triangle isocèle en $A$ tel que $\widehat {BAC} = 80^\circ$. $M$ est un point de l’arc $\overset{\huge\frown}{AC}$ ne contenant pas $B$.

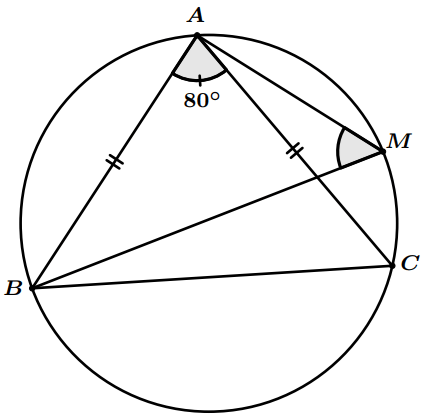
Quelle est la mesure de l’angle $\widehat {BMA}$?

1. $40°$
2. $130°$
3. $100°$
4. $50°$

Donnez tous les arêtes du parallélépipède parallèles à l’arête $[AB]$.

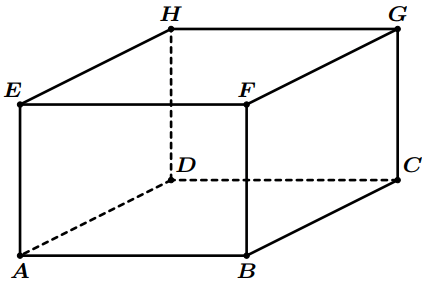
$ABCDEFGH$ est un cube dont l’arête mesure $5$.

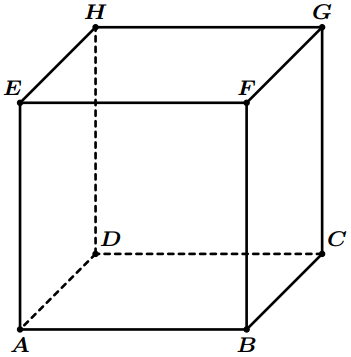
Quelle est la longueur de la diagonale $[BH]$?

1. $BH=5\sqrt 3$
2. $BH=5$
3. $BH=5\sqrt 2$
4. $BH=3\sqrt 5$

Le tableau ci-dessous représente la répartition des distances $d$ (en $km$) parcourues par les élèves de certains villages pour rejoindre leur collège.

Nombre d’enfants	$0 \le d < 1$	$1 \le d < 2$	$2 \le d < 3$	$3 \le d < 4$	$4 \le d < 5$
Nombre de familles	$50$	$60$	$70$	$80$	$40$

Quelle est le pourcentage d’élèves de ces villages qui parcourent une distance supérieure ou égale à $3 km$?

1. $60\%$
2. $80\%$
3. $40\%$
4. $70\%$