ⓘ
Devoir surveillé n°3
Premier Semestre
Niveau : 3èm année collège
Leçons ciblées : Pythagore, Trigonométrie, Angles inscrits, Triangles semblables.
Enoncé 
Soit $ABC$ un triangle tels que : $AB=3$, $AC=\sqrt{3}$ et $BC=2\sqrt{3}$
-
- Montrer que $ABC$ est un triangle rectangle en $A$.
- Calculer $\sin \widehat {ABC}$.
- Soit $M$ est le milieu de $[AB]$ et $H$ sa projection orthogonale sur $(BC)$.
- Montrer que : $MH=\dfrac{3}{4}$
- Calculer la distance $HB$.
Indication 
-
-
Calculer les carrés des côtés du triangle $ABC$ afin d’appliquer la réciproque du théorème de Pythagore.
-
Utiliser le fait que $ABC$ est un triangle rectangle en $A$ pour écrire :
$$\sin \widehat{ABC} = \dfrac{\text{côté opposé à } \widehat{B}}{\text{hypoténuse}}.$$
-
-
Exprimer le sinus de l’angle $\widehat{B}$ dans les deux triangles $ABC$ et $BHM$, puis comparer les deux expressions pour en déduire $MH$.
-
Exprimer le cosinus de l’angle $\widehat{B}$ dans les deux triangles $ABC$ et $BHM$,
ou bien utiliser directement le théorème de Pythagore dans le triangle $BHM$ pour calculer $HB$.
Corrigé 
-
- Montrer que $ABC$ est un triangle rectangle en $A$.Calculons les carrés des longueurs :$$\begin{aligned}
&AB^2 = 3^2 = 9,\\
&AC^2 = (\sqrt{3})^2 = 3,\\
&BC^2 = (2\sqrt{3})^2 = 4\times 3 = 12
\end{aligned}$$On remarque que : $9 + 3 = 12$, c’est-à-dire : $$AB^2 + AC^2 = 12 = BC^2.$$Par la réciproque du théorème de Pythagore, le triangle $ABC$ est rectangle en $A$.
- Calculer $\sin \widehat{ABC}$. Dans le triangle $ABC$ rectangle en $A$, l’angle $\widehat{ABC}$ est un angle aigu en $B$. Le côté opposé à $\widehat{ABC}$ est $AC$ et l’hypoténuse est $BC$. Donc :$$\sin\widehat{ABC}=\dfrac{AC}{BC}=\dfrac{\sqrt{3}}{2\sqrt{3}}=\dfrac{1}{2}.$$
Résultat : $\sin\widehat{ABC}=\dfrac{1}{2}$.
- Soit $M$ le milieu de $[AB]$ et $H$ sa projection orthogonale sur $(BC)$. (Voir la figure)
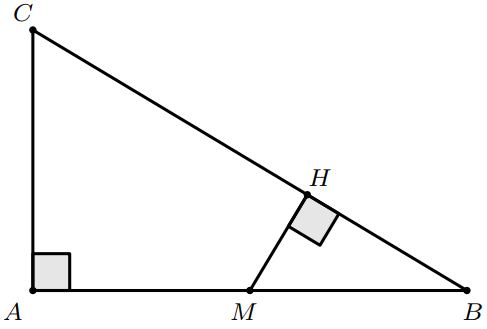
- Montrer que : $MH=\dfrac{3}{4}$.
D’une part, dans le triangle $BHM$ rectangle en $H$, on a :$$\sin \widehat{B} = \dfrac{MH}{BM}.$$
D’autre part, dans le triangle $ABC$ rectangle en $A$, on a :
$$\sin \widehat{B} =\dfrac{1}{2}.$$
On déduit que :
$$\dfrac{MH}{BM} = \dfrac{1}{2}$$
Alors : $$MH = \dfrac{BM}{2}.$$
Or, $M$ est le milieu de $[AB]$, donc :
$$BM = \dfrac{AB}{2} = \dfrac{3}{2}.$$
Donc :
$$MH = \dfrac{\tfrac{3}{2}}{2} = \dfrac{3}{4}.$$
Conclusion : $MH=\dfrac{3}{4}$.
- Calculer la distance $HB$.
D’une part, dans le triangle $BHM$ rectangle en $H$, on a :$$\cos \widehat{B} = \dfrac{HB}{BM}.$$
D’autre part, dans le triangle $ABC$ rectangle en $A$, on a :
$$\cos \widehat{B} =\dfrac{AB}{BC}=\dfrac{3}{2\sqrt 3}=\dfrac{\sqrt 3}{2}.$$
On déduit que :
$$\dfrac{HB}{BM} = \dfrac{\sqrt 3}{2}$$
Alors : $$HB = \dfrac{\sqrt 3 BM}{2}=\dfrac{\sqrt 3\times \frac{3}{2}}{2}=\dfrac{3\sqrt 3}{4}.$$
Conclusion : $HB=\dfrac{3\sqrt 3}{4}$.
Enoncé 
- Soit $EFG$ un triangle rectangle en $G$ tel que : $\cos {\widehat {GEF}} = \dfrac{{\sqrt 3 }}{3}$ et $EG=\sqrt{3}$
- Calculer $EF$ et $FG$.
- Calculer $\sin\widehat{EFG}$, $\cos\widehat{EFG}$ et $\tan\widehat{EFG}$
- Simplifier les expressions suivantes :
- $U = \sin 30^\circ -\sin 45^\circ -\cos 60^\circ + \tan 60^\circ $
- $V = \tan 15^\circ -\dfrac{1}{{\tan 75^\circ }} -\cos 10^\circ + \sin 80^\circ $
- Soit $\alpha$ la mesure d’un angle aigu.Sachant que $\sin\alpha=\dfrac{1}{7}$, calculer $\cos\alpha$ et $\tan\alpha$.
Indication 
-
- Utiliser la définition de $\cos \widehat{GEF}=\dfrac{EG}{EF}$ avec les données de l’énoncé pour trouver $EF$, puis appliquer le théorème de Pythagore pour déterminer $FG$.
- Rappeler les définitions :
$$\begin{aligned}
&\sin(\widehat{EFG})=\dfrac{\text{côté opposé}}{\text{hypoténuse}},\\
&\cos(\widehat{EFG})=\dfrac{\text{côté adjacent}}{\text{hypoténuse}}\\
&\tan(\widehat{EFG})=\dfrac{\text{opposé}}{\text{adjacent}}.
\end{aligned}$$
-
- Rappeler les valeurs exactes :
$$\begin{aligned}
&\sin 30^\circ=\dfrac12,\ \quad \sin 45^\circ=\dfrac{\sqrt{2}}{2},\\
&\cos 60^\circ=\dfrac12,\ \quad \tan 60^\circ=\sqrt{3}.
\end{aligned}$$
- Utilise les relations suivantes,
$$\begin{aligned}
&\sin(90^\circ-\theta)=\cos\theta, \quad \cos(90^\circ-\theta)=\sin\theta\\
&\tan(90^\circ-\theta)=\dfrac{1}{\tan\theta}
\end{aligned}$$
avec $\theta$ est un angle aigu.
- Appliquer l’identité : $\sin^2 \alpha+\cos^2 \alpha=1$ pour calculer $\cos\alpha,$ puis
utiliser la définition : $\tan \alpha=\dfrac{\sin \alpha}{\cos \alpha}$.
Corrigé 
-
- Calculons : $EF$ et $FG$.
Dans le triangle $EFG$ rectangle en $G$, pour l’angle $\widehat{GEF}$, on a :
$$\cos \widehat{GEF}=\dfrac{EG}{EF}=\dfrac{\sqrt{3}}{EF}$$
Or $$\cos \widehat{GEF}=\dfrac{\sqrt{3}}{3}$$
Donc : $$\dfrac{\sqrt{3}}{EF}=\dfrac{\sqrt{3}}{3}$$
D’où : $$\boxed{EF=3}.$$
Par Pythagore :
$$\begin{aligned}
EF^2&=EG^2+FG^2\\
FG^2&=EF^2-EG^2\\
FG^2&=3^2-\sqrt 3^2\\
FG^2&=9-3\\
FG^2&=6\\
FG&=\sqrt{6}.\quad (\text{car } FG > 0)\end{aligned}$$
Donc : $EF=3$ et $FG=\sqrt{6}$.
- On a le triangle $EFG$ est rectangle en $G$, alors :
$$\begin{aligned}
\sin\widehat{EFG}&=\dfrac{EG}{EF}=\dfrac{\sqrt{3}}{3},\\
\cos\widehat{EFG}&=\dfrac{FG}{EF}=\dfrac{\sqrt{6}}{3},\\
\tan\widehat{EFG}&=\dfrac{EG}{FG}=\dfrac{\sqrt{3}}{\sqrt{6}}=\dfrac{\sqrt{2}}{2}.\end{aligned}$$
-
- On connaît : $$\sin 30^\circ=\dfrac12,\ \sin 45^\circ=\dfrac{\sqrt{2}}{2},\ \cos 60^\circ=\dfrac12,\ \tan 60^\circ=\sqrt{3}.$$
Donc :
$$\begin{aligned}
U&=\sin 30^\circ-\sin 45^\circ-\cos 60^\circ+\tan 60^\circ\\
U&=\dfrac12-\dfrac{\sqrt{2}}{2}-\dfrac12+\sqrt{3}\\
U&=-\dfrac{\sqrt{2}}{2}+\sqrt{3}\\
U&=\sqrt{3}-\dfrac{\sqrt{2}}{2}.\end{aligned}$$
- On sait que :
$$\tan 15^\circ=\dfrac{1}{\tan 75^\circ}\text{ et } \cos 10^\circ=\sin 80^\circ.$$
Donc :
$$\begin{aligned}
V&=\tan 15^\circ-\dfrac{1}{\tan 75^\circ}-\cos 10^\circ+\sin 80^\circ\\
V&=\tan 15^\circ-\tan 15^\circ-\sin 80^\circ+\sin 80^\circ\\
V&=0\end{aligned}$$
- Comme $\alpha$ est aigu, $\cos\alpha>0$. Alors :
$$\begin{aligned}
\cos\alpha &=\sqrt{1-\sin^2\alpha}=\sqrt{1-\dfrac{1}{49}}\\
&=\sqrt{\dfrac{48}{49}}=\dfrac{\sqrt{48}}{7}=\dfrac{4\sqrt{3}}{7}.\end{aligned}$$
Et on a :
$$\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}
=\dfrac{\tfrac{1}{7}}{\tfrac{4\sqrt{3}}{7}}
=\dfrac{1}{4\sqrt{3}}
=\dfrac{\sqrt{3}}{12}.$$
Donc : $\displaystyle \cos\alpha=\dfrac{4\sqrt{3}}{7}\,\,$ et $\,\,\displaystyle \tan\alpha=\dfrac{\sqrt{3}}{12}$.
Enoncé 
Soient $A$, $B$, $C$, $D$ quatre points d’un cercle de centre $O$ tels que :
$\widehat{DOC}=100^\circ$ et $\widehat{DAB}=70^\circ$
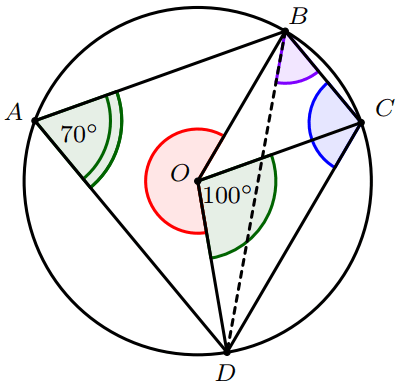
- Calculer la mesure de l’angle $\widehat{DBC}$
- Calculer la mesure de l’angle non convexe $\widehat{BOD}$
- Calculer la mesure de l’angle $\widehat{BCD}$
Indication 
-
Identifier l’angle au centre associé à l’angle inscrit $\widehat{DBC}$ et utiliser que la mesure d’un angle inscrit est égale à la moitié de celle de l’angle au centre interceptant le même arc.
-
Identifier l’angle au centre associé à l’angle inscrit $\widehat{DAB}$, calculer l’angle convexe au centre, puis utiliser que l’angle non convexe = $360^\circ$ – angle convexe.
-
Identifier l’angle non convexe au centre associé à l’angle inscrit $\widehat{BCD}$ et utiliser la propriété : un angle inscrit = moitié de l’angle au centre interceptant le même arc.
Corrigé 
-
Dans le cercle, $\widehat{DOC}$ est l’angle au centre associé à l’angle inscrit $\widehat{DBC}$, car ils interceptent le même arc $\overset{\frown}{DC}$.
Or, dans un cercle, la mesure d’un angle inscrit est égale à la moitié de la mesure de l’angle au centre associé.
Comme $\widehat{DOC}=100^\circ$, alors :
$$\widehat{DBC}=\dfrac{\widehat{DOC}}{2}=\dfrac{100^\circ}{2}=\boxed{50^\circ}$$
-
L’angle convexe $\widehat{DOB}$ est l’angle au centre associé à l’angle inscrit $\widehat{DAB}$, car ils interceptent le même arc $\overset{\frown}{DB}$.
Comme $\widehat{DAB}=70^\circ$, alors :
$$\widehat{DOB}=2\times\widehat{DAB}=2\times 70^\circ=140^\circ$$
Alors, la mesure de l’angle non convexe $\widehat{BOD}$ est :
$$\widehat{BOD}_{\text{non convexe}}=360^\circ-140^\circ=\boxed{220^\circ}$$
-
L’angle non convexe $\widehat{BOD}$ est l’angle au centre associé à l’angle inscrit $\widehat{BCD}$, car ils interceptent le même arc majeur $\overset{\frown}{BD}$.
Comme $\widehat{BOD}_{\text{non convexe}}=220^\circ$, alors :
$$\widehat{BCD}=\dfrac{\widehat{BOD}_{\text{non convexe}}}{2}=\dfrac{220^\circ}{2}=\boxed{110^\circ}$$
Enoncé 
On considère la figure suivante :
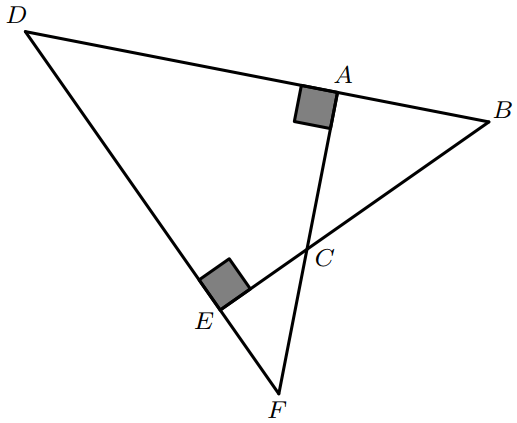
- Montrer que les triangles $BDE$ et $ADF$ sont semblables.
- Montrer que : $BD\times DA=DE\times DF$
- Montrer que les triangles $ACB$ et $ECF$ sont semblables.
Indication 
- Identifier deux angles égaux dans chaque triangle pour utiliser le 1er cas de similitude.
- Utiliser que si deux triangles sont semblables, alors les côtés homologues sont proportionnels.
- Comme la question 1 : identifier deux angles égaux pour utiliser le critère 1er cas de similitude.
Corrigé 
-
Les triangles $BDE$ et $ADF$ ont deux angles égaux :
– $\widehat{DAF} = \widehat{BED} = 90^\circ$
– $\widehat{ADE} = \widehat{BDE}$ (angles confondus).
Donc, par le 1er cas de similitude, les triangles $BDE$ et $ADF$ sont semblables.
-
Puisque les triangles $BDE$ et $ADF$ sont semblables, les longueurs des côtés homologues sont proportionnelles :
$$\frac{BD}{DF} = \frac{DE}{DA} = \frac{BE}{AF}$$
Donc :
$$\frac{BD}{DF} = \frac{DE}{DA}$$
En multipliant en croix, on obtient :
$$BD \times DA = DE \times DF$$
-
Les triangles $ACB$ et $ECF$ ont deux angles égaux :
– $\widehat{ACB} = \widehat{ECF}$ (angles opposés par le sommet).
– $\widehat{CAB} = \widehat{CEF}$ (angles droits).
Donc, par le 1er cas de similitude, les triangles $ACB$ et $ECF$ sont semblables.


















