ⓘ
Devoir surveillé n°2
Premier Semestre
Niveau : 3èm année collège
Leçons ciblées : Théorème de Thalèse, ordre et opérations.
Enoncé 
On considère la figure suivante tels que :
$\bullet$ $ABCD$ est un parallélogramme.
$\bullet$ $E$ un point de la droite $(AD)$ tel que : $AE=2$.
$\bullet$ $I$ est le point d’intersection des droites $(AB)$ et $(EC)$
$\bullet$ $M$ un point du segment $[DC]$ tel que : $DM=2,8$
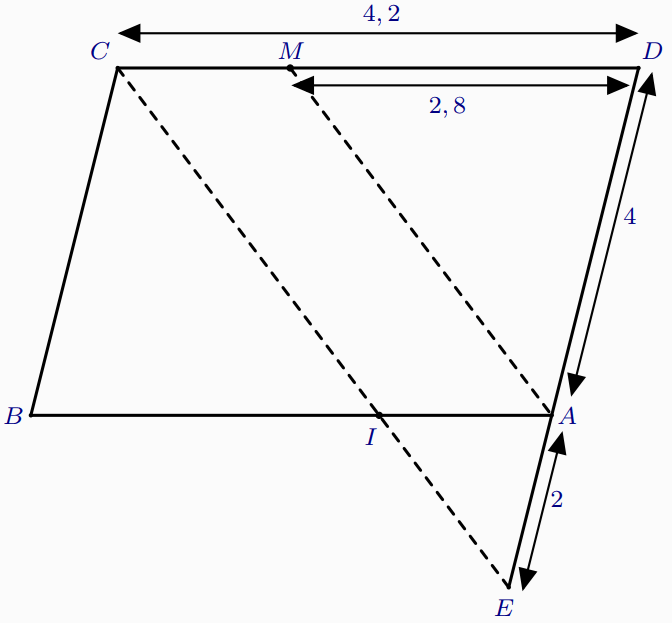
- Montrer que : $AI=1,4$.
(3pts)
- Montrer que : $IC=2IE$.
(2pt
- Montrer que : $\left( AM\right)\parallel \left( EC\right)$
(3pts)
- Montrer que : $3 \times AM =2 \times CE$
(2pts)
Indication 
- Appliquer le théorème de Thalès sur le triangle $ECD$.
Identifier les points $A \in (ED)$ et $I \in (EC)$, et utiliser que $(AI) \parallel (DC)$ pour établir le rapport.
- Appliquer le théorème de Thalès sur le triangle $IBC$.
- Vérifier les rapports $\dfrac{DA}{DE}$ et $\dfrac{DM}{DC}$, puis appliquer la réciproque du théorème de Thalès sur le triangle $EDC$.
- Appliquer le théorème de Thalès sur le triangle $DEC$.
Corrigé 
- Dans le triangle $EDC$ :
$A \in (ED)$, $I \in (EC)$ et $(AI)\parallel(DC)$
Donc, d’après le théorème de Thalès :
$$\frac{EA}{ED}=\frac{EI}{EC}=\frac{AI}{DC}$$ Ainsi :
$$\frac{2}{6}=\frac{AI}{4,2}$$ alors : $$AI=\frac{2\times 4,2}{6}=\frac{8,4}{6}=1,4$$ Donc : $$\boxed{AI = 1,4}.$$
- Dans le triangle $IBC$ :
$A\in (IB)$, $E\in (IC)$ et $(AE)\parallel (BC)$
D’après le théorème de Thalès :
$$\frac{IC}{IE}=\frac{IB}{IA}=\frac{BC}{AE}$$ On en déduit :
$$\frac{IC}{IE}=\frac{BC}{AE}=\frac{4}{2}=2$$ Donc : $$\boxed{IC=2\,IE}$$
- Dans le triangle $DEC$, on a : $A\in(DE)$, $M\in(DC)$.Les points $D,A,E$ ainsi que $D,M,C$ sont dans le même ordre.On compare les deux rapports : $$\dfrac{DA}{DE} \quad\text{ et }\quad\dfrac{DM}{DC}$$
On a :
$$\frac{DA}{DE}=\frac{4}{6}=\frac{2}{3}, \quad \frac{DM}{DC}=\frac{2,8}{4,2}=\frac{28}{42}=\frac{2}{3}$$ Donc : $$\frac{DA}{DE}=\frac{DM}{DC}$$ Par la réciproque du théorème de Thalès, on conclut :
$$\boxed{(AM)\parallel(EC)}$$
- Dans le triangle $DEC$ :
$A\in(DE)$, $M\in(DC)$ et $(AM)\parallel(EC)$.
Donc :
$$\frac{DA}{DE}=\frac{DM}{DC}=\frac{AM}{CE}$$ En particulier :
$$\frac{DA}{DE}=\frac{AM}{CE}$$ Remplaçons :
$$\frac{4}{6}=\frac{AM}{CE}$$ alors : $$\frac{2}{3}=\frac{AM}{CE}$$ D’où la relation :
$$\boxed{3AM=2CE}$$
Enoncé 
-
- Comparer : $\sqrt{19}$ et $3\sqrt{2}$(1.5pts)
- En déduire la simplification de $K$ tel que : $K=\sqrt{\Big( 3\sqrt{2}-\sqrt{19}\Big)^2}+3\sqrt{2}$(1pt)
-
- Comparer : $-3\sqrt{5}$ et $-4\sqrt{3}$(1.5pts)
- En déduire la comparaison des nombres : $\dfrac{1}{2025+3\sqrt{5}}$ et $\dfrac{1}{2025+4\sqrt{3}}$(1pt)
Indication 
-
- Les deux nombres sont positifs. Compare leurs carrés : $ (\sqrt{19})^2 $ et $ (3\sqrt{2})^2 $.
- Déduis le signe de $3\sqrt{2}-\sqrt{19}$ grâce à (a). Puis utilise
$ \sqrt{(x)^2}=-x $, si $x<0$. Simplifie ensuite.
-
- Compare $3\sqrt{5}$ et $4\sqrt{3}$ en comparant leurs carrés. Ensuite, multiplie l’inégalité par $-1$ (le sens s’inverse).
- Ajoute $2025$ aux deux membres de l’inégalité obtenue en (a). Comme les dénominateurs sont positifs, utilise la règle : si $0 < a < b$, alors $\dfrac{1}{a} > \dfrac{1}{b}$.
Corrigé 
-
- On compare les carrés (quantités positives) :
$$\big(\sqrt{19}\big)^2=19 \quad\text{et}\quad \big(3\sqrt{2}\big)^2=9\times2=18.$$ Comme $19>18$, on a :
$$\boxed{\sqrt{19} \;>\; 3\sqrt{2}}.$$
- D’après (a), $\sqrt{19} \;>\; 3\sqrt{2}$, alors : $3\sqrt{2}-\sqrt{19}<0$, alors :
\[\begin{aligned}
K &= \sqrt {{{\left( {3\sqrt 2 – \sqrt {19} } \right)}^2}} + 3\sqrt 2 \\
K &= – \left( {3\sqrt 2 – \sqrt {19} } \right) + 3\sqrt 2 \\
K &= – 3\sqrt 2 + \sqrt {19} + 3\sqrt 2 \\
K &= \sqrt {19}
\end{aligned}\]
D’où :
$$\boxed{K=\sqrt{19}}.$$
-
- On compare d’abord $3\sqrt{5}$ et $4\sqrt{3}$ (positifs) :
$$\big(3\sqrt{5}\big)^2=9\times5=45,\qquad \big(4\sqrt{3}\big)^2=16\times3=48.$$ Donc : $$3\sqrt{5}<4\sqrt{3}.$$ En multipliant par $-1$ (ce qui inverse le sens) : $$\boxed{-3\sqrt{5}\;>\;-4\sqrt{3}}.$$
- D’après (a), $3\sqrt{5}<4\sqrt{3}$, donc :
$$2025+3\sqrt{5}\;<\;2025+4\sqrt{3}.$$ Pour des dénominateurs positifs, plus le dénominateur est petit, plus la fraction est grande. Ainsi : $$\boxed{\dfrac{1}{2025+3\sqrt{5}} \;>\; \dfrac{1}{2025+4\sqrt{3}}}.$$
Enoncé 
Soient $a$, $b$ et $c$ trois nombres réels tels que :
$1 \le a \le 3$, $-6 \le b \le -2$ et $1 \le \sqrt {5 -c} \le 2$
- Encadrer : $a+b$
(1pt)
- Encadrer : $a-b$
(1.5pts)
- Montrer que : $0 \le \dfrac{{ab + 18}}{{16}} \le 1$
(1.5pts)
- Montrer que : $1 \le c \le 4$
(1pt)
Indication 
Solution organisée — Encadrements
On donne les informations suivantes :
- $1 \le a \le 3$
- $-6 \le b \le -2$
- $1 \le \sqrt{5-c} \le 2$
Nous encadrons successivement les expressions demandées.
- Encadrer $a+b$.
Puisque $1\le a\le3$ et $-6\le b\le -2$, on additionne les bornes correspondantes :
$$1+(-6) \le a+b \le 3+(-2)$$
d’où
$$-5 \le a+b \le 1$$
- Encadrer $a-b$.
Remarquez que $-b$ est l’opposé de $b$. Comme $-6\le b\le -2$, on a
$$2 \le -b \le 6$$
En ajoutant les inégalités $1\le a\le3$ et $2\le -b\le6$ terme à terme :
$$1+2 \le a+(-b) \le 3+6$$
soit
$$3 \le a-b \le 9$$
- Encadrer $\dfrac{ab+18}{16}$.
On utilise encore $1\le a\le3$ et $2\le -b\le6$, donc
$$1 \times 2 \le a \times (-b) \le 3 \times 6$$
Cela donne :
$$2 \le -ab \le 18 \quad \Longrightarrow \quad -18 \le ab \le -2$$
En ajoutant $18$ à chaque membre :
$$-18+18 \le ab+18 \le -2+18 \quad \Longrightarrow \quad 0 \le ab+18 \le 16$$
Enfin, en divisant par $16>0$ :
$$0 \le \dfrac{ab+18}{16} \le 1$$
- Encadrer $c$.
On a $1 \le \sqrt{5-c} \le 2$. En élevant au carré :
$$1^2 \le 5-c \le 2^2 \quad \Longrightarrow \quad 1 \le 5-c \le 4$$
Isolons $c$ :
$$1-5 \le -c \le 4-5 \quad \Longrightarrow \quad -4 \le -c \le -1$$
En multipliant par $-1$ :
$$1 \le c \le 4$$
Récapitulatif :
- $-5 \le a+b \le 1$
- $3 \le a-b \le 9$
- $0 \le \dfrac{ab+18}{16} \le 1$
- $1 \le c \le 4$
Corrigé 
- Puisque : $1 \le a \le 3$ et $-6 \le b \le -2$, on additionne les bornes correspondantes :
alors : $$1+(-6) \le a+b \le 3+(-2),$$ alors : $$\boxed{-5 \le a+b \le 1}$$
- Remarquez que $-b$ est l’opposé de $b$. Comme $-6\le b\le -2$, on a
$$2 \le -b \le 6$$
En ajoutant les inégalités $1\le a\le3$ et $2\le -b\le6$ terme à terme :
$$1+2 \le a+(-b) \le 3+6$$ d’où :
$$\boxed{3 \le a-b \le 9}$$
- On utilise encore $1\le a\le3$ et $2\le -b\le6$, donc :
$$1 \times 2 \le a \times (-b) \le 3 \times 6$$
Cela donne :
$$2 \le -ab \le 18$$
donc :
$$-18 \le ab \le -2$$
En ajoutant $18$ à chaque membre :
$$-18+18 \le ab+18 \le -2+18$$
c’est-à-dire :
$$0 \le ab+18 \le 16$$
Enfin, en divisant par $16>0$ :
$$\boxed{0 \le \dfrac{ab+18}{16} \le 1}$$
- On a : $1 \le \sqrt {5 -c} \le 2$. En élevant au carré :
$$1^2 \le \sqrt {5 -c}^2 \le 2^2$$
C’est-à-dire :
$$1 \le 5 -c \le 4$$
Isolons $c$ :
$$1-5 \le -c \le 4-5$$
C’est-à-dire :
$$-4 \le -c \le -1$$
En multipliant par $-1$ :
$$\boxed{1 \le c \le 4}$$












