Cours : Vecteurs et translation – 3ac

Égalité de deux vecteurs

Définition : Deux vecteurs sont égaux s’ils ont :

La même direction.
Le même sens.
La même longueur (norme).

Exemple :

Figure 1. Egalité de deux vecteurs

Dans les deux cas ci-dessus, les deux vecteurs $\overrightarrow {AB}$ et $\overrightarrow {CD}$ ont :

La même direction : $\left( {AB\,} \right)\,\parallel \,\,\left( {CD} \right)$.
Le même sens : $A$ vers $B$.
La même norme : $AB=CD$.

On écrit : $\overrightarrow {AB} \,\, = \,\,\overrightarrow {CD} $

Propriété : Soient $A$, $B$, $C$ et $D$ quatre points distincts (non alignés).

$\overrightarrow {AB} \,\, = \,\,\overrightarrow {CD} $ si et seulement si $ABDC$ est un parallélogramme.

Remarques :

$\overrightarrow {AA} = \overrightarrow {BB} = …… = \,\,\overrightarrow 0 $ est appelé le vecteur nul.
Si $\overrightarrow {AB} \,\, = \,\,\overrightarrow 0 $ alors $A=B$.
Le vecteur $\overrightarrow {BA} \,$ est l’opposé du vecteur $\overrightarrow {AB}. \,$

On écrit : $\overrightarrow {AB} = – \overrightarrow {BA} \,$

Somme de deux vecteurs

Définition : La somme des vecteurs $\overrightarrow {AB}$ et $\overrightarrow {AC}$ est le vecteur $\overrightarrow {AD}$ tel que $ABDC$ est un parallélogramme.

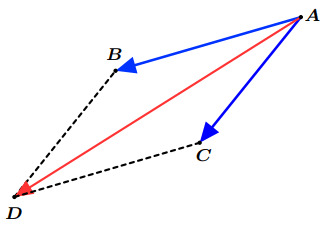
Figure 2: Somme de deux vecteurs

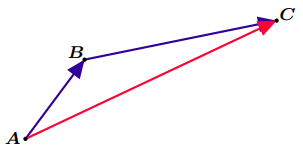
Relation de Chasles : Pour tous points $A$, $B$ et $C$ : $$\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} $$

Figure 3: Relation de Chasles

Produit d’un vecteur par un nombre réel

Définition : Soient $A$, $B$ et $M$ trois points, et $\alpha$ un nombre réel non nul.
Le vecteur $\overrightarrow {AM}$ est le produit de $\overrightarrow {AB}$ par $\alpha$ signifie que : $\overrightarrow {AM} = \alpha \overrightarrow {AB} $

Si $\alpha>0$ alors $\overrightarrow {AM}$ et $\overrightarrow {AB}$ ont le même sens, et $AM=\alpha AB$.
Si $\alpha<0$ alors $\overrightarrow {AM}$ et $\overrightarrow {AB}$ sont de sens contraires, et $AM=-\alpha AB$.

Remarque :

$\alpha \times \overrightarrow 0 = \overrightarrow 0 $
$0 \times \overrightarrow {AB} = \overrightarrow 0 $

Exemples :

Soit $\overrightarrow{AB}$ un vecteur, construire le point $M$ tel que $\overrightarrow {AM} = 4\overrightarrow {AB} $
On a: $\overrightarrow {AM} = 4\overrightarrow {AB} $ signifie que :
$\quad\quad\bullet\quad M \in \left( {AB} \right)$,
$\quad\quad\bullet\quad \overrightarrow {AM}$ et $\overrightarrow {AB}$ ont le même sens,
$\quad\quad\bullet\quad AM=4AB$

Figure 4: Produit d’un vecteurs par un nombre positif
Soit $\overrightarrow{AB}$ un vecteur, construire le point $N$ tel que $\overrightarrow {AN} = -5\overrightarrow {AB} $
On a: $\overrightarrow {AN} = -\overrightarrow {AB} $ signifie que :
$\quad\quad\bullet\quad N \in \left( {AB} \right)$,
$\quad\quad\bullet\quad\overrightarrow {AN}$ et $\overrightarrow {AB}$ sont de sens contraires,
$\quad\quad\bullet\quad AN=5AB$

Figure 5: Produit d’un vecteurs par un nombre négatif

Propriétés:

$\overrightarrow {AM} = \alpha \overrightarrow {AB} $, alors les points $A$, $M$, $B$ sont alignés.
Si $\overrightarrow {MN} = \alpha \overrightarrow {AB} $, alors les droites $(MN)$ et $(AB)$ sont parallèles.

Propriété (Milieu d’un segment) :
Si le point $M$ est le milieu du segment $[AB]$ alors :
$\quad\bullet\quad\overrightarrow {MA} = – \overrightarrow {MB} $
$\quad\bullet\quad\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 $
$\quad\bullet\quad\overrightarrow {AM} = \overrightarrow {MB} = \dfrac{1}{2}\overrightarrow {AB} $

Translation

Image d’un point par une translation

Définition:
Le point $M’$ est l’image de $M$ par la translation du vecteur $\overrightarrow {AB} $, signifie que : $\overrightarrow {MM’} = \overrightarrow {AB} $

Remarque:
On dit aussi que $M’$ est l’image de $M$ par la translation qui transforme $A$ en $B$.

Exemple:

Figure 6: Image d’un point par une translation

Dans les deux cas ci-dessus, $M’$ est l’image de $M$ par la translation du vecteur $\overrightarrow {AB} $

Propriété: Soient $M$ et $N$ deux points du plan.
Si $M’$ et $N’$ sont les images respectives des points $M$ et $N$ par une translation du vecteur $\overrightarrow {u}$, alors : $\overrightarrow {M’N’} =\overrightarrow {MN} $
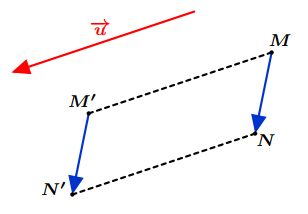
Images de deux points par une translation

Figure 7: Images de deux points par une translation

Image d’un segment par une translation

Propriété: On considère la translation du vecteur $\overrightarrow {u}$
L’image du segment $[MN]$ par la translation du vecteur $\overrightarrow {u}$ est le segment $[M’N’]$, et on a : $M’N’=MN$.
On dit que : la translation conserve les longueurs.
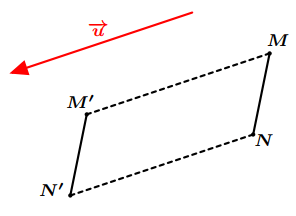
Image d'un segment par une translation

Figure 8: Image d’un segment par une translation

Image d’une droite, demi-droite, points alignés

Propriété: On considère la translation du vecteur $\overrightarrow {u}$
$\bullet$ L’image de la droite $(MN)$ par la translation du vecteur $\overrightarrow {u}$ est la droite $(M’N’)$, et on a : $(M’N’)\parallel (MN)$

On dit que : la translation conserve l’alignement des points

$\bullet$ L’image de la demi-droite $[MN)$ par la translation du vecteur $\overrightarrow {u}$ est la demi-droite $[M’N’)$.

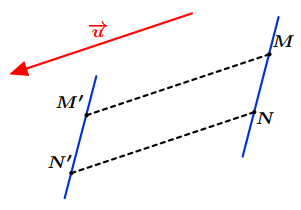
Figure 9: Image d’une droite par une translation

Image d’un angle par une translation

Propriété : On considère la translation du vecteur $\overrightarrow {u}$
L’image de l’angle $\widehat{AOB}$ par la translation du vecteur $\overrightarrow {u}$ est l’angle $\widehat{A’O’B’}$, et on a : $\widehat{AOB}=\widehat{A’O’B’}$

On dit que: la translation conserve la mesure d’angles.

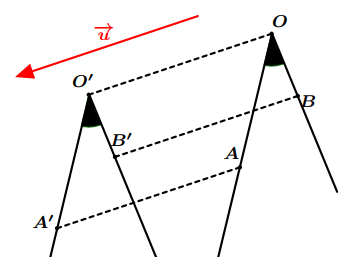
Figure 10: Image d’un angle par une translation

Image d’un cercle par une translation

Propriété: On considère la translation du vecteur $\overrightarrow {u}$

L’image du cercle $(\mathcal{C})$ de centre $O$ et de rayon $r$ par la translation du vecteur $\overrightarrow {u}$ est le cercle $(\mathcal{C}’)$ de centre $O’$ et de même rayon $r$.

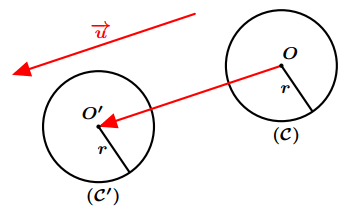
Figure 11: Images d’un cercle par une translation