Chapitre 7

Cosinus, sinus et tangente d’un angle aigu

Cosinus d’un angle aigu

Définition : Soit

$\hat B$ un angle aigu dans un triangle rectangle.

$\cos \hat B= \dfrac{\text{longueur du côté adjacent à }\hat B}{\text{longueur de l’hpoténuse }}$

Exemple : Soit $ABC$ un triangle rectangle en $A$ .

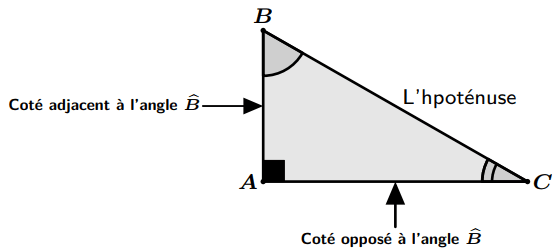
Trigonométrie

On a : $\boxed{\cos \widehat {ABC} = \frac{{AB}}{{BC}}}$ et $\boxed{\cos \widehat {ACB} = \frac{{AC}}{{BC}}}$

Sinus d’un angle aigu

Définition : Soit

$\hat B$ un angle aigu dans un triangle rectangle.

$\sin \hat B= \dfrac{\text{longueur du côté opposé à }\hat B}{\text{longueur de l’hpoténuse }}$

Exemple : Soit $ABC$ un triangle rectangle en $A$ .

Trigonométrie

On a : $\boxed{\sin \widehat {ABC} = \frac{{AC}}{{BC}}}$ et $\boxed{\sin \widehat {ACB} = \frac{{AB}}{{BC}}}$

Tangente d’un angle aigu

Définition : Soit

$\hat B$ un angle aigu dans un triangle rectangle.

$\tan \hat B= \dfrac{\text{longueur du côté opposé à }\hat B}{\text{longueur du côté adjacent}\hat B}$

Exemple : Soit $ABC$ un triangle rectangle en $A$ .

Trigonométrie

On a : $\boxed{\tan \widehat {ABC} = \frac{{AC}}{{AB}}}$ et $\boxed{\tan \widehat {ACB} = \frac{{AB}}{{AC}}}$

Formules trigonométries

Propriété 1 : Si

$\alpha$ est la mesure d’un angle aigu

$\left( {0^\circ < \alpha < 90^\circ } \right)$ , alors :

$0 < \cos \,\alpha \, < \,1$
$0 < \sin \,\alpha \, < \,1$
${\cos ^2}\,\alpha \,\, + \,\,{\sin ^2}\,\alpha \,\, = \,\,1$

Preuve :

$\bullet$ Soit $ABC$ un triangle rectangle en $A$ . On pose $\alpha=\widehat {ABC}$

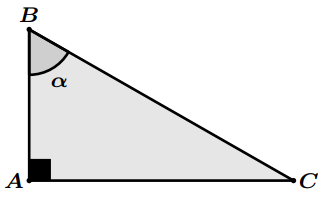
Trigonometrie2

On a : $\sin \alpha= \dfrac{{AC}}{{BC}}$ et $\cos \alpha= \dfrac{{AB}}{{BC}}$

Nous savons que le plus long côté d’un triangle rectangle est l’hypoténuse,

C’est-à-dire : $0<AB<BC$ et $0<AC<BC$ ,

donc : $\dfrac{0}{BC}<\dfrac{AC}{BC}<\dfrac{BC}{BC}$ et $\dfrac{0}{BC}<\dfrac{AB}{BC}<\dfrac{BC}{BC}$

c’est-à-dire : $0<\sin \alpha<1$ et $0<\cos\alpha<1$ .

$\bullet$ D’après le théorème de Pythagore, on a : $AC^2+AB^2=BC^2$ ,

Par suite, on a :
$\begin{aligned} {\sin ^2}\alpha + {\cos ^2}\alpha &= {\left( {\frac{{AC}}{{BC}}} \right)^2} + {\left( {\frac{{AB}}{{BC}}} \right)^2}\\ &= \frac{{A{C^2} + A{B^2}}}{{B{C^2}}}\\ &= \frac{{B{C^2}}}{{B{C^2}}}\\ &= 1 \end{aligned}$

Remarque 1 : Si

$\alpha$ est la mesure d’un angle aigu

$\left( {0^\circ < \alpha < 90^\circ } \right)$ , alors :

${\cos ^2}\alpha = 1-\sin^2 \alpha$
${\sin ^2}\alpha = 1-\cos^2 \alpha$

Propriété 2 : Si

$\alpha$ est la mesure d’un angle aigu

$\left( {0^\circ < \alpha < 90^\circ } \right)$ , alors :

${\tan}\alpha = \dfrac{\sin \alpha}{\cos \alpha}$

Remarque 2 : Si

$\alpha$ est la mesure d’un angle aigu

$\left( {0^\circ < \alpha < 90^\circ } \right)$ , alors :

${\cos}\alpha = \dfrac{\sin \alpha}{\tan \alpha}$
${\sin}\alpha = \cos\alpha\times\tan \alpha$

Propriété 3 : Si

$\alpha$ et

$\beta$ sont les mesures de deux angles complémentaires

$\left( {\alpha+\beta = 90^\circ } \right)$ , alors :

$\cos \alpha = \sin \beta$
$\sin \alpha = \cos \beta$
$\tan \alpha = \dfrac{1}{\tan\beta}$

Remarque 3 : Si

$\alpha$ est la mesure d’un angle aigu

$\left( {0^\circ < \alpha < 90^\circ } \right)$ , alors :

$\cos\left( {90^\circ – \alpha } \right)= \sin\alpha$
$\sin\left( {90^\circ – \alpha } \right) = \cos \alpha$
$\tan\left( {90^\circ – \alpha } \right) = \dfrac{1}{\tan\alpha}$

Angles particuliers

$x$	$0^\circ$	$30^\circ$	$45^\circ$	$60^\circ$	$90^\circ$
$\sin x$	$0$	$\dfrac{1}{2}$	$\dfrac{\sqrt 2}{2}$	$\dfrac{\sqrt 3}{2}$	$1$
$\cos x$	$1$	$\dfrac{\sqrt 3}{2}$	$\dfrac{\sqrt 2}{2}$	$\dfrac{\sqrt 1}{2}$	$0$
$\tan x$	$0$	$\dfrac{\sqrt 3}{3}$	$1$	$\sqrt 3$	$***$