Chapitre 4
Théorème de Thalès
Théorème 1 : Soient $(d_1)$ et $(d_2)$ deux droites sécantes en $A$.
$B$ et $M$ deux points de la droite $(d_1)$, distincts de $A$.
$C$ et $N$ deux points de la droite $(d_2)$, distincts de $A$.
Si les droites $(BC)$ et $(MN)$ sont parallèles alors : $$\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC}$$
$B$ et $M$ deux points de la droite $(d_1)$, distincts de $A$.
$C$ et $N$ deux points de la droite $(d_2)$, distincts de $A$.
Si les droites $(BC)$ et $(MN)$ sont parallèles alors : $$\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC}$$
Il y a trois configurations correspondantes à ce théorème.
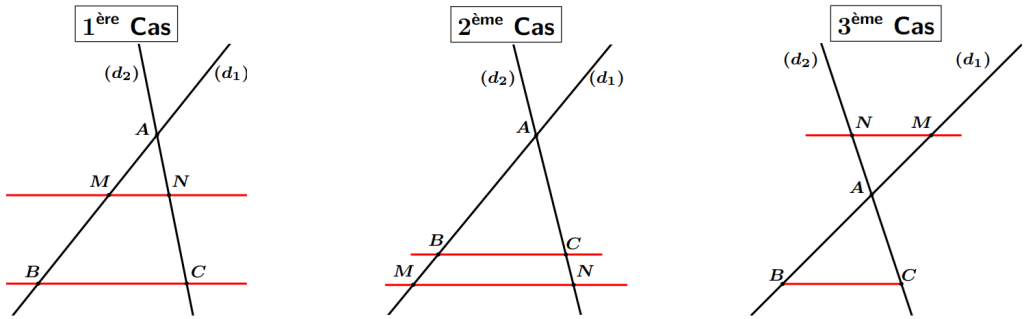
Remarque :
- Les points $A$, $B$, $M$ et $A$, $C$, $N$ sont alignés dans le même ordre.
- Le théorème de Thalès permet de calculer les longueurs.
Réciproque du théorème de Thalès
Théorème 2 : Soient $(d_1)$ et $(d_2)$ deux droites sécantes en $A$.
$B$ et $M$ deux points de la droite $(d_1)$, distincts de $A$.
$C$ et $N$ deux points de la droite $(d_2)$, distincts de $A$.
Si les $A$, $B$, $M$ et $A$, $C$, $N$ sont alignés dans le même ordre et $\dfrac{AM}{AB}=\dfrac{AN}{AC}$, alors les droites $(MN)$ et $(BC)$ sont parallèles.
$B$ et $M$ deux points de la droite $(d_1)$, distincts de $A$.
$C$ et $N$ deux points de la droite $(d_2)$, distincts de $A$.
Si les $A$, $B$, $M$ et $A$, $C$, $N$ sont alignés dans le même ordre et $\dfrac{AM}{AB}=\dfrac{AN}{AC}$, alors les droites $(MN)$ et $(BC)$ sont parallèles.
Il y a deux configurations correspondantes à ce théorème.

Remarque :
- L’hypothèse « alignés dans le même ordre » est essentielle.
- La réciproque du théorème de Thalès permet de démontrer le parallélisme de deux droites.
Exemple : On considère la figure suivante:
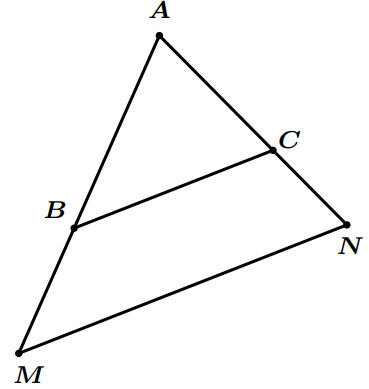
On donne : $AB=35cm$; $AM=40cm$; $AC=21cm$ ; $AN=24cm$
On a : $\dfrac{AM}{AB}=\dfrac{40}{35}=\dfrac{8}{7}$ et $\dfrac{AN}{AC}=\dfrac{24}{21}=\dfrac{8}{7}$, alors : $\dfrac{AM}{AB}=\dfrac{AN}{AC}$.
Et on sait que les points $A$, $B$, $M$ et $A$, $C$, $N$ sont alignés dans le même ordre.
Alors on peut conclure que les droites (BC) et $(MN)$ sont parallèles.





