Coordonnées d’un point
Définition: Le plan est muni d’un repère orthonormé $(O;I;J)$.
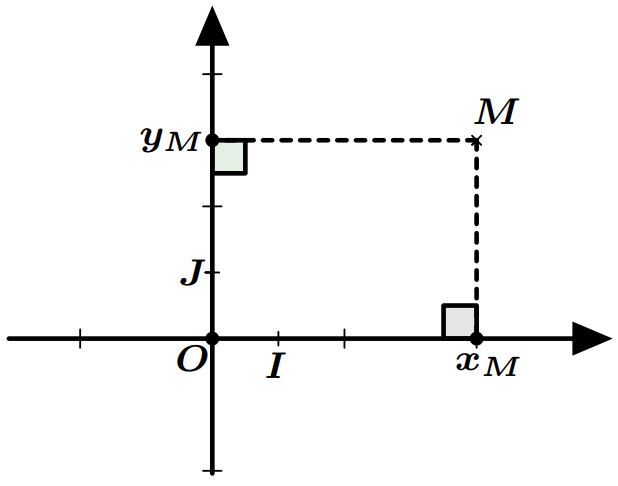
- Le couple $(x_M;y_M)$ s’appelle le couple de coordonnées de $M$. On écrit $M(x_M;y_M)$.
- Le nombre $x_M$ s’appelle abscisse du point $M$.
- Le nombre $y_M$ s’appelle ordonnée du point $M$.
- Le point $O$ s’appelle origine du repère.
- La droite $(OI)$ s’appelle l’axe des abscisses.
- La droite $(OJ)$ s’appelle l’axe des ordonnées.

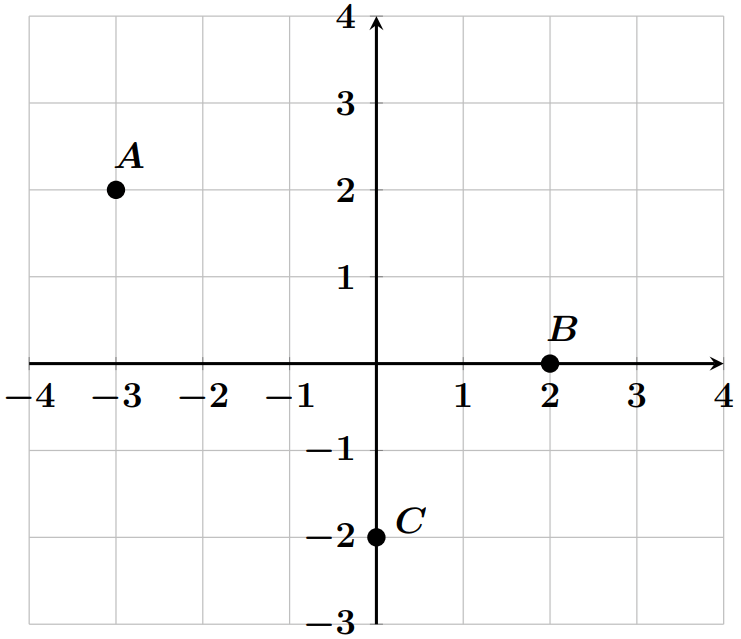
Exemple : Sur la figure suivante, les coordonnées des $A$, $B$ et $C$: $$A(-3;2);\quad B(2;0);\quad C(0;-2)$$
Coordonnées d’un vecteur
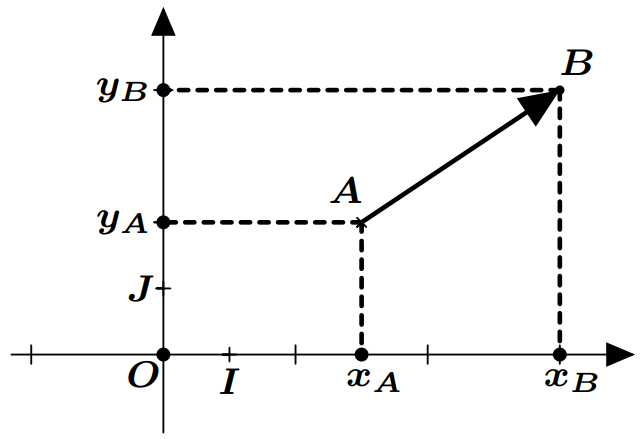
Propriété: Dans un repère, si deux points $A(x_A;y_A)$ et $B(x_B;y_B)$, alors le vecteur $\overrightarrow {AB}$ a pour coordonnées $\left( {{x_B} – {x_A};{y_B} – {y_A}} \right)$. On écrit : $\overrightarrow {AB} \left( {{x_B} – {x_A};{y_B} – {y_A}} \right)$

Exemple : On donne : $A(-3;4)$ et $B(-2;-1)$, alors on a : $$\begin{aligned}
& x_B-x_A=-2-(-3)=1\\
& y_B-y_A=-1-4=-5
\end{aligned}$$ Donc : $\boxed{\overrightarrow {AB}(1;-5)}$
Égalité de deux vecteurs
Propriété: Deux vecteurs sont égaux signifie qu’ils ont les mêmes coordonnées.
Autrement dit: $\overrightarrow {AB} = \overrightarrow {CD}$ signifie que : $x_B-x_A=x_D-x_C$ et $y_B-y_A=y_D-y_C$.
Coordonnées de la somme de deux vecteurs
Propriété: Si $\overrightarrow {AB}(a,b)$ et $\overrightarrow {CD}(c,d)$, alors :
$$\overrightarrow {AB}+\overrightarrow {CD}(a+c;b+d)$$
$$\overrightarrow {AB}+\overrightarrow {CD}(a+c;b+d)$$
Exemple : On donne $\overrightarrow {AB}(-4,-2)$ et $\overrightarrow {CD}(6,-3)$,
donc : $\overrightarrow {AB}+\overrightarrow {CD}(-4+6;-2-3)$,
donc : $\overrightarrow {AB}+\overrightarrow {CD}(2;-5)$
Coordonnées du milieu d’un segment
Propriété : Soit $A(x_A;y_A)$ et $B(x_B;y_B)$ deux points dans un repère.
Si $M$ est le milieu de $[AB]$, alors : $$x_M=\dfrac{x_A+x_B}{2}\quad\text{ et }\quad y_M=\dfrac{y_A+y_B}{2}$$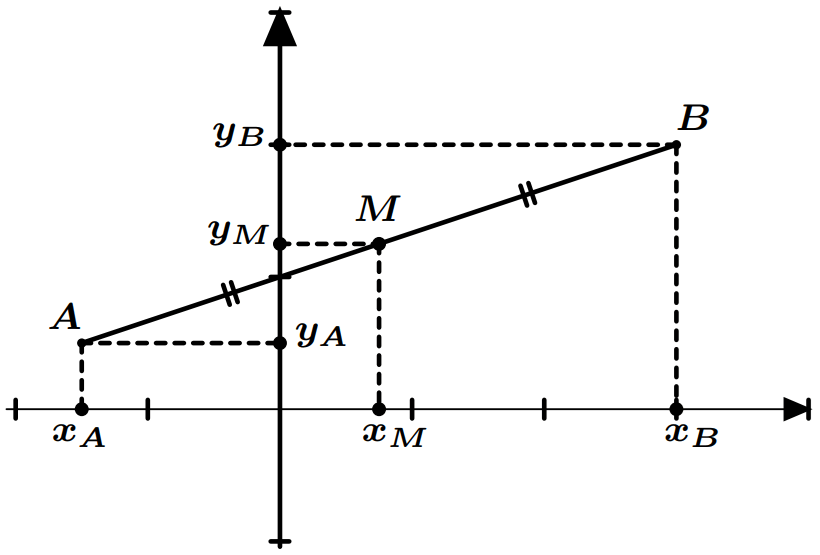
Si $M$ est le milieu de $[AB]$, alors : $$x_M=\dfrac{x_A+x_B}{2}\quad\text{ et }\quad y_M=\dfrac{y_A+y_B}{2}$$

Distance de deux points dans un repère orthonormé
Propriété : Soit $A(x_A;y_A)$ et $B(x_B;y_B)$ deux points dans un repère, alors : $$AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$$





