Cours : Notions de géométrie – 1ac

Droite

Propriété :

Par deux points distincts $A$ et $B$, passe une et une seule droite, on la note: $(A B)$ ou $(B A)$.
Si $M$ est un point de la droite $(A B)$, alors on note $M \in(A B)$ et se lit: $M$ appartient à la droite $(A B)$.

Remarques :

Une droite est illimitée des deux côtés.
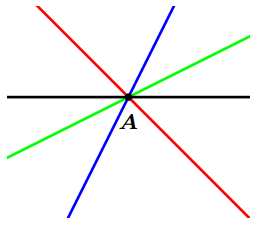
Par un point, passe une infinité de droites.
Tous les points qui appartiennent à la même droite, sont des points alignés.

Les points $A, B, C$ et $E$ sont alignés.

Demi-droite

Définition : Soit $(D)$ une droite. $A, B$ et $C$ sont des points de la droite $(D)$.

La partie de la droite $(D)$ coloriée en rouge, limitée par le point $A$, et passant par le point $B$ est appelée: La demi-droite d’origine $A$, et qui passe par le point $B$. On la note: $[A B)$
La partie de la droite $(D)$ coloriée en vert est la demi-droite $[A C)$

Segment-Milieu d’un segment

Définition : Soit $(D)$ une droite passant par les points $A$ et $B$.

Le segment d’extrémités $A$ et $B$ noté $[A B]$ ou $[B A]$ est la partie coloriée en bleu. ( $A$ et $B$ font parties du segment)

Définition : Le milieu d’un segment est le point de ce segment, qui se situe à la même distance des deux extrémités du segment.

Autrement dit: $M$ milieu de $[A B]$ signifie que : $M$ appartient à $[A B]$ et $M A=M B$

Positions relatives de deux droites

Droites sécantes

Définition :

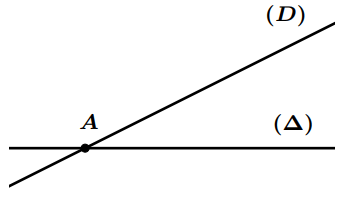
Deux droites $(D)$ et $(\Delta)$ qui se coupent en un seul point, sont appelées droites sécantes.
On dit aussi que les droites $(D)$ et $(\Delta)$ sont sécantes en $A$

Droites parallèles

Définition : Deux droites $(D)$ et $(\Delta)$ qui ne se coupent pas, sont appelées droites parallèles et on note: $(D) / /(\Delta)$

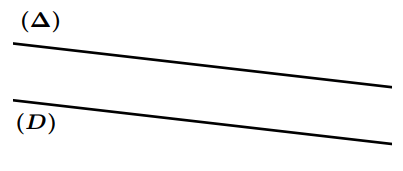
Remarque : Deux droites confondues sont aussi parallèles.

Droites perpendiculaires

Définition : Deux droites $(D)$ et $(\Delta)$ sont perpendiculaires, et on note $(\Delta) \perp(D)$ si elles sont sécantes et forment quatre angles droits.

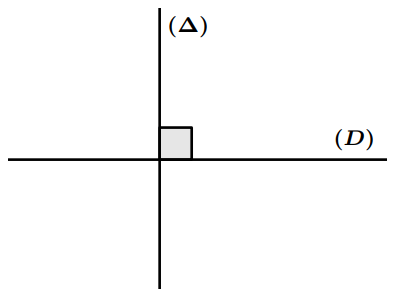
Définition : Soit $(D)$ et $(\Delta)$ deux droites perpendiculaires en $H$; et soit $M$ un point de la droite $(D)$.

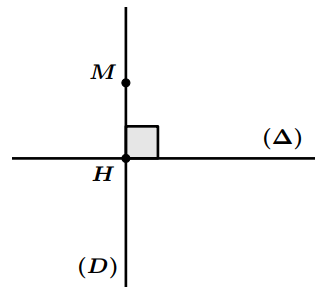
Projection orthogonale du point A sur une droite.

Le point $H$ est appelé le projeté orthogonal du point $M$ sur la droite ($\Delta$)
La longueur $M H$ est appelée la distance du point $M$ à la droite ($\Delta$)

Propriétés :

Propriétés :

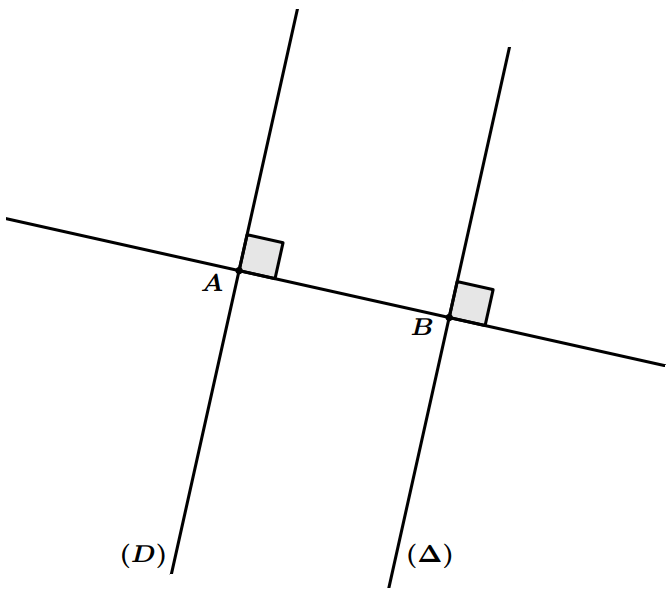
Si deux droites sont parallèles, alors toute droite perpendiculaire à lune est perpendiculaire à l’autre.
Si deux droites sont parallèles, alors toute droite parallèle à l’une est parallèle à l’autre,
Si deux droites sont perpendiculaires, alors toute droite perpendiculaire à lune est parallèle à l’autre.
Si deux droites sont perpendiculaires, alors toute droite parallèle à l’une est perpendiculaire à l’autre.

Exemple : Dans la figure ci-dessous, on a : $(D)\perp (AB)$ et $(\Delta)\perp (AB)$, donc : $(D)\parallel (\Delta)$

Illustration de deux droites perpendiculaires sur une même droite.