Fonction linéaire
La relation $f$ qui, à tout nombre réel $x$, associe le produit $ax$, est appelée fonction linéaire de coefficient $a$.
On la note : $$f : x \mapsto ax$$ Le nombre $ax$ est l’image de $x$ par $f$, et on écrit : $f(x)=ax$, $\quad \Big(f(x)$ se lit « $f$ de $x$ »$\Big)$.
Exemple :
Le périmètre d’un triangle équilatéral est proportionnel à la longueur de son côté.
Soit $x$ la longueur du côté, alors le périmètre de ce triangle est : $3x$.
Ainsi, on définit la fonction linéaire $p$ telle que : $p(x) = 3x$
L’image de $4$ par $p$ se note $p(4)$ :
$$p(4) = 3 \times 4 = 12$$
Donc, $12$ est l’image de $4$ par la fonction linéaire $p$.
De même, $4$ est l’antécédent de $12$ par la fonction linéaire $p$.
- Ne pas confondre $p(4)$ et $p\times (4)$.
- Pour calculer $f(x)$, on multiplie $x$ par $a$ le coefficient de la fonction linéaire.
Coefficient d’une fonction linéaire
Exemple : Soit $f$ une fonction linéaire tel que : $f(-5)=20$. Calculons $f(-7)$.
$f$ est une fonction linéaire, donc $f(x)=ax$.
Or : $f(-5)=20$, alors : $$a=\dfrac{f(-5)}{-5}=\dfrac{20}{-5}=-4.$$
Par conséquent : $$f(x)=-4x.$$
Donc : $$f(-7)=-4\times (-7)=28.$$
Représentation graphique d’une fonction linéaire
- La représentation graphique ou la courbe d’une fonction linéaire $f$ est notée $(C_f)$ ou $(D)$.
- $M(x;y)$ est un point de $\left(C_f\right)$ signifie que : $f(x)=y.$
Exemple : Représentation graphique de la fonction linéaire $f$ définie par : $f(x)=2x.$
On calcule :
$$f(1) = 2 \times 1 = 2$$
Ainsi, la représentation graphique de $f$ est la droite $(D)$ qui passe par l’origine $O(0;0)$ du repère et par le point $A(1;2)$.
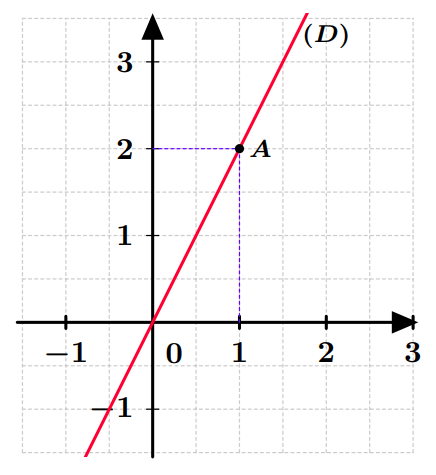
On a toujours : $$f(0) = 0 \quad \text{et} \quad f(1) = a$$





