Fonctions affines
La relation $f$ qui, à tout nombre réel $x$, associe le nombre $ax+b$, est appelée une fonction affine de coefficient $a$.
On la note :
$$f : x \mapsto ax+b$$
Le nombre $ax+b$ est l’image de $x$ par $f$, et on écrit : $f(x)=ax+b.$
Exemple : On considère la fonction définie par :
$$g(x)=-5x+3$$
- $g$ est une fonction affine de coefficient $-5$. $\,\,(a=-5 \text{ et } b=3)$.
- On a : $g(-2)=-5\times (-2)+3=10+3=13$. Donc, l’image de $-2$ par $g$ est $13.$
- On a : $g(7)=-5\times (7)+3=-35+3=-32$. Donc, l’antécédent de $-32$ par $g$ est $7.$
- Toute fonction linéaire est une fonction affine particulière de la forme :
$$f(x)=ax+0=f(x)=ax.$$ - Toute fonction constante est une fonction affine particulière de la forme :
$$f(x)=0\times x+b=f(x)=b.$$
Coefficient d’une fonction affines
Si $f$ est une fonction affine, alors $\dfrac{f(x_1)-f(x_2)}{x_1-x_1}$ est le coefficient de $f$.
Exemple : Soit $f$ une fonction affine tel que : $f(-2)=4$ et $f(5)=7$. Calculons $f(8)$.
On sait que :$$\frac{{f\left( 8 \right) -f\left( 5 \right)}}{{8 -5}} = \frac{{f\left( { -2} \right) -f\left( 5 \right)}}{{ -2 -5}}\,\,\,\left(\text{Coefficient de la fonction affine } f \right)$$Donc : \[\frac{{f\left( 8 \right) -7}}{3} = \frac{{4 -7}}{{ -7}}\]Donc : \[f\left( 8 \right) -7 = \frac{9}{7}\]Donc : \[f\left( 8 \right) = \frac{9}{7} + 7\]D’où : \[f\left( 8 \right) = \frac{{58}}{7}\]
Représentation graphique d’une fonction affine
- $M(x;y)$ est un point de $\left(C_f\right)$ signifie que : $f(x)=y.$
Exemple : Représentation graphique de la fonction affine $g$ définie par : $g(x)=3x-2.$
On calcule :
$$\begin{aligned}
g(0) &= 3 \times 0 -2 = -2\\
g(1) &= 3 \times 1 -2 = 1
\end{aligned}$$
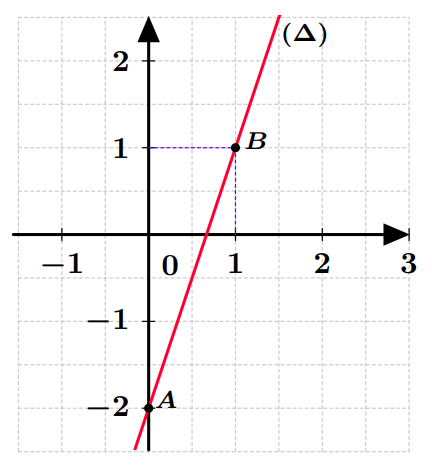
Ainsi, la représentation graphique de $g$ est la droite $(\Delta)$ qui passe par les points $A(0;-2)$ et $B(1;1)$.
- La représentation graphique d’une fonction constante est parallèle à l’axe des abscisses.
- La représentation graphique d’une fonction nulle est l’axe des abscisses.





