Équation réduite d’une droite
Définition : Soit $(O;I;J)$ un repère orthonormé.
Toute droite $(\Delta)$ non parallèle à l’axe des ordonnées admet une équation réduite de la forme : $y=mx+p$, où $m$ et $p$ deux nombre réels.
- Le nombre $m$ est le coefficient directeur.
- Le nombre $p$ est l’ordonnée à l’origine.
Exemple :
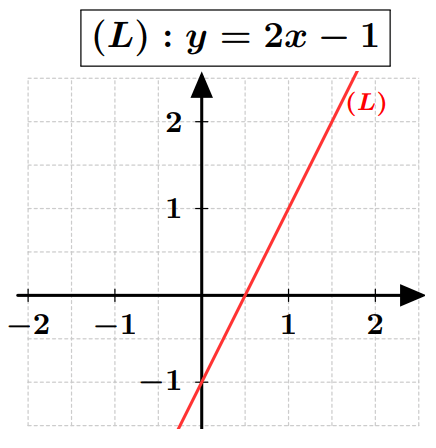
Cas particuliers :
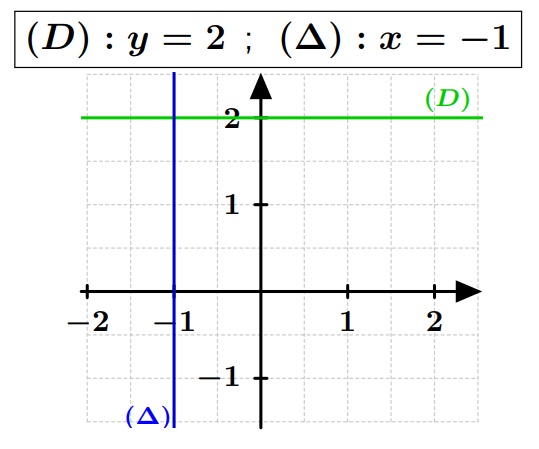
- Si l’équation est : $y=a$, alors la droite est parallèle à l’axe des abscisses.
- Si l’équation est : $x=b$, alors la droite est parallèle à l’axe des ordonnées.

Remarque : On considère la droite : $(\Delta) : y=mx+p$
- Si le point $M(x_M;y_M)$ appartient à la droite $(\Delta)$ signifie que : $y_M=mx_M+p$
Déterminer l’équation réduite d’une droite
Propriété : Si $A(x_A;y_A)$ et $A(x_B;y_B)$ deux points, avec $x_A\neq x_B$. Alors :
- Le coefficient directeur de la droite $(AB)$ est : $m=\dfrac{y_B-y_A}{x_B-x_A}$.
- L’ordonnée à l’origine est : $p=y_A-mx_A$
Exemple : On détermine l’équation de la droite $(AB)$ tels que : $A(7;3)$ et $B(-1;1)$.
- Le coefficient directeur est : $$m=\dfrac{y_B-y_A}{x_B-x_A}=\dfrac{1-3}{-1-7}=\dfrac{-2}{-8}=\dfrac{1}{4}$$
- L’ordonnée à l’origine est : $$p=y_A-mx_A=3-\dfrac{1}{4}\times 7=\dfrac{12}{4}-\dfrac{7}{4}=\dfrac{5}{4}$$
Donc l’équation réduite de la droite $(AB)$ est : $$ y=\dfrac{1}{4}x+\dfrac{5}{4}$$
Droites parallèles
Propriété : Soient $(D)$ et $(D’)$ deux droites d’équations :
$(D): y=mx+p$ et $(D’): y=m’x+p’$
- Si $(D)\parallel(D’)$, alors $m=m’$.
- Si $m=m’$, alors $(D)\parallel(D’)$.
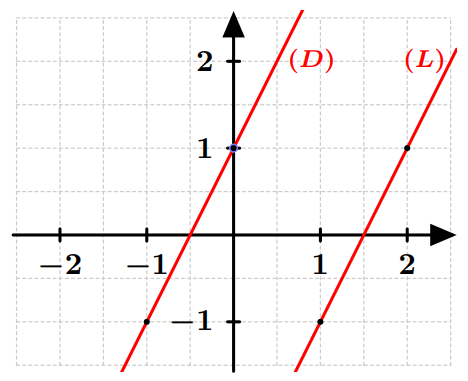
Exemple : Les deux droites $(D)$ et $(L)$ d’équations :
$(D): y=2x+1$ et $(L): y=2x-3$
ont le même coefficient directeur qui $2$, donc : $(D) \parallel (L)$.
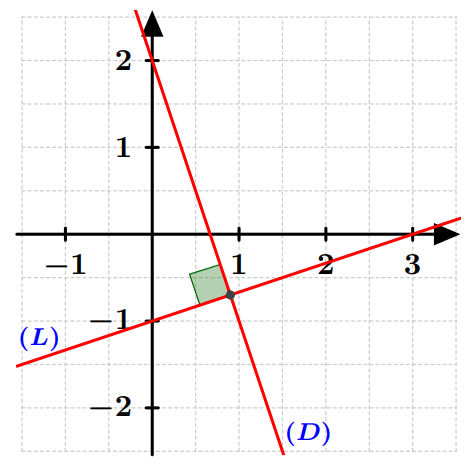
Droites perpendiculaires
Propriété : Soient $(D)$ et $(D’)$ deux droites d’équations :
$(D): y=mx+p$ et $(D’): y=m’x+p’$
- Si $(D)\perp(D’)$, alors $m\times m’=-1$.
- Si $m\times m’=-1$, alors $(D)\perp(D’)$.
Exemple : On considère les deux droites $(D)$ et $(L)$ d’équations :
$(D): y=-3x+2$ et $(L): y=\dfrac{1}{3}x-1$
On a : $-3\times \dfrac{1}{3}=-1$, donc $(D)\perp(L)$.