Chapitre 2

Notions d’ensembles

Un ensemble est une collection d’objets. Les objets qui forment l’ensemble sont appellés les éléments de cet ensemble.

Exemples : $A=\big\{-1;3;5\big\}$ et $B=\big\{a;b;c;d\big\}$ sont des ensembles. $-1$, $3$ et $5$ sont les élements de l’ensemble $A$ et on écrit $3\in A$ (lire $3$ appartient à $A$) et $8\not\in A$ (lire $8$ n’appartient pas à $A$)

Définition : (ensemble vide)
L’ensemble qui ne contient aucun élément est appelé l’ensemble vide et est noté $\varnothing$.

Définition : (sous ensemble)
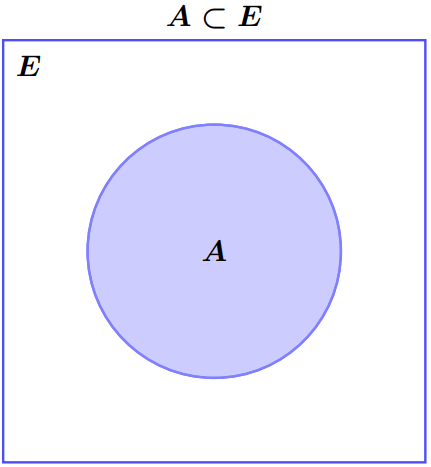
On dit qu’un ensemble $A$ est un sous ensemble ou une partie de $E$ si tout élément de $A$ est un élement de $E$, et on note $A\subset E$.

Exemlpe : $A=\{-3;9\}$ est une partie de $E=\{-5;-3;6;9;13\}$

Définition : (Égalité de deux ensemble)
Soit $E$ et $F$ deux ensembles.
On dit que $E$ et $F$ sont égaux lorsqu’ils ont les mêmes éléments et on écrit $E=F$.

Exemlpe : Si $A=\{x\in\mathbb{R}; |x|\le 2\}$ et $B=\big[-2;2\big]$, alors $A=B$

Inclusion

Définition : Soit $A$ et $B$ deux parties d’un ensemble $E$.
On dit que $A$ est incluse dans $B$ si tout élément de $A$ appartient à $B$, et on écrit $A \subset B$.\[\left[ {A \subset B} \right] \Leftrightarrow \left[ {\left( {\forall x \in E} \right);\,\,x \in A \Rightarrow x \in B} \right]\]On a toujours : $\varnothing \subset A$ et $A \subset A$.

Exemples :

On cosidère l’ensemble : $E=\{-5;-3;0;4;9\}$. On a : $$\{4\} \subset E\quad ; \quad\{-5;0;9\} \subset E\quad ; \quad\{-3;-1;4\}\not\subset E$$
On a : $$\mathbb{N}\subset\mathbb{Z}\subset\mathbb{Q}\subset\mathbb{R}\quad ; \quad\left] {0; + \infty } \right[ \subset \mathbb{R}\quad ; \quad\{0;3;7;8\}\subset \mathbb{N}$$

Proposition : Soit $A$, $B$ et $C$ trois parties d’un ensemble $E$.

$\bullet\quad A = B \Leftrightarrow \left( {A \subset B\,\,\,et\,\,B \subset A} \right)$

$\bullet\quad \left\{ \begin{array}{l}
A \subset B\\
B \subset C
\end{array} \right.\,\,\, \Rightarrow \,\,\,A \subset C$

Ensemble des parties d’un ensemble

Définition : Soit $E$ un ensemble.
L’ensemble des parties d’un ensemble $E$ est un ensemble dont les éléments sont les parties de $E$.
Cet ensemble dont les éléments sont les sous-ensembles de $E$ est noté $\mathscr{P}(E)$. $$A \subset E \Longleftrightarrow A \in \mathscr{P}(E).$$

Remarques :

$\varnothing \in E \quad$ (ici $\varnothing$ est un élément)
$\varnothing \subset \mathscr{P}(E)$ (ici $\varnothing$ est un ensemble)
Le nombre de parties d’un ensemble $E$ constitué de $n$ éléments est égal à $2^n$.

Exemples : On cosidère l’ensemble $E=\{x,y,z\}$, dans ce cas, $\mathscr{P}(E)$ est constitué des $2^3=8$ éléments suivants : $$\mathscr{P}(E)=\Big\{\{\varnothing\},\{x\},\{y\},\{z\},\{x,y\},\{x,z\},\{y,z\},\{x,y,z\}\Big\}$$

Complémentaire

Définition : Soit $A$ une partie d’un ensemble $E$.
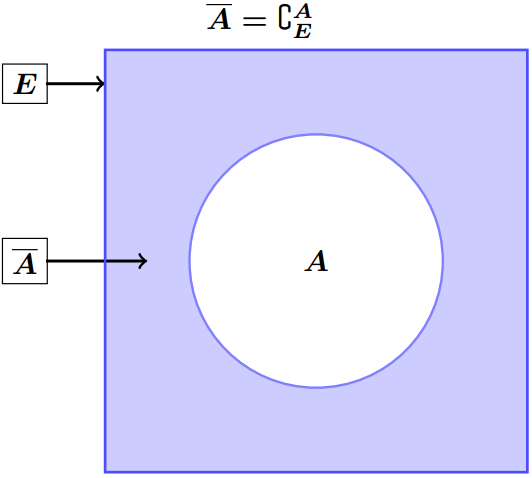
L’ensemble des éléments de $E$ n’appartenant pas à l’ensemble $A$ est appelé le complémentaire de $A$ dans $E$. on le note $\complement_E^A$ ou $\overline A$.
On a : $$\complement_E^A=\big\{x\in E/ x\not\in A\big\}\quad\text{et}\quad x\in \overline A \Leftrightarrow x\not\in A$$

Exemples :

On a : $\quad\complement_\mathbb{N}^{\{0\}}=\mathbb{N}^*\quad$ ; $\quad\complement_{\mathbb{R}}^{\mathbb{R}^*}=\{0\}\quad$ ; $\quad\complement_{\mathbb{R}}^{[0;2]}=\left] { – \infty ;0} \right[ \cup \left] {2; + \infty } \right[$
On cosidère les deux ensembles : $$E=\big\{e_1,e_2,e_3,e_4,e_5,e_6\big\}\quad \text{et}\quad A=\big\{e_1,e_2\big\}$$ Dans ce cas, on a : $$\complement_{E}^{A}=\big\{e_3,e_4,e_5,e_6\big\}$$

Proposition : Soit $A$ et $B$ deux parties d’un ensemble $E$. On a :

$\bullet\quad \overline \varnothing =E\quad$ et $\quad\overline E =\varnothing$

$\bullet\quad \overline{(\overline A)} =A$

$\bullet\quad A \subset B \Leftrightarrow \overline B \subset \overline A$

Intersection

Définition : Soit $A$ et $B$ deux parties d’un ensemble $E$.
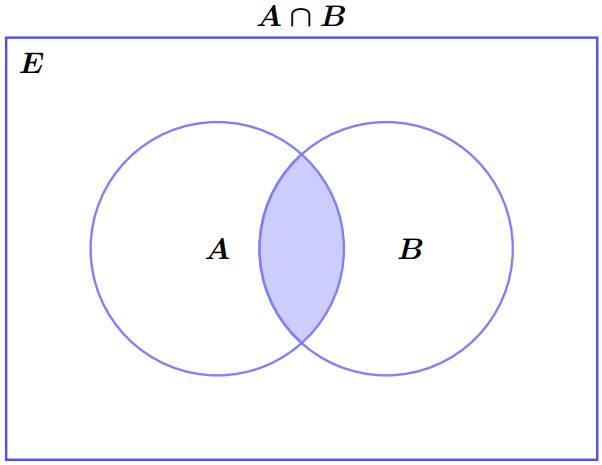
L’intersection des ensembles $A$ et $B$, ontée $A \cap B$, est l’ensemble des éléments de$E$ qui sont dans $A$ et dans $B$. C’est-à-dire :
\[x \in A \cap B \Leftrightarrow \left( {x \in A\,\,\text{ et }\,\,x \in B} \right)\] On a alors : \[A \cap B = \left\{ {x \in E/\,\,x \in A\,\,\text{ et }\,\,x \in B} \right\}\]

Exemples : On considères les ensemble suivantes : $$A=\big\{a,b,c,d\big\}\quad\text{et}\quad B=\big\{a,b,c,e\big\}$$ Dans ce cas, on a : $$A \cap B =\big\{a,b,c\big\}$$

Proposition : Soit $A$, $B$ et $C$ trois parties d’un ensemble $E$.
$$\begin{array}{ll}
\mathbf{1.}\ A \cap B=B \cap A &\quad\quad\mathbf{2.}\ A \cap E=A\\
\mathbf{3.}\ A \cap \varnothing=\varnothing &\quad\quad\mathbf{4.}\ A \cap A=A\\
\mathbf{5.}\ A \cap \bar{A}=\varnothing &\quad\quad\mathbf{6.}\ A \cap B \subset A\\
\mathbf{7.}\ A \cap B \subset B &\quad\quad\mathbf{8.}\ A \cap B=A \Leftrightarrow A \subset B\\
\mathbf{9.}\ A \cap (B \cap C)=(A\cap B)\cap C &\quad\quad\\
\end{array}$$

Réunion

Définition : Soit $A$ et $B$ deux parties d’un ensemble $E$.
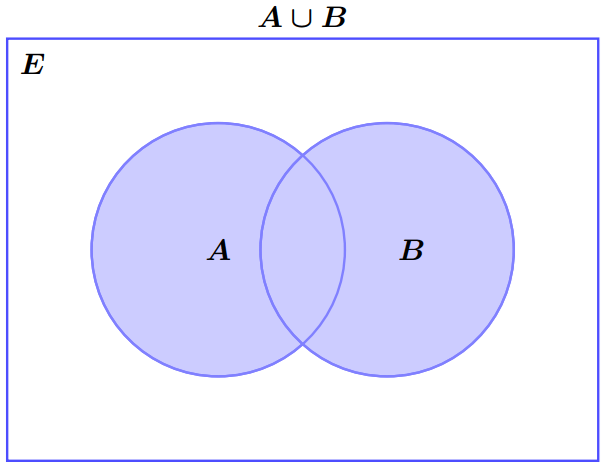
La réunion des ensembles $A$ et $B$, ontée $A \cup B$, est l’ensemble des éléments de $E$ qui sont dans $A$ ou dans $B$. C’est-à-dire :
\[x \in A \cup B \Leftrightarrow \left( {x \in A\,\,\text{ ou }\,\,x \in B} \right)\] On a alors : \[A \cup B = \left\{ {x \in E/\,\,x \in A\,\,\text{ ou }\,\,x \in B} \right\}\]

Exemples : On considères les ensemble suivantes : $$A=\big\{a,b,c,d\big\}\quad\text{et}\quad B=\big\{a,b,c,e\big\}$$ Dans ce cas, on a : $$A \cup B =\big\{a,b,c,d,e\big\}$$

Proposition : Soit $A$, $B$ et $C$ trois parties d’un ensemble $E$.
$$\begin{array}{ll}
\mathbf{1.}\ A \cup B=B \cup A &\quad\quad\mathbf{2.}\ A \cup E=E\\
\mathbf{3.}\ A \cup \varnothing=A &\quad\quad\mathbf{4.}\ A \cup A=A\\
\mathbf{5.}\ A \cup \bar{A}=E &\quad\quad\mathbf{6.}\ A \subset A \cup B\\
\mathbf{7.}\ B \subset A \cup B &\quad\quad\mathbf{8.}\ A \cup B=A \Leftrightarrow B\subset A\\
\mathbf{9.}\ A \cup (B \cup C)=(A\cup B)\cup C &\quad\quad
\end{array}$$

Proposition : Soit $A$, $B$ et $C$ trois parties d’un ensemble $E$. \[\begin{aligned}
&\bullet\quad A \cup \left( {B \cap C} \right) = \left( {A \cup B} \right) \cap \left( {A \cap C} \right)\\
&\bullet\quad A \cap \left( {B \cup C} \right) = \left( {A \cap B} \right) \cup \left( {A \cap C} \right)
\end{aligned}\]

Lois de Morgan : Soit $A$, $B$ et $C$ trois parties d’un ensemble $E$. \[\begin{aligned}
&\bullet\quad\overline {B \cap C} = \overline A \cup \overline B \\
&\bullet\quad\overline {B \cup C} = \overline A \cap \overline B
\end{aligned}\]

Différence de deux ensembles

Définition : Soit $A$ et $B$ deux parties d’un ensemble $E$.
La différence des ensembles $A$ et $B$, ontée $A\backslash B$, est l’ensemble des éléments de $A$ qui ne sont pas dans $B$. C’est-à-dire :
\[x \in A \backslash B \Leftrightarrow \left( {x \in A\,\,\text{ et }\,\,x \not\in B} \right)\] On a alors : \[A \backslash B = \left\{ {x \in E/\,\,x \in A\,\,\text{ et }\,\,x \not\in B} \right\}\]

Exemples : On considères les ensemble suivantes : $$A=\big\{a,b,c,d,e,f\big\}\quad\text{et}\quad B=\big\{e,f,g,h\big\}$$ Dans ce cas, on a : $$A \backslash B =\big\{a,b,c,d\big\}$$

Proposition : Soit $A$ et $B$ deux parties d’un ensemble $E$. \[\begin{aligned}
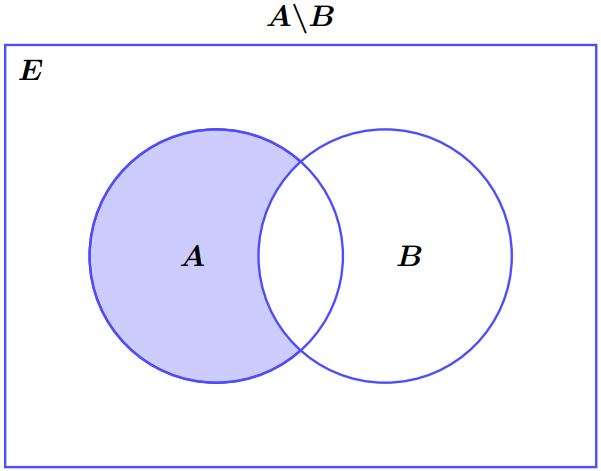
&\bullet\quad A\backslash B = A \cap \overline B \\
&\bullet\quad A = \left( {A\backslash B} \right) \cup \left( {A \cap B} \right)
\end{aligned}\]

Produit cartésien

Définition : Soit $E$ et $F$ deux ensembles.
Le produit cartésien des ensembles $E$ et $F$, ontée $E\times F$, est l’ensemble des couple $(x,y)$ tels que $x\in E$ et $y\in F$. C’est-à-dire :
\[(x,y) \in E\times F \Leftrightarrow \big( {x \in E\,\,\text{ et }\,\,y \in F} \big)\] On a alors : \[E\times F = \left\{ {(x,y) /\,\,x \in E\,\,\text{ et }\,\,y \in F} \right\}\]

Exemples : On considères les ensemble suivantes : $$E=\big\{a,b,c\big\}\quad\text{et}\quad F=\big\{x,y\big\}$$ Dans ce cas, on a : \[\begin{aligned}
&E \times F = \left\{ {\left( {a,x} \right),\left( {a,y} \right),\left( {b,x} \right),\left( {b,y} \right),\left( {c,x} \right),\left( {c,y} \right)} \right\}\\
&F \times E = \left\{ {\left( {x,a} \right),\left( {x,b} \right),\left( {x,c} \right),\left( {y,a} \right),\left( {y,b} \right),\left( {y,c} \right)} \right\}\\
&{E^2} = \left\{ {\left( {a,a} \right),\left( {a,b} \right),\left( {a,c} \right),\left( {b,a} \right),\left( {b,b} \right),\left( {b,c} \right),\left( {c,a} \right),\left( {c,b} \right),\left( {c,c} \right)} \right\}\\
&{F^2} = \left\{ {\left( {x,x} \right),\left( {x,y} \right),\left( {y,x} \right),\left( {y,y} \right)} \right\}
\end{aligned}\] À partir des exemples, il est clair que $E\times F \neq F\times E$.

La différence symétrique de deux ensembles

Définition : La différence symétrique de deux ensembles $A$ et $B$, notée $A\Delta B$, est l’ensemble des éléments qui appartiennent soit à $A$ soit à $B$, mais pas aux deux à la fois.
Autrement dit, elle représente les éléments qui sont dans l’un des ensembles mais pas dans leur intersection.

Formellement :$$A \Delta B = (A \setminus B) \cup (B \setminus A)$$

Cela peut également être exprimé de la manière suivante :

$$A \Delta B = (A \cup B) \setminus (A \cap B)$$

Exemple : Si $A = \{1, 2, 3\}$ et $B = \{3, 4, 5\}$, alors :$$A \Delta B = \{1, 2, 4, 5\}$$

Les éléments communs (ici $3$) sont exclus.