Chapitre 8
Angle au centre :
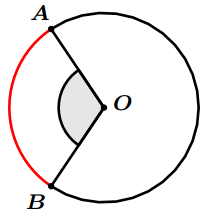
Définition 1 : Sur le dessin ci-contre où $O$ le centre du cercle $(C)$,
L’angle $\widehat{A O B}$ est appelé angle au centre qui intercepte l’arc $\overparen{A B}$.
L’angle $\widehat{A O B}$ est appelé angle au centre qui intercepte l’arc $\overparen{A B}$.
Angle inscrit
Définition 2 : Soit $(C)$ un cercle de centre $O$.
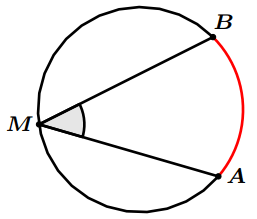
L’angle $\widehat{A M B}$ est appelé angle inscrit du cercle qui intercepte l’arc $\overparen{A B}$
- $A$, $B$ et $M$ trois points du cercle $(C)$.

L’angle $\widehat{A M B}$ est appelé angle inscrit du cercle qui intercepte l’arc $\overparen{A B}$
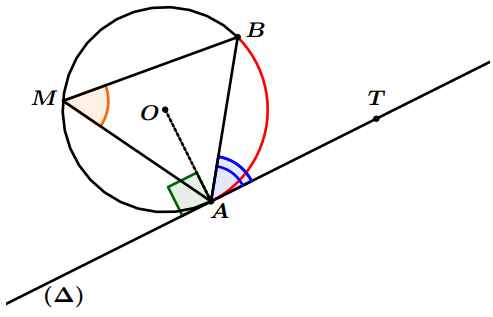
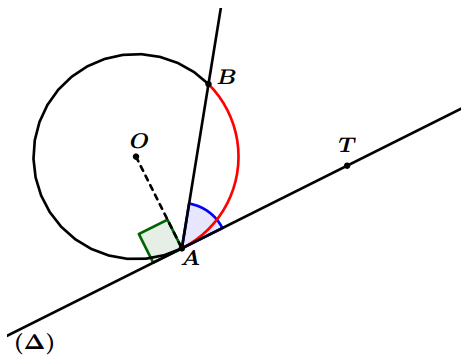
- Soit ( $\Delta$ ) la tangente du cercle $(C)$ au point $A$.

Angle inscrit et angle au centre associé
Propriété 1 : La mesure d’un angle inscrit dans un cercle est égale à la moitié de la mesure de l’angle au centre associé.
Exemple : Sur le dessin suivant :
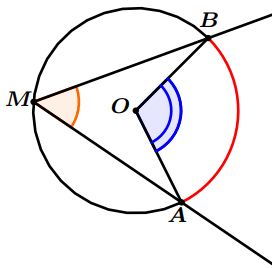
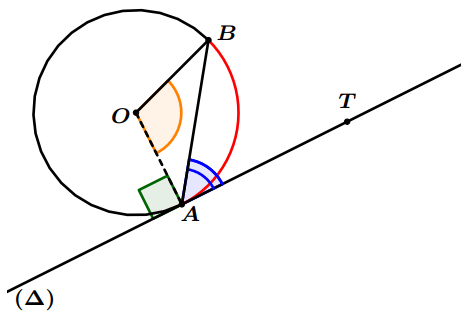
Propriété 2 : Soit $(\Delta)$ la tangente du cercle $(C)$ au point $A$ et $T$ un point de ($\Delta$), on a : $$\widehat{AOB}=2 \widehat{TAB}$$

Angles inscrits interceptant le même arc
Propriété 3 : Si deux angles inscrits dans un cercle interceptent le même arc, alors ces angles ont la même mesure.
Exemple : Sur le dessin suivant :
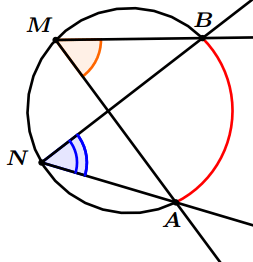
$\widehat{A M B}$ et $\widehat{A N B}$ sont deux angles inscrits qui interceptent le même arc donc : $\widehat{A M B}=\widehat{ANB}$.
Propriété 4 : Soit $(\Delta)$ la tangente du cercle $(C)$ au point $A$ et $T$ un point de $(\Delta)$, on a :$$\widehat{TAB}=\widehat{AMB}$$