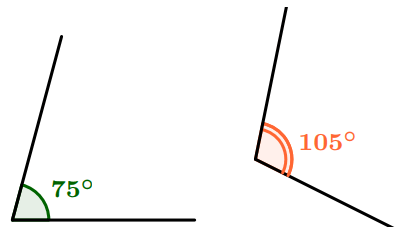
Angles
Définition : Un angle est une portion du plan délimité par deux demi-droites de même origine.
- L’origine de ses deux demi-droites est le sommet de l’angle.
- Ces deux demi-droites sont les côtés de l’angle.
Exemple :
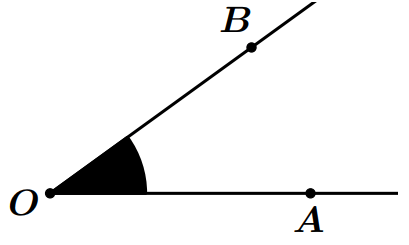
- L’angle noir est noté $\widehat {AOB}$.
- $O$ est le sommet de l’angle $\widehat {AOB}$.
- Les demi-droites $[OA)$ et $[OB)$ sont les cotés de l’angle $\widehat {AOB}$.
Remarques :
- Pour mesurer un angle on utilise le rapporteur.
- L’unité de mesure des angles est le degré.
Angles particuliers
Angle nul
- La mesure d’un angle nul est égale à $0^\circ$.
- Les cotes d’un angle nul sont confondues.

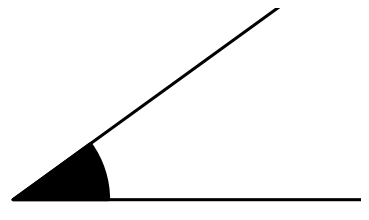
Angle aigu
La mesure de l’angle aigu est comprise entre $0^\circ$ et $90^\circ$.
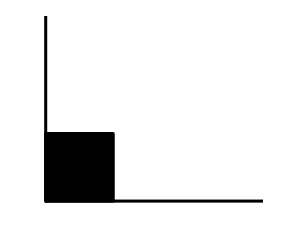
Angle droit
La mesure d’un angle droit est égale à $90^\circ$.
Angle obtus
La mesure de l’angle obtus est comprise entre $90^\circ$ et $180^\circ$.

Angle plat
La mesure d’un angle plat est égale à $180^\circ.$

Angle plein
La mesure d’un angle plein est égale à $360^\circ.$
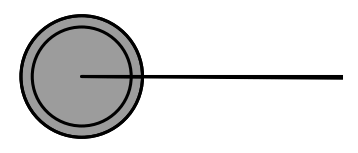
Relation entre deux angles
Angles adjacents
Définition : Deux angles adjacents sont deux angles qui :
- ont le même sommet;
- ont un côté commun;
- sont situés de part et d’autre de ce côté commun.
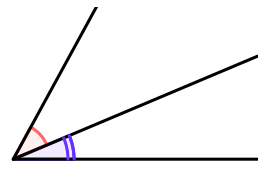
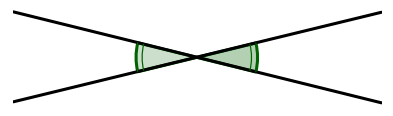
Angles opposés par le sommet
Définition :
- Deux angles opposés par le sommet sont deux angles qui ont le même sommet et leurs côtés sont dans le prolongement l’un de l’autre.
- Deux angles opposés par le sommet sont égaux.
Angles complémentaires
Définition : Deux angles sont complémentaires si la somme de leurs mesures est égale à $90^\circ$.
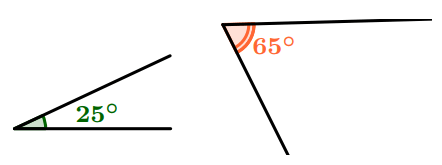
Angles supplémentaires
Définition : Deux angles sont supplémentaires si la somme de leurs mesures est égale à $180^\circ$.