Cours : Systèmes – 3ac

Système de deux équations à deux inconnues du premier degré

Définition 1 : Un système de deux équations à deux inconnues du premier degré est de la forme :
$$\left\{ \begin{array}{l}
ax + by = c\\
dx + ey = f
\end{array} \right.$$où $a$, $b$, $c$, $d$, $e$ et $f$ sont des nombres réels donnés.

$x$ et $y$ sont les inconnues.
Un couple $(x ; y)$ vérifiant les deux équations en même temps, est une solution du système.

Exemples :
$$\left\{ \begin{aligned}
& 2x -3y = 7\\
& x + 5y = -3
\end{aligned} \right. ~~;~~
\left\{ \begin{aligned}
& \sqrt 2 x + \dfrac{2}{3}y = 5\\
& -x + \sqrt 3 y = \dfrac{{ -1}}{2}
\end{aligned} \right.~~;~~
\left\{ \begin{aligned}
&\dfrac{{x + 2}}{3} + \dfrac{{y -4}}{2} = -6\\
&\dfrac{{4x + 1}}{5} + \dfrac{{3y}}{2} = -4
\end{aligned} \right.$$Ce sont des systèmes de deux équations à deux inconnues du premier degré.

Définition 2 : Résoudre un système, c’est trouver tous les couple $(x;y)$ qui vérifient à la fois les deux équations.

Exemple : Le couple $(5;9)$ est une solution du système : $$\left\{ \begin{aligned}
& 2x -y = 1\\
& -4x + 3y = 7
\end{aligned} \right.$$ Car :
$$\left\{ \begin{aligned}
& 2 \times 5 -9 = 10 -9 = 1\\
& -4 \times 5 + 3 \times 9 = -20 + 27 = 7
\end{aligned} \right.$$

Résolution algébrique d’un système

Méthode de substitution

Règle : Dans cette méthode, on exprime l’une des deux inconnues en fonction de l’autre à partir d’une équation, puis on remplace cette expression dans l’autre équation. On obtient ainsi une équation à une seule inconnue.

Exemple : Résoudre, par substitution, le système suivant :
$$
\begin{cases}
2x -3y = 7 & (1) \\
x + 5y = -3 & (2)
\end{cases}
$$

Dans l’équation $(2)$, on exprime $x$ en fonction de $y$ :

$$
\boxed{x = -3 -5y} \quad (3)
$$

On remplace $x$ par $-3 -5y$ dans l’équation $(1)$ :

$$
\begin{array}{c}
2(-3 -5y) -3y = 7 \\
-6 -10y -3y = 7 \\
-6 -13y = 7 \\
-13y = 13 \\
y = \frac{13}{-13} \\
y = -1
\end{array}
$$

On remplace $y = -1$ dans l’équation $(3)$ :

$$
\begin{aligned}
x &= -3 -5\times (-1) \\
x &= -3 + 5 \\
x &= 2
\end{aligned}
$$

Donc la solution du système est le couple :

$$
\boxed{(2 \, ; \, -1)}
$$

Méthode de combinaison linéaire

Règle : Dans cette méthode, on multiplie les deux équations par des coefficients convenablement choisis, puis on les additionne (membre à membre) de façon à éliminer l’une des deux inconnues.

Exemple : Résoudre, par combinaison linéaire, le système :

$$
\begin{cases}
3x -4y = 32 & (1) \\
7x -6y = 58 & (2)
\end{cases}
$$

Pour éliminer $y$, on multiplie l’équation $(1)$ par $-3$ et l’équation $(2)$ par $2$. On obtient :

$$
\begin{cases}
-9x + 12y = -96 & (3) \\
14x -12y = 116 & (4)
\end{cases}
$$

On additionne les équations $(3)$ et $(4)$ membre à membre :

$$
-9x + 12y + 14x -12y = -96 + 116 \\
5x = 20 \\
x = \frac{20}{5} \\
\boxed{x = 4}
$$

Pour éliminer $x$, on multiplie l’équation $(1)$ par $7$ et l’équation $(2)$ par $-3$. On obtient :

$$
\begin{cases}
21x -28y = 224 & (5) \\
-21x + 18y = -174 & (6)
\end{cases}
$$

On additionne les équations $(5)$ et $(6)$ membre à membre :

$$
21x -28y -21x + 18y = 224 -174 \\
-10y = 50 \\
y = \frac{50}{-10} \\
\boxed{y = -5}
$$

Donc la solution du système est le couple :
$$
\boxed{(4 \, ; \, -5)}
$$

Résolution graphique d’un système

Principe : À chaque équation du système, on associe la droite représentative correspondante. Résoudre graphiquement le système revient alors à déterminer, s’il existe, le point d’intersection de ces deux droites. Les coordonnées de ce point donnent la solution du système.

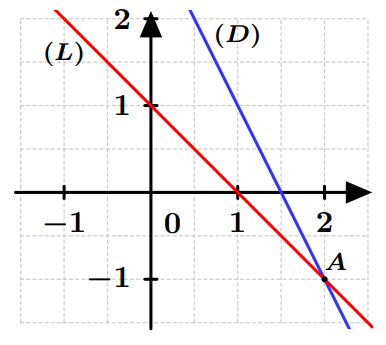
Exemple 1 : Résoudre graphiquement le système :
$$
\begin{cases}
2x + y = 3 \\
x + y = 1
\end{cases}
$$

On considère les droites associées :
$$
\begin{cases}
(D):~ y = -2x + 3 \\
(L):~ y = -x + 1
\end{cases}
$$

Les droites $(D)$ et $(L)$ n’ont pas le même coefficient directeur. Donc, elles sont sécantes.

Soit $A$ le point d’intersection de $(D)$ et $(L)$.

Par lecture graphique, on constate que les droites $(D)$ et $(L)$ se coupent en $A(2;−1)$. Ainsi, le couple $(2;−1)$ est solution du système.

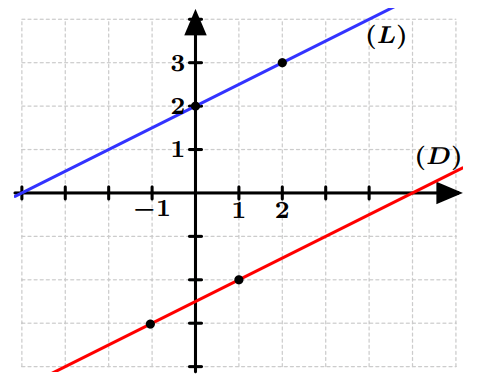
Exemple 2 : Résoudre graphiquement le système :
$$
\begin{cases}
x -2y = 5 \\
-2x + 4y = 8
\end{cases}
$$

On considère les droites associées :
$$
\begin{cases}
(D):~ y = \dfrac{1}{2}x -\tfrac{5}{2} \\
(L):~ y = \dfrac{1}{2}x + 2
\end{cases}
$$

Les droites $(D)$ et $(L)$ ont le même coefficient directeur mais des ordonnées à l’origine différentes. Donc, elles sont strictement parallèles.

Donc, le système n’a pas de solution.

Résolution de problèmes

Exemple : Yassine dispose de $13$ billets de $20$ dirhams et de $50$ dirhams.
Si la valeur totale de ces billets est de $500$ dirhams, déterminer le nombre de billets de chaque espèce.

Réponse :

Choix des inconnues :Soit $x$ le nombre de billets de $20$ DH.
Soit $y$ le nombre de billets de $50$ DH.
Mise en système :Le nombre total de billets est $13$, donc :
$$x + y = 13 \quad (1)$$

La valeur totale des billets est $500$ DH, donc :
$$20x + 50y = 500 \quad (2)$$

Donc le système est : $$\begin{cases}
x + y = 13 & {(1)} \\
20x + 50y = 500& {(2)}
\end{cases} $$
Résolution :D’après $(1)$ :
$$y = 13 -x \quad (3)$$

On remplace $y$ dans $(2)$ :
\[
\begin{array}{c}
20x + 50(13 -x) = 500 \\
20x + 650 -50x = 500 \\
-30x + 650 = 500 \\
-30x = -150 \\
x = \frac{-150}{-30} \\
\boxed{x = 5}
\end{array}
\]

On remplace $x = 5$ dans $(3)$ :
$$y = 13 -5 = \boxed{8}$$
Vérification :
$$
\begin{cases}
5 + 8 = 13 \\
20 \times 5 + 50 \times 8 = 100 + 400 = 500
\end{cases}
$$
Conclusion :
Yassine possède 5 billets de 20 DH et 8 billets de 50 DH.