ⓘ
Devoir Libre n°2
Premier Semestre
Niveau : 3èm année collège
Leçons ciblées : Théorème de Thalèse, ordre et opérations.
Enoncé 
Dans la figure suivante,
$AEF$ un triangle tels que :
- $AE=5cm$ et $AF=6cm$ et $EF=7cm$
- $M$ un point de $\left[ {AE} \right]$ tel que $AM = 2cm$
- $C$ un point de $\left[ {AF} \right]$ tel que $\left( {MC} \right)\parallel \left( {EF} \right)$
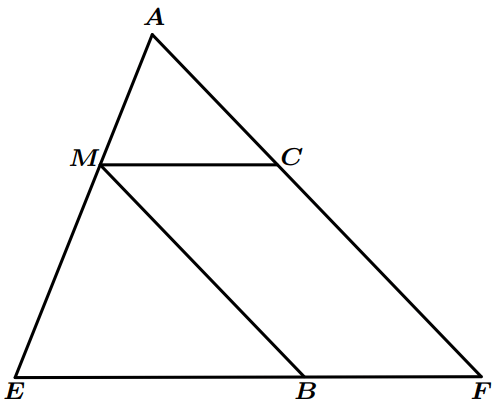
- Calculer $MC$
- Soit $B$ un point de $\left[ {EF} \right]$ tel que : $EB=4,2cm$.
Calculer $EM$
- Montrer que : $\left( {MB} \right)\parallel \left( {AF} \right)$
Indication 
- Appliquer le théorème de Thalès sur le triangle $AEF$.
Identifier les points $M \in [AE]$ et $C \in [AF]$, et utiliser que $(MC) \parallel (EF)$ pour établir le rapport.
- Utiliser que $M \in [AE]$, donc $EM = AE -AM$.
- Vérifier les rapports $\dfrac{EM}{EA}$ et $\dfrac{EB}{EF}$, puis appliquer la réciproque du théorème de Thalès sur le triangle $EAF$.
Corrigé 
- Dans le triangle $AEF$, on a :
$$M\in (AE), C\in (AF) \text{ et } (MC)\parallel(EF)$$ D’après le théorème de Thalès : $$\dfrac{AM}{AE}=\dfrac{AC}{AF}=\dfrac{MC}{EF}$$ On en déduit :$$\dfrac{AM}{AE}=\dfrac{MC}{EF}$$ En remplaçant : $$\dfrac{2}{5}=\dfrac{MC}{7}$$ Alors : $$MC=\dfrac{2\times 7}{5}=\dfrac{14}{5}=2,8.$$ Donc : $$\boxed{MC=2,8cm}$$
- Puisque $M\in[AE]$, alors : $$EM=AE-AM=5-2=3$$ Donc : $$\boxed{EM=3cm}$$
- Dans le triangle $EAF$, on a : $M\in(EA)$ et $B\in(EF)$.Les points $E,M,A$ ainsi que $E,B,F$ sont dans le même ordre.On compare les deux rapports : $$\dfrac{EM}{EA} \quad\text{ et }\quad \dfrac{EB}{EF}$$ On a : $$\dfrac{EM}{EA}=\dfrac{3}{5}\quad\text{et}\quad\dfrac{EB}{EF}=\dfrac{4,2}{7}=\dfrac{42}{70}=\dfrac{3\times 14}{5\times 14}=\dfrac{3}{5}$$ Ainsi : $$\dfrac{EM}{EA}=\dfrac{EB}{FE}.$$ D’après la réciproque du théorème de Thalès, on conclut que : $$\boxed{(MB)\parallel(AC)}$$
Enoncé 
On pose : $a = \sqrt {45} + 2\sqrt 5 $ et $b = 3\sqrt {20} $.
- Montrer que : $a -b = -\sqrt 5 $
- Déduire la comparaison de $a$ et $b$
Indication 
- Écris chaque radical sous forme $\sqrt{a^2 \times b}$ afin d’extraire le carré parfait. Regroupe ensuite les termes en $\sqrt{5}$ pour simplifier.
- Utilise le signe de $a -b$ pour comparer $a$ et $b$ : si $a−b < 0$, alors $a < b$.
Corrigé 
On pose : $a = \sqrt {45} + 2\sqrt 5 $ et $b = 3\sqrt {20} $
- On a : $$\begin{aligned}
a -b &=\sqrt {45} + 2\sqrt 5 -3\sqrt {20}\\
&=\sqrt{3^2\times 5} + 2\sqrt{5}-3\sqrt{2^2\times 5}\\
&=3\sqrt{5}+2\sqrt{5}-6\sqrt{5}\\
&=\boxed{- \sqrt 5} \end{aligned}$$
- Puisque $a-b=-\sqrt{5} < 0 $, alors $\boxed{a < b}$
Enoncé 
- Comparer les nombres suivants :
\begin{array}{lcl}
\mathbf a.\ 5\sqrt{2}~~\text{et}~~3\sqrt{5} &\quad\quad& \mathbf b.\ -\sqrt{30}~~\text{et} ~~-2\sqrt{7}
\end{array}
- Déduire la comparaison des nombres suivants :
\begin{array}{lcl}
\mathbf a.\ \dfrac{1}{{2 + 3\sqrt 5 }}~~\text{et}~~\dfrac{1}{{2 + 5\sqrt 2 }} &\quad\quad& \mathbf b.\ \sqrt {3 + \sqrt {30} } ~~\text{et} ~~\sqrt {3 + 2\sqrt 7 }
\end{array}
- Comparer les nombres : $\sqrt{2025}+1$ et $\sqrt{2026}$
Indication 
- Comparer d’abord les carrés des nombres, puis en déduire la comparaison des nombres eux-mêmes.
- Utiliser les résultats de la comparaison précédente, puis en déduire l’ordre des nouvelles expressions.
- Comparer d’abord les carrés des expressions, puis en déduire la comparaison des nombres.
Corrigé 
-
- Comparons $5\sqrt{2}$ et $3\sqrt{5}$On compare d’abord les carrés :$$
(5\sqrt{2})^2 -(3\sqrt{5})^2 = 25\times 2 -9\times 5 = 50 -45 = 5 > 0$$ alors : $$(5\sqrt{2})^2 > (3\sqrt{5})^2$$ Comme $5\sqrt{2}$ et $3\sqrt{5}$ sont positifs, alors :
$$\boxed{\,5\sqrt{2} > 3\sqrt{5}\,}$$
- Comparons $-\sqrt{30}$ et $-2\sqrt{7}$
$$
(-\sqrt{30})^2 -(-2\sqrt{7})^2 = 30 -4\times 7 = 30 -28 = 2 > 0$$ alors :
$$(-\sqrt{30})^2 > (-2\sqrt{7})^2$$
Les deux nombres étant négatifs, l’ordre s’inverse :
$$\boxed{\, -\sqrt{30} < -2\sqrt{7} \,}$$
- De $5\sqrt{2} > 3\sqrt{5}$ on obtient :
$$
2 + 5\sqrt{2} > 2 + 3\sqrt{5}$$ alors :
$$
\boxed{\,\dfrac{1}{2 + 5\sqrt{2}} < \dfrac{1}{2 + 3\sqrt{5}}\,}.
$$
- De $-\sqrt{30} < -2\sqrt{7}$ on déduit $$\sqrt{30} > 2\sqrt{7}$$ donc :
$$
3 + \sqrt{30} > 3 + 2\sqrt{7}$$
donc :
$$\boxed{\,\sqrt{\,3 + \sqrt{30}\,} > \sqrt{\,3 + 2\sqrt{7}\,}\,}.
$$
- Comparons : $\sqrt{2025} + 1$ et $\sqrt{2026}$.On compare les carrés : $$\begin{aligned}
(\sqrt{2025} + 1)^2 -(\sqrt{2026})^2 &= (2025 + 2\sqrt{2025} + 1) -2026\\
&= 2\sqrt{2025} > 0.\end{aligned}
$$
Donc : $(\sqrt{2025} + 1)^2 > (\sqrt{2026})^2$, d’où :
$$\boxed{\,\sqrt{2025} + 1 > \sqrt{2026}\,}$$
Enoncé 
Soient $a$, $b$ et $c$ trois nombres réels tels que :
$1 \le a \le 2~~;~~-3 \le b \le -2~~;~~1 \le \dfrac{1-2c}{3} \le \dfrac{5}{3}$
- Encadrer : $a+b$, $a-b$, $ab+6$ et $b^2-4$
- Montrer que : $ -2 \le c \le -1$
Indication 
- $\bullet$ Pour $a+b$ : Ajouter membre à membre les deux encadrements de même sens.$\bullet$ Pour $a-b$ : Commencer par encadrer de $-b$, puis utiliser $a+(-b)$.
$\bullet$ Pour $ab+6$ : D’abord encadrer $-b$ (positif), puis calculer $a\times(-b)$, en déduire $-ab$, puis $ab$, enfin ajouter $6$.
$\bullet$ Pour $b^2-4$ : Encadrer $b^2$ (négatif), ensuite soustraire $4$.
- Multiplier par $3$ (positif), soustraire $1$, diviser par $-2$ (attention, il faut changer le sens des inégalités).
Corrigé 
- $\bullet$ On a : $1 \le a \le 2$ et $-3 \le b \le -2$, alors : $$1+(-3) \le a+b \le 2+(-2),$$ donc $$\boxed{-2 \le a+b \le 0}$$ $\bullet$ On a : $1 \le a \le 2$ et $2 \le -b \le 3$, alors : $$1+2 \le a+(-b) \le 2+3,$$ donc : $$\boxed{3 \le a-b \le 5}$$ $\bullet$ On a : $1 \le a \le 2$ et $2 \le -b \le 3$, alors : $$1\times 2 \le a\times(-b) \le 2\times 3,$$ donc : $$2 \le -ab \le 6,$$ alors $$-6 \le ab \le -2,$$ alors : $$-6+6 \le ab+6 \le -2+6,$$ d’où : $$\boxed{0 \le ab+6 \le 4}$$ $\bullet$ On a : $-3 \le b \le -2$ alors : $$(-2)^2 \le b^2 \le (-3)^2,$$ donc : $$4 \le b^2 \le 9, $$ alors :$$4-4 \le b^2-4 \le 9-4$$ d’où : $$\boxed{0 \le b^2-4 \le 5}$$
- On a : $1 \le \dfrac{{1 – 2c}}{3} \le \dfrac{5}{3}$, alors : $$1 \times 3 \le \dfrac{{1 – 2c}}{3} \times 3 \le \dfrac{5}{3} \times 3,$$ alors : $$3 \le 1 – 2c \le 5,$$ alors : $$3 – 1 \le 1 – 2c – 1 \le 5 – 1,$$ alors : $$2 \le – 2c \le 4,$$ alors : $$\dfrac{2}{{ – 2}} \ge \dfrac{{ – 2c}}{{ – 2}} \ge \dfrac{4}{{ – 2}},$$ d’où : $$\boxed{ – 1 \ge c \ge – 2}$$
Enoncé 
Calculer et simplifier :
- $A = \sqrt {{{\left( {1 -\sqrt 2 } \right)}^2}} $
- $B = \sqrt {28 +10\sqrt 3 } $
- $C = 2\sqrt {28} + 3\sqrt {63} -13\sqrt 7 $
Indication 
- Pour $A$ : utilise $\sqrt {{X^2}} = \left\{ {\begin{array}{*{20}{c}}
X&{si\,\,\,\,X \ge 0}\\
{ – X}&{si\,\,\,\,X < 0}
\end{array}} \right.$ puis compare $1$ et $\sqrt{2}$.
- Pour $B$ : cherche à écrire $28+10\sqrt{3}$ sous la forme $(u+v\sqrt{3})^2$.
- Pour $C$ : mets $28$ et $63$ sous forme de carrés parfaits puis simplifie en $\sqrt{7}$.
Corrigé 
- On a : $2>1$, alors $\sqrt{2}>1$, donc $1-\sqrt{2}<0$, d'où : $$A = \sqrt {{{\left( {1 - \sqrt 2 } \right)}^2}} =-\left( {1 - \sqrt 2 } \right)=\boxed{\sqrt{2}-1}$$
- On remarque que : $28+10\sqrt 3=(5+\sqrt 3)^2$, donc : $$B = \sqrt {28 + 10\sqrt 3 } = \sqrt {{{\left( {5 + \sqrt 3 } \right)}^2}} = \boxed{5 + \sqrt 3 }$$ (car $5+\sqrt{3}>0$).
- On remarque que : $28=2^2\times 7$ et $63=3^2\times 7$, alors :
$$\begin{aligned}
C &= 2\sqrt {28} + 3\sqrt {63} -13\sqrt 7 \\
&= 2\sqrt {{2^2} \times 7} + 3\sqrt {{3^2} \times 7} -13\sqrt 7\\
&= 4\sqrt 7 + 9\sqrt 7 -13\sqrt 7\\
&= \left( {4 + 9 -13} \right)\sqrt 7 \\
&= \boxed{0}\end{aligned}$$
















