Chapitre 6

Théorème de Pythagore

Théorème 1 : Si un triangle est rectangle, alors le carré de l’hypoténuse est égal à la somme des carrés des cotées de l’angle droit.

Autrement dit : Si

$ABC$ un triangle rectangle en

$A$ , alors :

$AB^2+AC^2=BC^2.$

Exemple :

Résultat : Si

$ABC$ un triangle rectangle en

$A$ , alors :

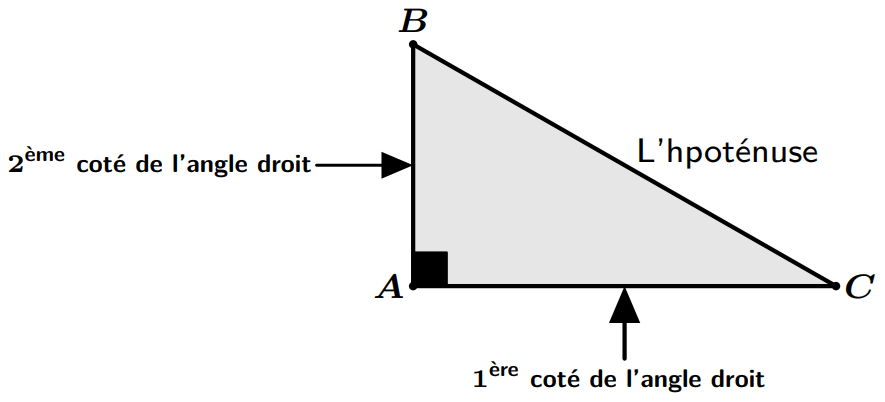
$AB^2=BC^2-AC^2\quad et \quad AC^2=BC^2-AB^2.$

Remarque : Le théorème de Pythagore sert à calculer des longueurs.

Application : $EFG$ triangle rectangle en $E$ tel que :
$EG = 2\sqrt{5}cm\quad ;\quad FG=6cm$

Calculer

$EF$ .

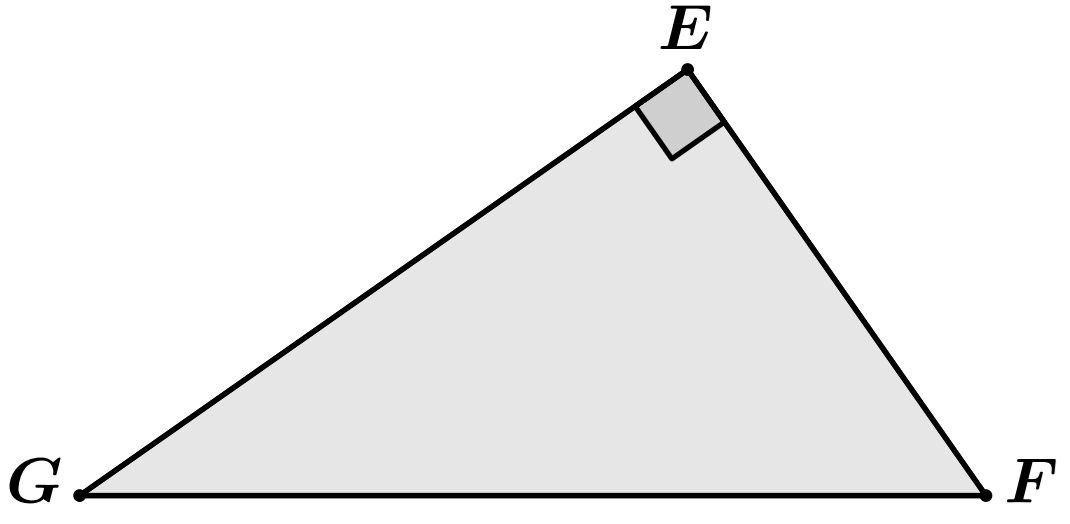
Réponse : Le triangle $EFG$ est rectangle en $E$ .

Donc d’après le théorème de Pythagore on a :
$E{F^2} + E{G^2} = F{G^2}$
Alors :
$\begin{aligned} E{F^2} &= F{G^2} – E{G^2}\\ &= {6^2} – {\left( {2\sqrt 5 } \right)^2}\\ &= 36 – 4 \times 5\\ &= 36 – 20\\ &= 16 \end{aligned}$
Puisque la distance est toujours positif, alors $\boxed{EF=\sqrt{16}cm=4cm}$

Réciproque du théorème de Pythagore

Théorème 2 : Si

$ABC$ un triangle tel que

$AB^2+AC^2=BC^2$ , alors

$ABC$ est un triangle rectangle en

$A$ .

Remarque : La réciproque du théorème de Pythagore sert à démontrer que deux droites sont perpendiculaires.

Application : Soit $ABC$ un triangle tel que :
$AB=\sqrt{7}cm ~~;~~ AC = 2cm~~;~~BC=\sqrt{3}cm$

Montrer que le triangle

$ABC$ est rectangle et préciser en quel sommet.

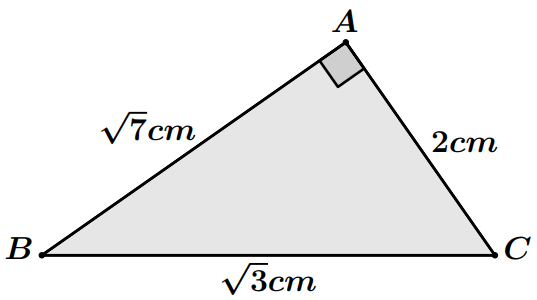
Réponse : On a : $AB^2=\sqrt{7}^2=7$ ; $AC^2=2^2=4$ et $BC^2=\sqrt{3}^2=3$

On remarque que : $4+3=7$

Ça veut dire que : $AC^2+BC^2=AB^2$

D’après la réciproque du théorème de Pythagore, le triangle $ABC$ est rectangle en $C$ .