Chapitre 5
Comparaison de deux nombres réels
Exemple : Comparons les nombres : $3 \sqrt{2}-5$ et $\sqrt{2}-7$.
On a : $\quad(\sqrt{2}-7)-(3 \sqrt{2}-5)=\sqrt{2}-7-3 \sqrt{2}+5=-2-2 \sqrt{2}$
Or : $\quad-2-2 \sqrt{2}$ est un nombre négatif,
alors : $(\sqrt{2}-7)-(3 \sqrt{2}-5)<0$
Donc : $\sqrt{2}-7<3 \sqrt{2}-5$.
Ordre et addition
Exemples :
- Si $x<8$, alors $x+2<8+2$, soit $x+2<10$.
- Si $x+9<2$, alors $x+9-9<2-9$, soit $x<-7$.
Ordre et multiplication
- Si $(a\leq b$ et $k>0)$, alors $ka \leq kb$.
- Si $(a \leq b$ et $k<0)$, alors $ka \geq kb$.
- $a$, $b$, $x$, $y$ sont des nombres réels positifs.
Si $a \leq x$ et $b \leq y$, alors: $ab \leq x y$.
Exemples :
- Si $x \leq-3$, alors $4 \times x \leq 4 \times(-3)$, soit $4 x \leq-12$.
- Si $\dfrac{-7}{6} x>\dfrac{12}{5}$, alors $\dfrac{-6}{7} \times \dfrac{-7}{6} x<\dfrac{-6}{7} \times \dfrac{12}{5}$, soit $x<-\dfrac{72}{35}$.
Ordre et inverse
$a \leq b$ signifie que : $\dfrac{1}{b} \leq \dfrac{1}{a}$.
Exemple : Si $\dfrac{1}{x^2}<\dfrac{2}{3}$, alors $x^2>\dfrac{3}{2}$.
Ordre et carré
- $a \leq b$ signifie que $a^2 \leq b^2$.
- $a \leq b$ signifie que $\sqrt{a} \leq \sqrt{b}$.
Exemple : Comparons les nombres positifs $5 \sqrt{2}$ et $4 \sqrt{3}$
On a : $(5 \sqrt{2})^2=50$ et $(4 \sqrt{3})^2=48$.
Donc: $(4 \sqrt{3})^2<(5 \sqrt{2})^2$.
D’où : $4 \sqrt{3}<5 \sqrt{2}$.
Racine carrée du carré d’un réel
- Si $x \geq 0$ alors $\sqrt{x^2}=x$.
- Si $x \leq 0$, alors $\sqrt{x^2}=-x$.
Exemple : $\sqrt{(\sqrt{3}-2)^2}=-(\sqrt{3}-2)=-\sqrt{3}+2$ car $\sqrt{3}<2$.
Chapitre 4
Théorème de Thalès
$B$ et $M$ deux points de la droite $(d_1)$, distincts de $A$.
$C$ et $N$ deux points de la droite $(d_2)$, distincts de $A$.
Si les droites $(BC)$ et $(MN)$ sont parallèles alors : $$\dfrac{AM}{AB}=\dfrac{AN}{AC}=\dfrac{MN}{BC}$$
Il y a trois configurations correspondantes à ce théorème.
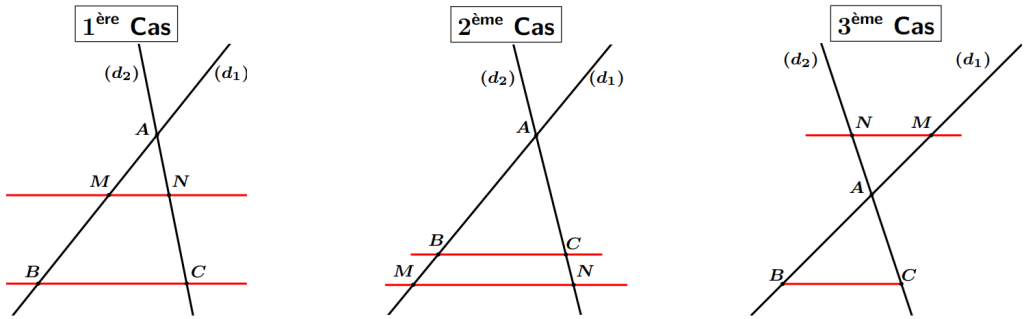
- Les points $A$, $B$, $M$ et $A$, $C$, $N$ sont alignés dans le même ordre.
- Le théorème de Thalès permet de calculer les longueurs.
Réciproque du théorème de Thalès
$B$ et $M$ deux points de la droite $(d_1)$, distincts de $A$.
$C$ et $N$ deux points de la droite $(d_2)$, distincts de $A$.
Si les $A$, $B$, $M$ et $A$, $C$, $N$ sont alignés dans le même ordre et $\dfrac{AM}{AB}=\dfrac{AN}{AC}$, alors les droites $(MN)$ et $(BC)$ sont parallèles.
Il y a deux configurations correspondantes à ce théorème.

- L’hypothèse « alignés dans le même ordre » est essentielle.
- La réciproque du théorème de Thalès permet de démontrer le parallélisme de deux droites.
Exemple : On considère la figure suivante:
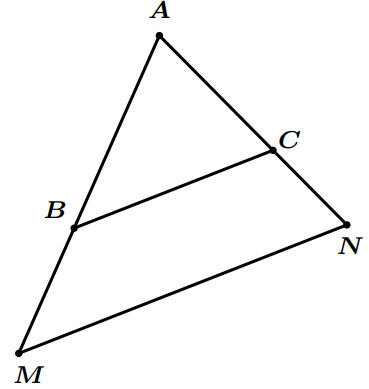
On donne : $AB=35cm$; $AM=40cm$; $AC=21cm$ ; $AN=24cm$
On a : $\dfrac{AM}{AB}=\dfrac{40}{35}=\dfrac{8}{7}$ et $\dfrac{AN}{AC}=\dfrac{24}{21}=\dfrac{8}{7}$, alors : $\dfrac{AM}{AB}=\dfrac{AN}{AC}$.
Et on sait que les points $A$, $B$, $M$ et $A$, $C$, $N$ sont alignés dans le même ordre.
Alors on peut conclure que les droites (BC) et $(MN)$ sont parallèles.

Calculer les nombres rationnels suivants :
$$A=\dfrac{3}{20}-\dfrac{11}{28} \quad;\quad B=\dfrac{7}{6}+\dfrac{-4}{9}$$

Calculer le nombre rationnel suivant : \[C = \frac{7}{{15}} – \frac{4}{3} + \frac{1}{5} – \frac{1}{3} – \frac{2}{{15}}\]

Calculer, de la manière la plus simple, l’expression suivant: \[E = -\frac{2}{3} + \left({- 1 + \frac{4}{3} – \frac{5}{2}} \right)- \left[ {1- \left( {\frac{1}{2} + \frac{7}{3}} \right)} \right]\]

$a$ et $b$ sont deux nombres rationnels tels que : $$-4a+2b=\dfrac{11}{6}$$
Calculer : $$F=-2a-\left(-b-1\right)+\left(-2a+b+2\right)-\left(-\dfrac{5}{6}\right)$$

Soit $x$ un entier positif non nul.
- Montrer que : $$\dfrac{1}{x}-\dfrac{1}{x+1}=\dfrac{1}{x(x+1)}.$$
- En déduire le résultat de la somme $S$ : $$S=\dfrac{1}{1\times 2}+\dfrac{1}{2\times 3}+\cdots+\dfrac{1}{998\times 999}+\dfrac{1}{999\times 1000}$$

$a$ et $b$ sont deux nombres rationnels tels que :
\[\begin{aligned}
a &= \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \cdots + \frac{1}{{2017}} + \frac{1}{{2018}}\\
b &= \frac{3}{2} + \frac{4}{3} + \frac{5}{4} + \frac{6}{5} + \cdots + \frac{{2018}}{{2017}} + \frac{{2019}}{{2018}}
\end{aligned}\]
Montrer que : $b-a=2017$

Calculer le nombre rationnel : $A=\dfrac{39}{-48}\times\dfrac{-64}{-26}$

Calculer le nombre rationnel : $B = \dfrac{9}{{ – 5}} \times \dfrac{{ – 20}}{3} \times \dfrac{{ – 18}}{{ – 14}}$

Calculer le nombre rationnel : $C=\dfrac{-12}{35}\div\dfrac{-21}{-20}$

Calculer le nombre rationnel $x$ tel que : $\dfrac{-3}{4}x=\dfrac{5}{32}$

$x$ est un nombre rationnel.
Développer et réduire les expressions suivantes : \[\begin{aligned}
A &= \frac{1}{3}x – \frac{4}{{15}} – \left( {\frac{5}{6}x – \frac{3}{2}} \right)\\
B &= \frac{2}{3}\left( {\frac{9}{4}x – 2} \right)
\end{aligned}\]

Badr dépense les $\dfrac{3}{8}$ de son argent de poche pour acheter des livres et $\dfrac{5}{12}$ de son argent de poche pour l’achat d’un jeu vidéo. Il lui reste 450 dh .
- Quelle fraction de de son argent de poche représente l’ensemble des dépenses ?
- Quelle fraction de son argent de poche représente ce qui lui reste?
- Déterminer le nombre $x$ tel que : $\dfrac{5}{24} \times x=450$. Que peut-on conclure?

$x$ et $y$ sont deux nombres rationnels non nuls tels que: $$x+y\neq 0 \quad;\quad x-y\neq 0 \quad et \quad \dfrac{1-x}{y-x}=\dfrac{1}{y+x}$$
Montrer que : $x+y=2$
I. Addition de deux nombres rationnels
Pour additionner deux nombres rationnels de même dénominateur, on additionne les numérateurs entre eux et on garde le dénominateur commun.
Exemples:
$$\begin{aligned}
\mathbf{1.}\quad A&=\frac{-8}{3}+\frac{2}{3}\\
A&=\frac{-8+2}{3}\\
&=-\frac{6}{3}=-2
\end{aligned} \quad\quad
\begin{aligned}
\mathbf{2.}\quad B&=\dfrac{x}{2}+\dfrac{-5}{2}\\
B&=\frac{x+(-5)}{2} \\
B&=\frac{x-5}{2}
\end{aligned}
$$
Pour additionner deux nombres rationnels de dénominateurs différents, on commence par les écrire avec le même dénominateur et on applique la règle précédente.
Exemples :
$$
\begin{aligned}\textbf{ 1. }\quad
A & =\frac{-5}{9}+\frac{1}{3} \\
A & =\frac{-5}{9}+\frac{3}{9} \\
A & =\frac{-5+3}{9} \\
A & =\frac{-2}{9}
\end{aligned}\quad\quad
\begin{aligned}\textbf{ 2. }\quad
B & =\frac{7}{15}+\frac{-5}{6} \\
B & =\frac{14}{30}+\frac{-25}{30} \\
B & =\frac{14+(-25)}{30} \\
B & =\frac{-11}{30}
\end{aligned}
$$
- $\dfrac{a}{b}$ est un nombre rationnel : $\dfrac{a}{b}+\left(-\dfrac{a}{b}\right)=0$
On dit que:
$\quad\bullet~~ -\dfrac{a}{b}$ est l’opposé de $\dfrac{a}{b}$.
$\quad\bullet~~ -\dfrac{a}{b}$ et $\dfrac{a}{b}$ sont deux nombres opposés. - $\dfrac{a}{b}$ est un nombre rationnel : $\dfrac{a}{b}+0=\dfrac{a}{b}$
- $\dfrac{a}{b}$ et $\dfrac{c}{d}$ sont deux nombres rationnels : $\dfrac{a}{b}+\dfrac{c}{d}=\dfrac{c}{d}+\dfrac{a}{b}$
- $x, y$ et $z$ sont des nombres rationnels :
$$
\begin{aligned}
x+y+z & =(x+y)+z \\
& =x+(y+z) \\
& =(x+z)+y
\end{aligned}
$$
II. SOUSTRACTION
$$
\begin{aligned}
\frac{a}{b}-\frac{c}{d} & =\frac{a}{b}+\frac{-c}{d} \\
& =\frac{a d}{b d}+\frac{-b c}{b d} \\
& =\frac{a d+(-b c)}{b d} \\
& =\frac{a d-b c}{b d}
\end{aligned}
$$
Donc : $\dfrac{a}{b}-\dfrac{c}{d}=\dfrac{ad-bc}{bd}$
Exemples:
$$
\begin{aligned}
\textbf {1.}\quad A & =\frac{-28}{3}-\frac{5}{3} \\
A & =\frac{-28}{3}-\frac{5}{3} \\
A & =\frac{-28-5}{3} \\
A & =\frac{-33}{3} \\
A & =-11
\end{aligned}\quad\quad
\begin{aligned}
\textbf {2.}\quad B & =\frac{-3}{4}-\frac{7}{6} \\
B & =\frac{-3}{4}-\frac{7}{6} \\
B & =\frac{-9}{12}-\frac{14}{12} \\
B & =\frac{-9-14}{12} \\
B & =\frac{-23}{12}
\end{aligned}
$$
III. PRODUIT DE DEUX NOMBRES RATIONNELS
- on multiplie les numérateurs entre eux;
- on multiplie les dénominateurs entre eux .
Exemples :
$\quad \begin{aligned}
\textbf{1.}\quad A&=\dfrac{9}{5} \times \dfrac{2}{7}\\
A&=\dfrac{9 \times 2}{5 \times 7} \\
A&=\dfrac{18}{35}
\end{aligned}$
$\quad\begin{aligned}
\textbf{2.}\quad B&=4 \times \dfrac{11}{13}\\
B&=\dfrac{4 \times 11}{13}\\
B&=\dfrac{44}{13}
\end{aligned}$
$\quad\begin{aligned}
\textbf{3.}\quad C&=\dfrac{5}{6} \times \dfrac{36}{25}\\
C&=\dfrac{5 \times 6 \times 6}{6\times 5\times 5} \\
C&=\dfrac{6}{5} .
\end{aligned}$
- $\quad\quad\dfrac{a}{b}$ est un nombre rationnel : $1 \times \dfrac{a}{b}=\dfrac{a}{b} \quad$ et $\quad \dfrac{a}{b} \times 0=0$
- $\quad\quad\dfrac{a}{b}, \dfrac{c}{d}$ et $\dfrac{e}{f}$ sont des nombres rationnels :
$$
\begin{aligned}
\bullet & \dfrac{a}{b} \times \frac{c}{d}=\frac{c}{d} \times \frac{a}{b} \\
\bullet & \frac{a}{b} \times \frac{c}{d} \times \frac{e}{f}=\left(\frac{a}{b} \times \frac{c}{d}\right) \times \frac{e}{f}=\frac{a}{b} \times\left(\frac{c}{d} \times \frac{e}{f}\right)
\end{aligned}
$$
Exemple: $$\begin{aligned}
\frac{3}{5} \times \frac{7}{8} \times \frac{5}{9} & =\frac{3}{5} \times \frac{5}{9} \times \frac{7}{8} \\
& =\frac{3}{1} \times \frac{1}{9} \times \frac{7}{8}=\frac{1}{3} \times \frac{7}{8}=\frac{7}{24}\end{aligned}$$
IV. QUOTIENT DE DEUX NOMBRES RATIONNELS
1. Inverse d’un nombre rationnel non nul.
D’où: $\dfrac{1}{\dfrac{a}{b}}=\dfrac{b}{a} \quad$ et $\quad\left(\dfrac{a}{b}\right)^{-1}=\dfrac{b}{a}$.
Exemples:
- $-3 \times \dfrac{1}{-3}=1$, donc $\dfrac{1}{-3}$ est l’inverse de $-3$.
- $4 \times 0,25=1$, donc $4$ est l’inverse de $0,25$.
- $0,5 \times 2=1$, donc $0,5$ est l’inverse de $2$.
2. Quotient de deux nombres rationnels
Le quotient de $\dfrac{a}{b}$ par $\dfrac{c}{d}$ est le produit de $\dfrac{a}{b}$ par l’inverse de $\dfrac{c}{d}$.
Exemples :
- $-\dfrac{8}{5}\div \dfrac{4}{3}=-\dfrac{8}{5} \times \dfrac{3}{4}=-\dfrac{4 \times 2 \times 3}{5 \times 4}=-\dfrac{6}{5}$
- $\dfrac{9}{11}\div (-4)=\dfrac{9}{10} \times\left(\dfrac{-1}{4}\right)=\dfrac{-9}{40}$

Simplifier les nombres suivants : $$\dfrac{-72}{54} \quad et \quad \dfrac{165}{75}$$

Réduire les nombres rationnels $\dfrac{6}{5}$ et $\dfrac{17}{25}$ au même dénominateur.

Réduire les nombres rationnels $\dfrac{5}{24}$ et $\dfrac{-7}{32}$ au meme dénominateur.

Déterminer le nombre qui manque : $\dfrac{15}{27}=\dfrac{-30}{\cdots}$

Montrer que les nombres rationnels $\dfrac{45}{60}$ et $\dfrac{63}{84}$ sont égaux.

$a$, $b$, $c$ et $d$ sont des nombres rationnels tels que : $b\neq 0$, $d\neq 0$, $b+d\neq 0$ et $\dfrac{a}{b}=\dfrac{c}{d}.$
Montrer que : $\dfrac{a}{b}=\dfrac{a+c}{b+d}.$

$x$ et $y$ sont deux nombres rationnels tels que : $\dfrac{x}{y}=\dfrac{2}{3}$ et $x+y=-5$
Déterminer $x$ et $y$.

Déterminer les nombres entiers relatifs $x$ tels que : $$\dfrac{26}{27}<\dfrac{x}{54}<\dfrac{7}{6}$$

Un robinet A remplit un bassin en 4 heures.
Un robinet B le remplit en 6 heures.
A 9h30min, on ouvre le robinet A.
Dès que le bassin est à moitié plein, on ouvre le robinet B.
A quelle heure le bassin sera-t-il plein?
Nombre rationnel
Où $a$ est le nombre numérateur et $b$ est le dénominateur.
- Le nombre $\dfrac{3}{7}$ est un nombre rationnel, car $3$ et $7$ sont des nombres relatifs.
- Le nombre $\pi$ n’est pas un nombre rationnel.
Règle de simplification d’un nombre rationnel
$$\dfrac{a}{b}=\dfrac{a\times k}{b\times k} \quad et \quad
\dfrac{a}{b}=\dfrac{a\div k}{b\div k}$$
Règle des signes
- Le quotient de deux nombres de même signe est un nombre positif.
- Le quotient de deux nombres de signes contraires est un nombre négatif.
$$\dfrac{-a}{-b}=\dfrac{a}{b} \quad et \quad \dfrac{a}{-b}=\dfrac{-a}{b}=-\dfrac{a}{b}$$
Egalité de deux nombres rationnels
- Si $\dfrac{a}{b}=\dfrac{c}{d}$, alors : $a\times d=b\times c.$
- Si $a\times d=b\times c$, alors : $\dfrac{a}{b}=\dfrac{c}{d}$.
- Montrons que les nombres $\dfrac{8}{9,6}$ et $\dfrac{1,2}{1,44}$ sont égaux.
1ère méthode : Comparons d’abord : $$8\times 1,44 \,\,\,\text{ et }\,\,\, 9,6\times 1,2$$On a : $$8\times 1,44=11,52\,\,\,\text{ et }\,\,\,9,6\times 1,2=11,52$$Donc : $$8\times 1,44=9,6\times 1,2$$D’où : $$\dfrac{8}{9,6}=\dfrac{1,2}{1,44}$$2ème méthode : On a : $$\dfrac{8}{{9,6}} = \dfrac{{80}}{{96}} = \dfrac{{5 \times 16}}{{6 \times 16}} = \dfrac{5}{6}\,\,\,\text{ et }\,\,\,\dfrac{{1,2}}{{1,44}} = \dfrac{{120}}{{144}} = \dfrac{5}{6}$$Donc : $$\dfrac{8}{9,6}=\dfrac{1,2}{1,44}$$ - Montrons que les nombres $\dfrac{15}{4,8}$ et $\dfrac{6}{1,9}$ ne sont pas égaux.
Comparons d’abord : $$15\times 1,9\,\,\,\text{ et }\,\,\, 4,8\times 6$$On a : $$15\times 1,9=28,5\,\,\,\text{ et }\,\,\,4,8\times 6=28,8$$Donc : $$15\times 1,9\neq 4,8\times 6$$D’où : $$\dfrac{15}{4,8}\neq \dfrac{6}{1,9}$$
Réduire au même dénominateur
- $\dfrac{-3}{8}=\dfrac{-3 \times 3}{8 \times 3}=-\dfrac{9}{24}$
- $\dfrac{7}{6}=\dfrac{7 \times 4}{6 \times 4}=\dfrac{28}{24}$

Calculer : $$A=12\div (10-4)+5\times 14-8$$

- Sans poser d’opération, calculer astucieusement le nombre : $$B=31,5\times 98$$
- Calculer de la manière la plus simple (sans utiliser la calculatrice) : $$C=3,9\times 7 + 3,9\times 3$$

Calculer le nombre $D$ donné par l’expression : $$D=64-(3+12\div 4)\times 8$$

Ahmed achète une boîte de rangement en bois à $5,20$DH, pour ranger huit tubes de peinture à $1,30$DH chacun et trois pinceaux à $1,55$DH le pinceau.
Ecrire le montant des achats à l’aide d’une seule expression, puis la calculer.

Soit $a, b$ et $c$ des nombres entiers tels que :
$$
\left\{\begin{array}{l}
a \times b=6 \\
a \times c=10 \\
b+c=8
\end{array}\right.
$$
Calculer $a$ , $b$ et $c$.
I. Calculs sans parenthèses
1. Avec des additions et des soustractions
Exemple :
\[\begin{aligned}
A &= 39 – 14 + 5 – 9\\
&= 25 + 5 – 9\\
&= 30 – 9\\
&= 21
\end{aligned}\]
\[\begin{aligned}
B &= 7,8 – 5,2 + 3,4\\
&= 2,6 + 3,4\\
&= 6
\end{aligned}\]
2. Avec des multiplication et des divisions
Exemple :
\[\begin{aligned}
C &= 48 \div 8 \times 3 \div 9\\
&= 6 \times 3 \div 9\\
&= 18 \div 9\\
&= 2\\
D &= 5 \times 8 \div 10\\
&= 40 \div 10\\
&= 4
\end{aligned}\]
3. Avec des additions, des soustractions et des multiplication ou des divisions
Exemple :
\[\begin{aligned}
E &= 8 + 5 \times 3 – 10 \div 2\\
&= 8 + 15 – 5\\
&= 23 – 5\\
&= 18
\end{aligned}\]
II. Calculs avec parenthèses
Quand il y a plusieurs niveaux de parenthèses, on commence par effectuer les calculs dans les parenthèses intérieurs.
Exemple :
\[\begin{aligned}
F &= 97 – \left[ {6 \times \left( {4 + 5} \right) – 10} \right]\\
&= 97 – \left[ {6 \times 9 – 10} \right]\\
&= 97 – \left[ {54 – 10} \right]\\
&= 97 – 44\\
&= 53
\end{aligned}\]
III. Distributivité de la multiplication par rapport à l’addition et à la soustraction
$$\begin{aligned}
\bullet\quad k\times (a+b)=k\times a+k\times b\\
\bullet\quad k\times (a-b)=k\times a-k\times b\\
\end{aligned}$$
On dit que la multiplication est distributive par rapport à l’addition et à la soustraction.
- Produit transforme en somme : $k\times (a+b)=k\times a+k\times b$
- Somme transforme en produit : $k\times a+k\times b=k\times (a+b)$
Exemple :
- Calculons de deux facons l’expression : $E=8\times (17-4)$
1ère méthode : \[\begin{aligned}
E &= 8 \times \left( {17 – 4} \right)\\
&= 8 \times 13\\
&= 104
\end{aligned}\]2ème méthode :\[\begin{aligned}
E &= 8 \times \left( {17 – 4} \right)\\
&= 8 \times 13 – 8 \times 4\\
&= 136 – 32\\
&= 44
\end{aligned}\] - Soit $a$ un nombre décimal, réduisons l’expression : $F=5\times a+3\times a$
\[\begin{array}{l}
F = 5 \times a + 3 \times a\\
= \left( {5 + 3} \right) \times a\\
= 8 \times a
\end{array}\]
IV. Conventions d’écriture
- Entre deux lettres
- Devant une parenthèse
- Entre un nombre et un lettre.
Exemple :
- $k\times a=ka$
- $6\times y=6y$
- $5\times(4+x)=5(4+x)$
- $3 \times 4$ reste $3 \times 4$ et ne s’écrit pas « $34$ »
- $1 \times x$ peut s’écrit $x$.

Sans calculatrice, donner la valeur exacte des nombres suivants :
\begin{array}{ll}
\mathbf{1.}\ A = \sqrt {1000000}&\quad\mathbf{2.}\ B = \dfrac{{\sqrt 9 + \sqrt {121} }}{{\sqrt {49} }}\\
\mathbf{3.}\ C = \sqrt {\dfrac{{50}}{{98}}}&\quad\mathbf{4.}\ D = \sqrt {31 + \sqrt {21 + \sqrt {9 + \sqrt {49} } } }\\
\end{array}

Simplifier et calculer :
\begin{array}{ll}
\mathbf{1.}\ A = \sqrt {50} &\quad\mathbf{2.}\ B = \sqrt {363}\\
\mathbf{3.}\ C = 5\sqrt {27} &\quad\mathbf{4.}\ D = \sqrt {24} + 7\sqrt 6 + 2\sqrt {54}\\
\mathbf{5.}\ E = \sqrt 3 \times \sqrt {21} \times \sqrt 7 &\quad\mathbf{6.}\ F = \sqrt {{5^3} \times {7^5} \times 1000}\\
\mathbf{7.}\ G = \sqrt {242} \times \sqrt {128} &\quad\mathbf{8.}\ H = \sqrt 7 \left[ {\sqrt {700} + {{\left( {\sqrt 7 } \right)}^3}} \right]\\
\mathbf{9.}\ I = \left( {\sqrt {13} – 5} \right)\left( {\sqrt {13} + 5} \right) &\quad\mathbf{10.}\ J = {\left( {\sqrt 5 + 2} \right)^2} \\
\mathbf{11.}\ K = {\left( {\sqrt 3 – 1} \right)^4} &\quad\mathbf{12.}\ L = \left( {\sqrt 3 + 5} \right)\left( {2\sqrt 3 + 1} \right)\\
\mathbf{13.}\ M = \sqrt {{{\left( {\sqrt 7 – 3} \right)}^2}} &\quad\mathbf{14.}\ N = \sqrt {{{\left( {\sqrt 5 – 1} \right)}^2}} + \sqrt {{{\left( {\sqrt 5 – 7} \right)}^2}}\ \\
\mathbf{15.}\ O = \sqrt {3 + 2\sqrt 2 } &\quad\mathbf{16.}\ P = \sqrt {8 – 2\sqrt {12} }\\
\end{array}

Écrire sans « $\sqrt{~~}$ » au dénominateur.
\begin{array}{ll}
\mathbf{1.}\ A = \dfrac{3}{{\sqrt 2 – 1}} &\quad\mathbf{2.}\ B = \dfrac{{\sqrt 5 – 3}}{{\sqrt 5 }}\\
\mathbf{3.}\ C = \dfrac{5}{{\sqrt 7 – 2}} – \dfrac{2}{{\sqrt 7 }} &\quad\mathbf{4.}\ D = \dfrac{{3 + \sqrt 5 }}{{7 + \sqrt 5 }} – \dfrac{{3 – \sqrt 5 }}{{7 – \sqrt 5 }}\\
\mathbf{5.}\ E = \dfrac{{\sqrt 2 + \sqrt 3 }}{{\sqrt 5 – \sqrt 7 }} &\quad\mathbf{6.}\ F = \dfrac{1}{{1 + \sqrt 2 + \sqrt 3 }}\\
\end{array}
Chapitre 3
Racine carrée d’un nombre positif
La racine carrée du nombre $a$ est le nombre dont le carrée est $a$, et se note $\sqrt{a}$.
On écrit : $\sqrt{a}^2=a$
Si $a=b^2$ signifie que $b=\sqrt{a}$
Exemples :
$\bullet\quad \sqrt{0}=0$
$\bullet\quad \sqrt{5}^2=5$
$\bullet\quad \sqrt{3^2}=3$
$\bullet\quad \sqrt{1}=1$
$\bullet\quad \sqrt{16}=\sqrt{4^2}=4$
$\bullet\quad \sqrt{(-7)^2}=\sqrt{7^2}=7$
$\bullet\quad \sqrt{\dfrac{100}{9}}=\sqrt{\left( \dfrac{10}{3}\right) ^2}=\dfrac{10}{3}$
$\bullet\quad \sqrt{2,12}=\sqrt{1,1^2}=1,1$
Racine carrée et produit
Exemples :
$\bullet$ $\sqrt{2}\times \sqrt{8}=\sqrt{2 \times 8}=\sqrt{16}=4$
$\bullet$ $\sqrt{80}=\sqrt{16 \times 5}=\sqrt{16}\times \sqrt{5}=\sqrt{4^2}\times \sqrt{5}=4\sqrt{5}$
$\bullet$ $\sqrt{2}\times \sqrt{6}\times \sqrt{8}=\sqrt{2 \times 6 \times 8}=\sqrt{96}=\sqrt{16 \times 6}=\sqrt{4^2 \times 6}=4\sqrt{6}$
Racine carrée et quotient
$$\dfrac{\sqrt{a}}{\sqrt{b}}=\sqrt{\dfrac{a}{b}}$$
Exemple :
$\bullet$ $\dfrac{\sqrt{12}}{\sqrt{3}}=\sqrt{\dfrac{12}{3}}=\sqrt{4}=\sqrt{2^2}=2$
$\bullet$ $\sqrt{\dfrac{25}{9}}=\dfrac{\sqrt{25}}{\sqrt{9}}=\dfrac{\sqrt{5^2}}{\sqrt{3^2}}=\dfrac{5}{3}$
$\bullet$ $\dfrac{\sqrt{32}}{\sqrt{2}}=\dfrac{\sqrt{16 \times 2}}{\sqrt{2}}=\dfrac{\sqrt{16}\times \sqrt{2}}{\sqrt{2}}=\sqrt{16}=\sqrt{4^2}=\sqrt{4}$
Rendre rationnel le dénominateur d’un nombre réel
$$\dfrac{a}{\sqrt{b}}=\dfrac{a\sqrt{b}}{\sqrt{b}^2}=\dfrac{a\sqrt{b}}{b}$$
Exemples : Écrire sans utiliser la racine ($\sqrt{~~}$) au dénominateur.
$\bullet$ $\dfrac{2}{\sqrt{5}}=\dfrac{2\sqrt{5}}{\sqrt{5}^2}=\dfrac{2\sqrt{5}}{5}$
$\bullet$ $\dfrac{\sqrt{3}}{5\sqrt{2}}=\dfrac{\sqrt{3} \times \sqrt{2}}{5\sqrt{2}^2}=\dfrac{\sqrt{6}}{10}$
$$\begin{equation*}
\dfrac{a}{\sqrt{a}+\sqrt{b}}=\dfrac{a\left( \sqrt{a}-\sqrt{b} \right)}{\left( \sqrt{a}+\sqrt{b} \right)\left( \sqrt{a}-\sqrt{b} \right)}=\dfrac{a\left( \sqrt{a}-\sqrt{b} \right)}{\sqrt{a}^2-\sqrt{b}^2}=\dfrac{a\left( \sqrt{a}-\sqrt{b} \right)}{a-b}
\end{equation*}$$
Exemples : Écrire sans utiliser la racine ($\sqrt{~~}$) au dénominateur.
$\bullet$ $\dfrac{2}{1-\sqrt{5}}=\dfrac{2(1+\sqrt{5})}{(1-\sqrt{5})(1+\sqrt{5})}=\dfrac{2(1+\sqrt{5})}{1^2-\sqrt{5}^2}=\dfrac{2(1+\sqrt{5})}{1-5}=\dfrac{2(1+\sqrt{5})}{-4}$
$\bullet$ Les nombres $1+\sqrt{5}$ et $1-\sqrt{5}$ sont dits conjuguées.
L’équation $x^2=a$
$\bullet$ Si $a=0$, alors l’équation $x^2=a$ a une seule solution : $0$
$\bullet$ Si $a>0$, alors l’équation $x^2=a$ a deux solutions : $\sqrt{a}$ et $-\sqrt{a}$
$\bullet$ Si $a<0$, alors l’équation $x^2=a$ n’a pas de solution.
Exemples :
$\bullet$ L’équation $x^2=3$, a deux solutions : $\sqrt{3}$ et $-\sqrt{3}$
$\bullet$ L’équation $x^2=16$, a deux solutions : $4$ et $-4$
$\bullet$ L’équation $x^2=0$, a une seule solution : $0$.
$\bullet$ L’équation $x^2=-25$, n’a pas de solution car $-25<0$.





