Chapitre 4
Puissance d’exposant positif d’un nombre rationnel
$$a^{n}=\underbrace{a \times a \times \ldots \ldots \times a}_{n \text { facteurs }}$$
$\bullet$ Si $n=1$, alors $a^1=a$
$\bullet$ Si $n=0$ et $a \neq 0$ alors $a^0=1$
$\bullet$ Si $n\neq 0$ et $a = 0$ alors $0^n=0$
$\bullet$ $a$ est la base de la puissance $a^n$.
$\bullet$ $n$ est l’exposant de la puissance $a^n$.
$\bullet$ $0^0$ n’existe pas.
Exemples :
$\bullet$ $(-3)^4=(-3)\times(-3)\times(-3)\times(-3)=9 \times 9 = 81$
$\bullet$ $\left(\dfrac{-2}{3}\right)^3=\dfrac{-2}{3}\times\dfrac{-2}{3}\times \dfrac{-2}{3}=\dfrac{-2\times 2\times 2}{3\times 3\times 3}=\dfrac{-8}{27}$
$\bullet$ $2019^0=1$
$\bullet$ $523^1=523$
Puissance d’exposant négatif d’un nombre rationnel
Soit $a$ un nombre rationnel non nul, $n$ un nombre entier naturel. $$a^{-n}=\dfrac{1}{a^n}$$
$\bullet$ La puissance $a^{-n}$ est l’inverse de la puissance $a^n$.
$\bullet$ Si $\dfrac{a}{b}$ un nombre rationnel non nul, alors $\left(\dfrac{a}{b}\right)^{-n}=\left(\dfrac{b}{a}\right)^{n}$.
Exemples :
$\bullet$ $2^{-3}=\dfrac{1}{2^3}=\dfrac{1}{2\times 2\times 2}=\dfrac{1}{8}$
$\bullet$ $\left(\dfrac{3}{5}\right)^{-2}=\left(\dfrac{5}{3}\right)^{2}=\dfrac{5}{3}\times \dfrac{5}{3}=\dfrac{25}{9}$
$\bullet$ $\bigg[\left(\dfrac{2}{7}\right)^{-3}\bigg]^{-1}=
\bigg[\left(\dfrac{7}{2}\right)^{3}\bigg]^{-1}=
\bigg[\dfrac{7}{2}\times \dfrac{7}{2}\times\dfrac{7}{2}\bigg]^{-1}=
\bigg[\dfrac{343}{8}\bigg]^{-1}=\dfrac{8}{343}$
Le signe d’une puissance
- Si $n$ est pair, alors $a^n$ est toujours positif quel que soit le signe de $a$.
- Si $n$ est impair, alors $a^n$ et $a$ ont le meme signe.
Exemples :
$\bullet$ La puissance $\left( -12 \right)^{17}$ est \textbf{négatif}, car l’exposant est impaire et la base est négatif.
$\bullet$ La puissance $\left( -3 \right)^{48}$ est \textbf{positif}, car l’exposant est paire.
Opérations sur les puissances :
$\bullet\quad a^n \times a^m = a^{n+m}$ $\quad$ $\bullet\quad a^n \times b^n = (a \times b )^{n}$ $\quad$ $\bullet\quad \dfrac{a^n}{a^m}= a^{n-m}$ $\quad$ $\bullet\quad \dfrac{a^n}{b^n}= \left(\dfrac{a}{b}\right)^{n}$ $\quad$ $\bullet\quad \left( a^n\right)^m=a^{n\times m}$
Exemples :
$\bullet$ ${(-3)}^9 \times {(-3)}^5= {(-3)}^{9+5}={(-3)}^{14}$
$\bullet$ $2^{{7}} \times 5^{{7}}= (2 \times 5)^{{7}}=10^{{7}}$
$\bullet$ $\dfrac{{1,3}^8}{{1,3}^3}={1,3}^{8-3}={1,3}^5$
$\bullet$ $\dfrac{21^{{13}}}{7^{{13}}}=\left(\dfrac{21}{7}\right)^{{13}}=3^{{13}}$
$\bullet$ $\left({2}^3\right)^4={2}^{3 \times 4} ={2}^{12}$
Puissances de 10
$\bullet$ ${10^n} = 1\underbrace {00………0}_{n\,\,\text{zéros}}$
$\bullet$ ${10^{-n}} = \underbrace {0,00………0}_{n\,\,\text{zéros}}1$
$\bullet$ $10^0=1$ ; $10^1=10$ ; $10^{-n}=\dfrac{1}{10^n}$
Exemples :
$\bullet$ $1000000000=10^9$
$\bullet$ $10^5=100000$
$\bullet$ $0,000001=10^{-6}$
$\bullet$ $10^{-4}=0,0001$
$\bullet$ $10^8 \times 10^3=10^{8+3}=10^{11}$
$\bullet$ $\dfrac{10^6}{10^2}=10^{6-2}=10^4$
$\bullet$ $(10^5)^7=10^{5\times 7}=10^{35}$
Écriture scientifique
L’écriture scientifique de $x$ est :
$$x=a \times 10^{n} \text{~~ou~~} x=- a \times 10^{n}$$
Avec $1 \leq a < 10$.
Exemples :
$\bullet$ $649,2=6,492 \times 10^2$
$\bullet$ $-0,0000327=-3,27\times 10^{-5}$
$\bullet$ $32000000=3,2\times 10^{-7}$
$\bullet$ $569,4 \times 10^{13}=5,694 \times 10^2 \times 10^{13}=5,694\times 10^{15}$

- Ecrire sous forme d’une fraction les nombres suivants: $$3,1 \quad;\quad 4\quad;\quad \dfrac{0,02}{5,2}$$
- Compléter les égalités suivantes: $$\dfrac{\ldots}{42}=\dfrac{2}{7} \quad;\quad \dfrac{8}{16}=\dfrac{3}{\ldots}\quad;\quad \dfrac{\ldots}{5}=\dfrac{12}{20}=\dfrac{18}{\ldots}$$

Donner la forme irréductible des fractions suivantes:$$\dfrac{116}{320} \quad;\quad \dfrac{150}{750} \quad;\quad \dfrac{27\times 16}{72} \quad;\quad\dfrac{54\times 64\times 8}{28\times 27\times 32}$$

Comparer les fractions suivantes:$$\dfrac{14}{17} \text{ et } \dfrac{16}{17} \quad;\quad\dfrac{5}{3} \text{ et } \dfrac{5}{2}\quad;\quad\dfrac{5}{4} \text{ et } \dfrac{9}{8}\quad;\quad\dfrac{3}{7} \text{ et } \dfrac{6}{11}$$

Comparer les fractions : $$\dfrac{987654321}{987654322}\quad et \quad\dfrac{123456789}{123456780}$$

Compléter par un entier naturel convenable: $$\dfrac{6}{4}<\dfrac{\ldots}{8}<\dfrac{7}{4}\quad;\quad\dfrac{3}{7}<\dfrac{\ldots}{14}<\dfrac{4}{7}\quad;\quad\dfrac{9}{7}<\dfrac{3}{\ldots}<\dfrac{9}{5}$$

Soit $a$, $b$ et $c$ des nombres fractionnaires tels que : $$\dfrac{b\times c}{a}=1 \quad;\quad \dfrac{c\times a}{b}=2 \quad;\quad \dfrac{a\times b}{c}=3$$Calculer : $a^2+b^2+c^2$.
Olympiades de mathématiques
Durée de réalisation : 2 heures
Date de passation : Vendredi 20 décembre 2019

$a$ et $b$ deux nombres rationnels strictement positifs.
Montrer que : $$\left( {\sqrt a + b} \right)\left( {\frac{{\sqrt a }}{a} + \frac{1}{b}} \right) \ge 4$$

On pose : $x=3$ et $y=1$ et $z=2$.
c’est-à-dire : $x = y + z$
donc : $x\left( {x- y} \right) = \left( {y + z} \right)\left( {x- y} \right)$
donc : ${x^2}- xy = xy + xz- {y^2}- yz$
donc : ${x^2}- xy- xz = xy- {y^2}- yz$
donc : $x\left( {x- y- z} \right) = y\left( {x- y- z} \right)$
Après la simplification on obtient $x=y$ d’où $3 = 1$
Trouver l’erreur, justifier la réponse.

$ABC$ un triangle rectangle en $A$, son aire est égale à $1$.
Soient $A’$ et $B’$ les points tels que:
- $A’$ est le symétrique de $A$ par rapport à la droite $(BC)$.
- $B’$ est le symétrique de $B$ par rapport à la droite $(AC)$.
- $C’$ est le symétrique de $C$ par rapport à la droite $(AB)$.
Calculer l’aire du triangle $A’B’C’$.

$ABC$ un triangle d’angle $\widehat A $ aigu. $E$ un point du segment $[AB]$ tel que $AB=3AE$, $I$ est le milieu du segment $[AC]$ et $D$ est l’intersection des deux droites $(EI)$ et $(BC)$.
Montrer que $C$ est le milieu du segment $[BD]$.
Olympiades de mathématiques
Durée de réalisation : 2 heures
Date de passation : Vendredi 22 novembre 2019

$a$ et $b$ deux nombres rationnels tels que : $a>2$ et $b>2$.
Montrer que : $a+b < ab$.

Après six interrogations en mathématiques, un éléve de la troisième année collége a eu la moyenne $12$.
Sachant que la moyenne des deux notes obtenues à la deuxieme et à la cinquième interrogations est $11$, quelle est la moyenne des notes obtenues aux interrogations qui restent, la première, la troisizime, la quatrième et la sixième?

$ABCD$ un carré et $M$ le milieu du segment $[AD]$.
$E$ un point du segment $[DC]$ et $F$ un point du segment $[AB]$.
Déterminer les positions des deux points $E$ et $F$ pour que la somme $BE+EF+FM$ prend la plus petite valeur possible.

$ABC$ un triangle rectangle en $A$. $D$ est le point d’intersection de la droite issue du point $A$ et perpendiculaire à la droite $(BC)$.
$I$ est le milieu du segment $[BD]$. $J$ est le milieu du segment $[AD]$.
Montrer que les deux droites $(CJ)$ et $(AI)$ sont perpendiculaires.
Les questions de cet examen sont liées à ce que vous avez déjà étudié dans les niveaux scolaires précédents et sont en rapport avec le programme d’études que vous suivrez durant l’année en cours.

Le tableau ci-dessous montre le nombre d’enfants par famille dans une tribu :
| Nombre d’enfants | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Nombre de familles | 15 | 40 | 64 | 25 | 56 | 22 | 12 |
Combien de familles ont quatre enfants ou plus?
- $28$
- $96$
- $85$
- $56$

Combien vaut l’expression suivante : $$P=(3x−5)−(5x+3)(3x – 5)- (5x + 3)(3x−5)−(5x+3)$$
- $P=-30$
- $P=4x$
- $P=4x- 30$
- $P=-16- 30x$

Dans le triangle rectangle $EFG$ représenté ci-dessous,
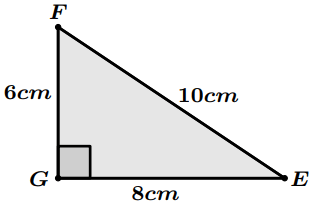
Calculer $\cos(\hat{GFE})$
- $\cos(\hat{GFE})=0,75$
- $\cos(\hat{GFE})=0,6$
- $\cos(\hat{GFE})=\dfrac{3}{4}$
- $\cos(\hat{GFE})=0,8$

Soit $x$ un nombre tel que $2,7 < x < 2,8$.
Parmi les expressions suivantes, laquelle est correcte?
- $2,4 < x- 3 < 2,5$
- $0,3 < x- 3 < 0,8$
- $-5,7 < x- 3 < -5,8$
- $-0,3 < x- 3 < -0,2$

Déterminer parmi les propositions suivantes lesquelles sont vraies :
- $-\dfrac{3}{2}$ est un nombre décimal.
- $\dfrac{1}{3}$ est un nombre rationnel.
- $-5,19$ est un nombre irrationnel.
- $\dfrac{2}{3}$ est un nombre décimal.

Dans le carré $PQRS$ de côté $5cm$, quelle est la longueur de la diagonale $[PR]$?
- $PR=\sqrt{5}cm$
- $PR=\sqrt{10}cm$
- $PR=\sqrt{40}cm$
- $PR=\sqrt{25}cm$

Le graphique ci-dessous représente une relation de proportionnalité entre les quantités d’un produit et leurs prix en dirhams.
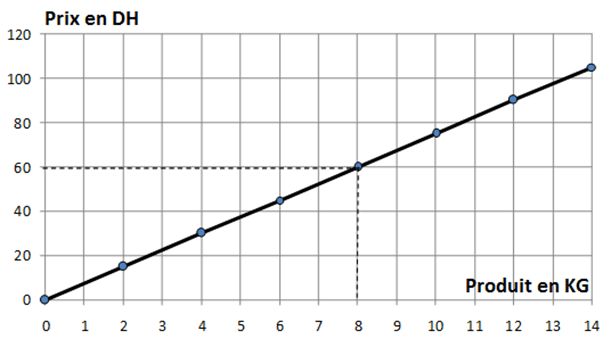
- $300$ dirhams
- $255$ dirhams
- $375$ dirhams
- $448$ dirhams

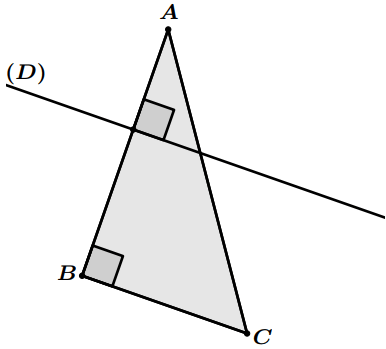
Construire le symétrique du triangle $ABC$ par rapport à la droite $(D)$, (en laissant les traces de la construction).

Cette année, l’âge de Ahmed est le double de celui de Ali, et l’âge de Souad est de 16 ans.
Quel est l’âge de Ahmed sachant que la somme des âges des trois personnes est de 88 ans?
- $50$ans.
- $40$ans.
- $48$ans.
- $35$ans.

Dans la figure suivante, $(EF)$ est parallèle à $(MN)$.
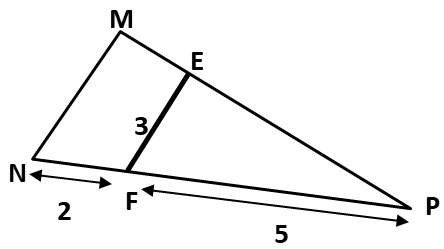
Quelle est la longueur du segment $[MN]$?
- $MN=\dfrac{21}{5}$
- $MN=\dfrac{6}{5}$
- $MN=\dfrac{5}{6}$
- $MN=\dfrac{25}{2}$

Quelle est l’écriture scientifique du nombre $0,000347$?
- $3,47\times 10^{-6}$
- $347\times 10^{-6}$
- $3,47\times 10^{-4}$
- $3,47\times 10^{-7}$

Place le point $N$ tels que $\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {BC}$. Laisse les traces de la construction.

Quel est la factorisation correcte de l’expression suivante: $A=(x + 3)(5x – 2) – (x + 3)(2x + 1)$?
- $A=(x+3)(3x-3)$
- $A=(x+3)(3x-1)$
- $A=(x+3)(-3x-3)$
- $A=(x+3)(7x-1)$

Combien vaut le nombre $B=\dfrac{2}{7}+\dfrac{3}{7}\times\dfrac{4}{5}-\dfrac{2}{3}$?
- $B=\dfrac{6}{35}$
- $B=\dfrac{10}{35}$
- $B=\dfrac{8}{35}$
- $B=\dfrac{16}{35}$

Dans la figure suivante :
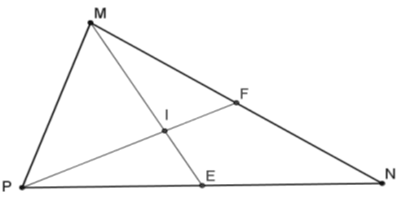
$E$ est le milieu de $[PN]$ et $F$ est le milieu de $[MN]$, et $I$ est le point d’intersection de $(ME)$ et $(PF)$ et $IF = 2 cm$.
Quelle est la longueur du segment $[PI]$?
- $PI=8cm$
- $PI=4cm$
- $PI=6cm$
- $PI=9cm$

Combien vaut le nombre $C=\dfrac{5^6}{36}\times\left(\dfrac{6}{5}\right)^2$?
- $C=6^2$
- $C=5^3$
- $C=6^4\times 5^7$
- $C=5^4$

La figure représente un parallélépipède rectangle $ABCDEFGH$ avec des dimensions de $8cm$, $6cm$ et $4cm$.
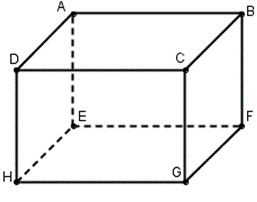
Quelle est la surface totale $\mathcal{S}_\mathcal{T}$ de ce solide?
- $\mathcal{S}_\mathcal{T}=208cm^2$
- $\mathcal{S}_\mathcal{T}=176cm^2$
- $\mathcal{S}_\mathcal{T}=192cm^2$
- $\mathcal{S}_\mathcal{T}=104cm^2$

Pendant la période de croissance d’une plante, sa longueur augmente de $7\%$ chaque semaine. Si sa longueur aujourd’hui est de $35cm$, quelle sera sa longueur après une semaine en centimètres?
- $30,37$
- $37,45$
- $35$
- $40$
Chapitre 8
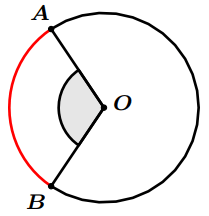
Angle au centre :
L’angle $\widehat{A O B}$ est appelé angle au centre qui intercepte l’arc $\overparen{A B}$.
Angle inscrit
- $A$, $B$ et $M$ trois points du cercle $(C)$.
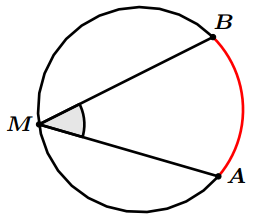
L’angle $\widehat{A M B}$ est appelé angle inscrit du cercle qui intercepte l’arc $\overparen{A B}$
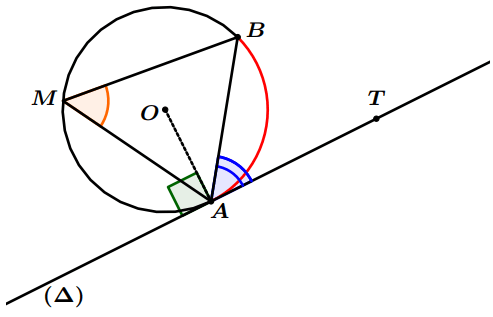
- Soit ( $\Delta$ ) la tangente du cercle $(C)$ au point $A$.
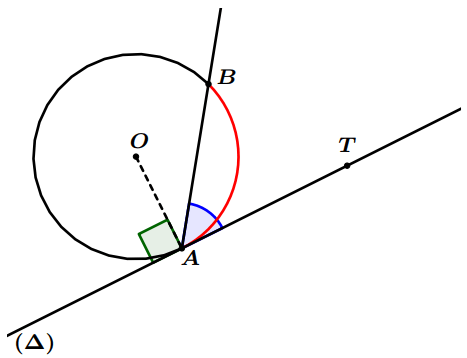
Angle inscrit et angle au centre associé
Exemple : Sur le dessin suivant :
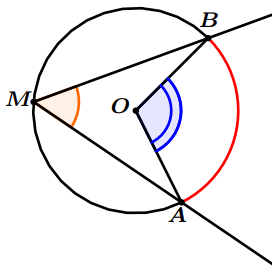
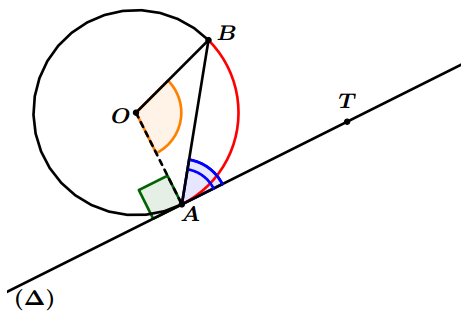
Angles inscrits interceptant le même arc
Exemple : Sur le dessin suivant :
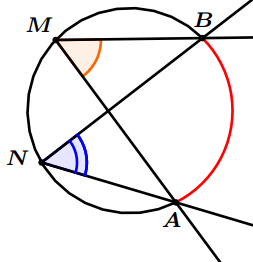
$\widehat{A M B}$ et $\widehat{A N B}$ sont deux angles inscrits qui interceptent le même arc donc : $\widehat{A M B}=\widehat{ANB}$.
Instructions pour le candidat
Durée de réalisation : 1 heure
Les questions de ce devoir sont issues des leçons suivantes :
- • Les identités remarquables
- • Les racines carrées
- • Les puissances

Soit $x$ un nombre réel. On pose :
$$A = 5\left( {x -2} \right) \quad;\quad B = {\left( {2x -1} \right)^2} + x\left( {2x -1} \right) \quad;\quad C = {\left( {x + 6} \right)^2} -25$$
- Développer et réduire : $A$, $B$ et $C$.
- Factoriser $B$ et $C$.

Écrire sous forme d’une seule puissance : $$D = \dfrac{{{a^{ -3}} \times {{\left( {a \times {a^{ -3}}} \right)}^{ -4}}}}{{{a^{ -1}} \times {a^{ -2}} \times a}}$$

- Donner l’écriture scientifique des nombres :
$$E = 0,048 \quad;\quad F=3000000$$ - En déduire l’écriture scientifique de:
$$G=\dfrac{0,048}{3000000}$$

Calculer et simplifier :
- $H = {\left( {\dfrac{{\sqrt 5 }}{2}} \right)^{ -2}} + \dfrac{7}{5}$
- $I = \sqrt {48} -\sqrt {12} + 2\sqrt 3 $
- $J = \sqrt {\dfrac{{\sqrt {100} -1}}{{{3^2} + {4^2}}}}$
- $K = \sqrt {\sqrt 5 -1} \times \sqrt {\sqrt 5 +1} $

Écrire sans « $\sqrt{~~}$ » au dénominateur :
- $L = \dfrac{{3}}{{7\sqrt 5 }}$
- $M = \dfrac{{\sqrt 3 }}{{\sqrt 3 -1}}$
Chapitre 7
Cosinus, sinus et tangente d’un angle aigu
Cosinus d’un angle aigu
$\cos \hat B= \dfrac{\text{longueur du côté adjacent à }\hat B}{\text{longueur de l’hpoténuse }}$
Exemple : Soit $ABC$ un triangle rectangle en $A$.
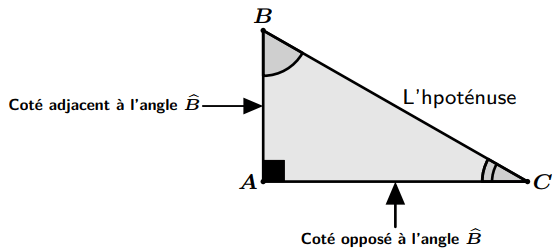
On a : $\boxed{\cos \widehat {ABC} = \frac{{AB}}{{BC}}}$ et $\boxed{\cos \widehat {ACB} = \frac{{AC}}{{BC}}}$
Sinus d’un angle aigu
$\sin \hat B= \dfrac{\text{longueur du côté opposé à }\hat B}{\text{longueur de l’hpoténuse }}$
Exemple : Soit $ABC$ un triangle rectangle en $A$.

On a : $\boxed{\sin \widehat {ABC} = \frac{{AC}}{{BC}}}$ et $\boxed{\sin \widehat {ACB} = \frac{{AB}}{{BC}}}$
Tangente d’un angle aigu
$\tan \hat B= \dfrac{\text{longueur du côté opposé à }\hat B}{\text{longueur du côté adjacent}\hat B}$
Exemple : Soit $ABC$ un triangle rectangle en $A$.

On a : $\boxed{\tan \widehat {ABC} = \frac{{AC}}{{AB}}}$ et $\boxed{\tan \widehat {ACB} = \frac{{AB}}{{AC}}}$
Formules trigonométries
- $0 < \cos \,\alpha \, < \,1$
- $0 < \sin \,\alpha \, < \,1$
- ${\cos ^2}\,\alpha \,\, + \,\,{\sin ^2}\,\alpha \,\, = \,\,1$
Preuve :
$\bullet$ Soit $ABC$ un triangle rectangle en $A$. On pose $\alpha=\widehat {ABC}$
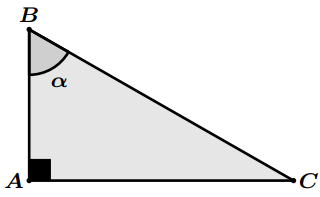
On a : $\sin \alpha= \dfrac{{AC}}{{BC}}$ et $\cos \alpha= \dfrac{{AB}}{{BC}}$
Nous savons que le plus long côté d’un triangle rectangle est l’hypoténuse,
C’est-à-dire : $0<AB<BC$ et $0<AC<BC $,
donc : $\dfrac{0}{BC}<\dfrac{AC}{BC}<\dfrac{BC}{BC}$ et $\dfrac{0}{BC}<\dfrac{AB}{BC}<\dfrac{BC}{BC}$
c’est-à-dire : $0<\sin \alpha<1$ et $0<\cos\alpha<1$.
$\bullet$ D’après le théorème de Pythagore, on a : $AC^2+AB^2=BC^2$,
Par suite, on a :
\[\begin{aligned}
{\sin ^2}\alpha + {\cos ^2}\alpha &= {\left( {\frac{{AC}}{{BC}}} \right)^2} + {\left( {\frac{{AB}}{{BC}}} \right)^2}\\
&= \frac{{A{C^2} + A{B^2}}}{{B{C^2}}}\\
&= \frac{{B{C^2}}}{{B{C^2}}}\\
&= 1
\end{aligned}\]
- ${\cos ^2}\alpha = 1-\sin^2 \alpha$
- ${\sin ^2}\alpha = 1-\cos^2 \alpha$
$${\tan}\alpha = \dfrac{\sin \alpha}{\cos \alpha}$$
- ${\cos}\alpha = \dfrac{\sin \alpha}{\tan \alpha}$
- ${\sin}\alpha = \cos\alpha\times\tan \alpha$
- $\cos \alpha = \sin \beta$
- $\sin \alpha = \cos \beta$
- $\tan \alpha = \dfrac{1}{\tan\beta}$
- $\cos\left( {90^\circ – \alpha } \right)= \sin\alpha$
- $\sin\left( {90^\circ – \alpha } \right) = \cos \alpha$
- $\tan\left( {90^\circ – \alpha } \right) = \dfrac{1}{\tan\alpha}$
Angles particuliers
| $x$ | $0^\circ$ | $30^\circ$ | $45^\circ$ | $60^\circ$ | $90^\circ$ |
| $\sin x$ | $0$ | $\dfrac{1}{2}$ | $\dfrac{\sqrt 2}{2}$ | $\dfrac{\sqrt 3}{2}$ | $1$ |
| $\cos x$ | $1$ | $\dfrac{\sqrt 3}{2}$ | $\dfrac{\sqrt 2}{2}$ | $\dfrac{\sqrt 1}{2}$ | $0$ |
| $\tan x$ | $0$ | $\dfrac{\sqrt 3}{3}$ | $1$ | $\sqrt 3$ | $***$ |
Chapitre 6
Théorème de Pythagore
$$AB^2+AC^2=BC^2.$$
Exemple :
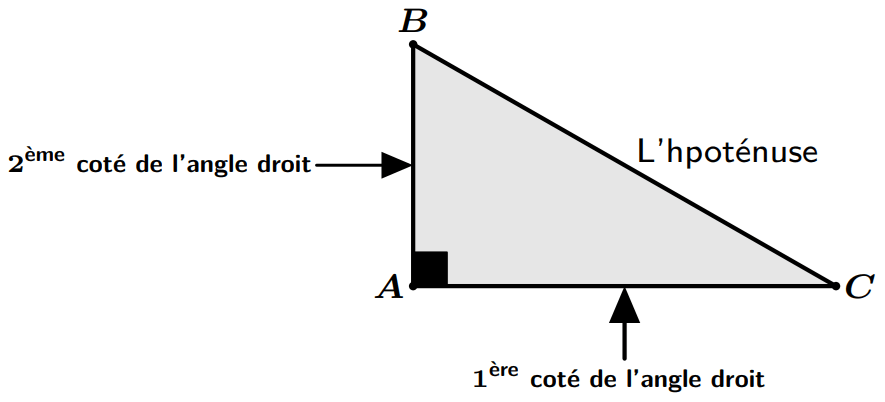
$$AB^2=BC^2-AC^2\quad et \quad AC^2=BC^2-AB^2.$$
Application : $EFG$ triangle rectangle en $E$ tel que :
$$EG = 2\sqrt{5}cm\quad ;\quad FG=6cm$$
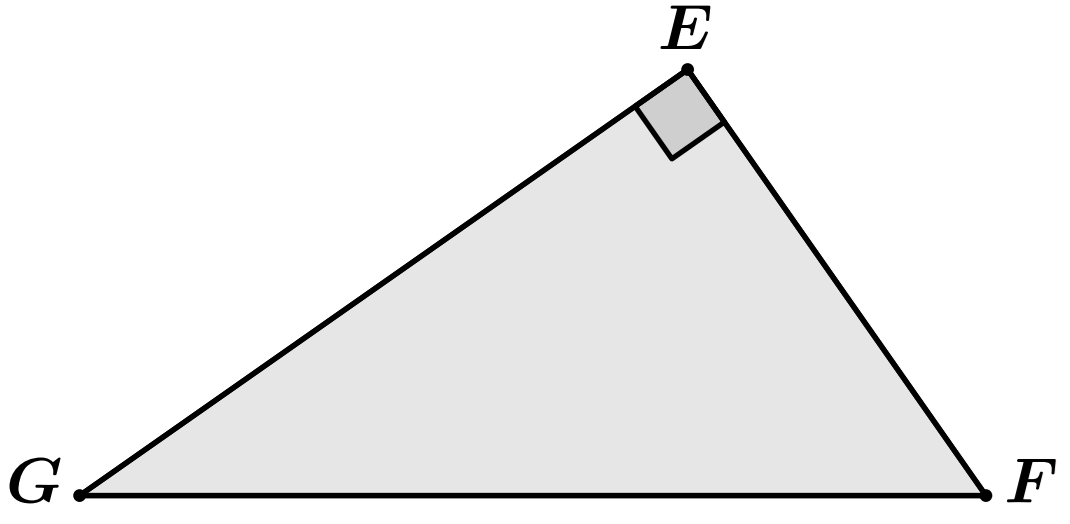
Réponse : Le triangle $EFG$ est rectangle en $E$.
Donc d’après le théorème de Pythagore on a :
$$E{F^2} + E{G^2} = F{G^2}$$
Alors :
$$\begin{aligned}
E{F^2} &= F{G^2} – E{G^2}\\
&= {6^2} – {\left( {2\sqrt 5 } \right)^2}\\
&= 36 – 4 \times 5\\
&= 36 – 20\\
&= 16
\end{aligned}$$
Puisque la distance est toujours positif, alors $\boxed{EF=\sqrt{16}cm=4cm}$
Réciproque du théorème de Pythagore
Application : Soit $ABC$ un triangle tel que :
$$AB=\sqrt{7}cm ~~;~~ AC = 2cm~~;~~BC=\sqrt{3}cm$$
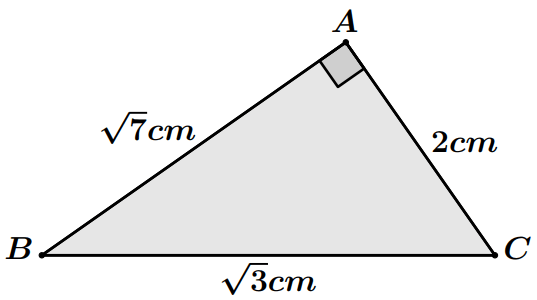
Réponse : On a : $AB^2=\sqrt{7}^2=7$; $AC^2=2^2=4$ et $BC^2=\sqrt{3}^2=3$
On remarque que : $4+3=7$
Ça veut dire que : $AC^2+BC^2=AB^2$
D’après la réciproque du théorème de Pythagore, le triangle $ABC$ est rectangle en $C$.

$x$ et $y$ sont deux nombres réels tels que: $2 \leq x \leq 3 \quad$ et $\quad 6 \leq y \leq 7$.
On considère l’expression $E$ : $$E=\sqrt{4 x^2-4 x y+y^2}+2 \sqrt{(x-3)^2+12 x}.$$
Donner une écriture simplifiée de $E$.

$a$ et $b$ sont deux nombres réels tels que: $a>1$ et $b>1$
Démontrer que : $$a \sqrt{b-1}+b \sqrt{a-1} \leq a b.$$

Soit $a$ et $b$ deux nombres réels tels que : $1 \leq \sqrt{a-3} \leq 3$ et $-4 \leq b \leq \dfrac{1}{2}$
- Montrer que : $4 \leq a<12$.
- Encadrer le nombre $\dfrac{3}{a}+b^2$.

$a$ et $b$ sont deux nombres réels positifs non nuls.
Montrer que : $$\dfrac{a}{a^4+b^2}+\dfrac{b}{a^2+b^4}\le \dfrac{1}{ab}.$$

$a$, $b$ et $c$ sont des nombres réels positifs non nuls.
Montrer que : $$\dfrac{ab}{c}+\dfrac{ac}{b}+\dfrac{bc}{a}\geq a+b+c.$$

$a$, $b$ et $c$ sont des nombres réels positifs non nuls.
Montrer que : $$\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\geq 9.$$

$a$ et $b$ sont deux nombres réels tels que : $a >1$ et $b>1.$
Montrer que : $$\dfrac{a^2}{b-1}+\dfrac{b^2}{a-1}\leq 8.$$

$x$ et $y$ sont deux nombres réels tels que : $$1\le x^2+y^2-xy\le 2.$$
Montrer que : $$\dfrac{2}{9}\le x^4+y^4\le 8.$$





