Démontrez les affirmations suivantes :
- Si $a$ et $b$ sont pairs, alors $a+b$ est pair.
- Si $a$ et $b$ sont impairs, alors $a+b$ est pair.
- Si $a$ est pair et $b$ est impair, alors $a+b$ est impair.
- Si $a$ et $b$ sont pairs, alors $ab$ est pair.
- Si $a$ et $b$ sont impairs, alors $ab$ est impair.
- Si $a$ est pair et $b$ est impair, alors $ab$ est pair.
- Si $a$ et $b$ sont deux nombres consécutifs, alors l’un est pair et l’autre est impair.

- Démontrez que si $a$ est pair, alors $a^2$ est pair.
- Démontrez que si $a$ est impair, alors $a^2$ est impair.
- En déduisez que si $a^2$ est pair, alors $a$ est pair, et si $a^2$ est impair, alors $a$ est impair.
- Démontrez que $\sqrt{2}\not\in \mathbb{Q}$.

Soit $a$ un nombre impair.
- Démontrez que $a^2-1$ est un multiple de $8$.
- En déduisez que $a^4-1$ est un multiple de $16$.
- Démontrez que si $m$ et $n$ sont des nombres impairs, alors $8$ divise $m^2+n^2+6$.

Soit $x\in \mathbb{N}$.
- Développez et simplifiez $(x+1)^2-x^2$.
- En déduisez que tout nombre impair est une différence de deux carrés parfaits.
- Écrivez le nombre $2005$ comme différence de deux carrés parfaits.
- On considère le nombre $a=n^2+n+7$ où $n\in \mathbb{N}$.
- Démontrez que le nombre $a$ est impair.
- En déduisez que le nombre $a$ est une différence de deux carrés parfaits.

Soit $m$ et $n$ de $\mathbb{N}$ tels que $m>n$.
- Démontrez que $m+n$ et $m-n$ ont la même parité.
- Déterminez les entiers naturels $x$ et $y$ qui satisfont $x^2-y^2=12$.

- Démontrez que : $a=3n^2+15n+7$ est un nombre impair.
- Démontrez que : $b=5n^2-7n+4$ est un nombre pair.
- Démontrez que : $c=n^4-n^2+16$ est un multiple de $4$.

Déterminez les entiers naturels $n$ qui vérifient $5n<32<5(n+1)$.

Déterminez le plus grand diviseur commun et le plus petit multiple commun des nombres $a$ et $b$ dans les cas suivants :
- $a=214$ et $b=816$
- $a=7371$ et $b=4095$
- $a=1959$ et $b=1963$

- Déterminez le nombre $a$ pour que le nombre $\overline {4a3a}$ soit divisible par $9$.
- Déterminez les nombres $a$ et $b$ pour que le nombre $\overline{65ab}$ soit divisible par $3$ et $4$.

Démontrez que pour tout entier naturel $n$, le nombre $\dfrac{n(n+1)(n+2)}{3}$ est un entier naturel.

- Démontrez que si $d$ divise $a$ et $b$, alors $d$ divise $ax+by$ pour tout $x$ et $y$ de $\mathbb{N}$.
- Démontrez que si $d$ divise $ab$ et $a+b$, alors $d$ divise $a^2$.
- Déterminez $\left( {{n^2} + n + 1} \right) \wedge \left( {n + 1} \right)$ pour tout $n\in \mathbb{N}$.
- Déterminez $\left( {{2^{n + 1}} – 1} \right) \wedge \left( {{2^n} – 1} \right)$ pour tout $n\in \mathbb{N}^*$.

Déterminez parmi les nombres suivants ceux qui sont premiers :
- $119$
- $503$
- $1559$
- $2523$
- $341$
- $2027$

Soit $n\in\mathbb{N}^*$.
- Démontrez que $n^3-n=(n+2)(n^2-2n+3)-6$.
- En déduisez les valeurs de $n$ pour que $\dfrac{n^3-n}{n+2}$ soit un entier naturel.

Soit $a\in\mathbb{N}$. Sachant que le reste de la division de $a$ par $12$ est $6$, quel est le reste de la division de $a$ par $4$, $3$, et $2$?

- Montrer que $\left(\forall(a, b) \in \mathbb{Z}^{2}\right): \,\,\, a \wedge b=1 \Rightarrow a \wedge b(a+b)=1.$
- Soient $x, y \in \mathbb{N}^{*}$ tels que : $x(43-x)=y(x+y)$. On pose $x \wedge y=d, x=d x^{\prime}, y=dy^{\prime}.$
- Montrer que $x^{\prime} \mid d$.
- On pose $\alpha=\dfrac{d}{x^{\prime}}$. Montrer que $\alpha\left(x^{\prime 2}+{x^{\prime}} y^{\prime}+y^{\prime 2}\right)=43$ et en déduire que $\alpha=1.$
- Résoudre dans $\mathbb{Z}^{* 2}$ l’équation $x(43-x)=y(x+y).$

Soient $k \in \mathbb{N}^{*},$ $A=9(k+3),$ $B=4 k,$ $d=A \wedge B$
- Montrer que $d\mid 108$.
- Déterminer les valeurs de $k$ pour lesquelles on a :
- $2$ ne divise pas $d$
- $3$ ne divise pas $d.$
- Soit $k=2+6m$.
- Montrer que $d=1.$
- Résoudre dans $\mathbb{Z}^{2}$ l’équation $A x-B y=108.$

On pose $A_{n}=6 n^{3}-n^{2}+2 n+2$, $B_{n}=2 n-1$, $C_{n}=2 n^{2}+n-5$. $n$ étant un entier relatif tel que les nombres $A_{n}$, $B_{n}$, $C_{n}$ soient non nuls.
- Montrer que : $A_{n} \wedge B_{n}=(n+1) \wedge 7$.
- Déterminer suivant les valeurs de $n A_{n} \wedge B_{n}$.
- Montrer que : $C_{n} \wedge B_{n}=B_{n} \wedge 6$.
- Déterminer suivant les valeurs de $n C_{n} \wedge B_{n}$.

- Soient $a, b \in \mathbb{N}$. Montrer que : $a \wedge b=1 \Rightarrow(a+2 b) \wedge(3 a+5 b)=1$.
- Résoudre dans $\mathbb{N}^{2}$ le système $\left\{\begin{array}{l}(a+2 b)(3 a+5 b)=127 b \\ a b=2(a \vee b)\end{array}\right.$

Soient $a, b, c, d \in \mathbb{N}^{*}$
- Montrer que $a \wedge(b \vee a)=a$ et $a \vee(b \wedge a)=a$.
- Montrer que si $a \wedge b=1$ alors $a \wedge(b c)=a \wedge c$ et $a \vee(b c)=b(a \vee c)$.
- Montrer que $\left(a^{2}+b^{2}\right) \wedge(a b)=(a \wedge b)^{2}$.
- Montrer que $a \wedge b=(a+b) \wedge(a \vee b)$.

Soient $a, b, m, n \in \mathbb{N}$
- Montrer que : $(a \equiv b[n]$ et $d\mid n) \Rightarrow a \equiv b[d]$
- Montrer que : $(a \equiv b[n]$ et $a \equiv b[m]) \Leftrightarrow a \equiv b[m \vee n]$
- En déduire que si $a \equiv a^{5}[5]$ alors $a$ et $a^{5}$ ont la même unité dans leur écriture en base $10$.

Soit $n$ un entier tel que $n>5$.
- On suppose qu’il existe un entier naturel $m$ tel que $(n-1)!+1=n^{m}$
- Montrer que $n$ est un impaire.
- Montrer que $(n-1)^{2} /(n-1)!$.
- Montrer que $(n-1) \mid m$.
- En déduire que $n^{m}>(n-1)!+1$.
- Montrer qu’il n’existe pas d’entiers naturels tel que : $(n-1)!+1=n^{m}$.

Soit $n \in \mathbb{N}^{*}-\{1\}$. On pose $M_{n}=2^{n}-1$
- Montrer que si $M_{n}$ est premier alors $n$ est aussi premier.
- Soient $p, q \in \mathbb{N}^{*}-\{1\}$ tels que : $p \wedge q=1$
- Montrer que: $\left(\exists(x, y) \in \mathbb{N}^{2}\right): p x-q y=1$
- Montrer que : $\left(2^{p x}-1\right)-2\left(2^{p y}-1\right)=1$
- En déduire que : $M_{p} \wedge M_{q}=1$

On considère dans $\mathbb{N}^{2}$ l’équation $x^{2}+3=2^{y}$. Soit $(x, y)$ une solution de cette équation.
- Montrer que $x$ est impaire.
- Montrer que $x^{2} \equiv 1[8]$.
- En déduire les solutions de cette équation.

On considère dans $\mathbb{N}^{3}$ l’équation $\,(E):\,\,\, x^{2}+2 y^{2}=z^{2}$
-
- Montrer que : $(\forall m, n \in \mathbb{N}): m^{2} \mid n^{2} \Rightarrow m \mid n$.
- Montrer qu’il suffit d’étudier le cas ou $x \wedge y=1$.Dans la suite on suppose que $x \wedge y=1$ dans l’équation $(E)$.
- Montrer que si $(x, y, z)$ est solution de l’équation $(E)$ alors $x$ et $z$ sont impaires et $y$ paire.
- On pose $d=(z-x) \wedge(z+x)$. Montrer que d est paire et en déduire que $d=2$.
- Montrer que si $a^{2}=b c$ et $c \wedge b=1$ alors il existe $b^{\prime}$ et $c^{\prime}$ tels que $b=b^{\prime 2}$ et $c=c^{2}$.
- Soit $\alpha$ et $\beta \in \mathbb{N}$ tels que $3-x=2 \alpha$ et $3-x=2 \alpha$.
Montrer que $\alpha$ ou $\beta$ est paire , en déduire les solutions de l’équation $(E)$.

Pour tout $n \in \mathbb{N}^{*}$ on pose $x_{n}=2^{n}-1$.
Partie I :
-
- Montrer que $\left(\forall n \in \mathbb{N}^{*}\right): x_{n+1}=2 x_{n}+1$
- En déduire que : $\left(\forall n \in \mathbb{N}^{*}\right): x_{n+1} \wedge x_{n}=1$
- Montrer que : $n \equiv 0[6] \Leftrightarrow x_{n} \equiv 0[9]$ (Remarquer que : $2^{6} \equiv 1[9]$)
- En déduire qu’il existe une infinité de nombres $n \in \mathbb{N}^{*}$ tels que $n \wedge x_{n} \neq 1$.
- Montrer que $\left(\forall(n, m) \in \mathbb{N}^{* 2}\right): n \mid m \Rightarrow x_{n} \mid x_{m}$
- Soient $m, n \in \mathbb{N}^{*}$. Montrer que si $r$ est le reste de la division euclidienne de $m$ sur $n$ alors $x_{r}$ est le reste de la division euclidienne de $x_{m}$ sur $x_{n}$. (Remarquer que : $2^{n} \equiv 1\left[x_{n}\right]$).
- En déduire que $x_{m} \wedge x_{n}=x_{n} \wedge x_{r}$.
- Montrer en utilisant l’algorithme d’Euclide que: $\left(\forall(m, n) \in \mathbb{N}^{* 2}\right): x_{m} \wedge x_{n}=x_{m \wedge n}$
Partie II :
Dans la suite en veut monter que $\left(\forall k \in \mathbb{N}^{*}\right)(\exists i \in\{1,2,3, \ldots . ., 2 k\}): 2 k+1 \mid x_{i}$.
On suppose le contraire c.à $d \quad\left(\exists k \in \mathbb{N}^{*}\right)(\forall i \in\{1,2,3, \ldots ., 2 k\}): x_{i} \neq 0[2 k+1]$
Et soit $R_{i}$ le reste de la division euclidienne de $x_{i}$ par $2 k+1$.
- Montrer que : $(\forall i \in\{1,2,3, \ldots \ldots, 2 k\}): 1 \leq R_{i} \leq 2 k$.
- Montrer que : $x_{i} \equiv 2 k[2 k+1] \Leftrightarrow 2^{i} \equiv 0[2 k+1]$
- En déduire que : $(\forall i \in\{1,2,3, \ldots . ., 2 k\}): R_{i} \neq 2 k$.
- Montrer que les restes $R_{i}$ sont distincts deux à deux.
- Conclure.

- Soient $a, b, c, d \in \mathbb{N}^{*}$. Montrer que : \[d = a \wedge b \Rightarrow \left( {\exists \left( {u,v} \right) \in \mathbb{N}} \right):d = au – bv\]
- Soient $m, n, p \in \mathbb{N}^{*}$ tels que $2^{m} \equiv 1[p]$ et $2^{n} \equiv 1[p]$. Montrer que $2^{m \wedge n} \equiv 1[p]$.

- Soient $a, b, c \in \mathbb{Z}$ tel que : $a \wedge b=1$. Trouver un nombre $x$ tel que : $(a+b x) \wedge c=1$
- Résoudre dans $\mathbb{Z}^{2}$ l’équation $(a \wedge b)+(a \vee b)=b+9$
- On suppose ici que a divise $b$. Montrer que $b \wedge c=(a \wedge c)\left[\dfrac{c}{a \wedge c} \wedge \dfrac{b}{a}\right]$ et $(a \vee c) \dfrac{b}{a}=(b \vee c)\left[\dfrac{c}{a \wedge c} \wedge \dfrac{b}{a}\right]$

Dans le système de numération de base $a$, on donne l’écriture des naturels $x, y$ et $z$ : $$x=\overline{111},\,\,\, y=\overline{114} \text{ et } z=\overline{13054}$$
- Écrivez dans ce même système de numération les naturels $x+y$ et $x+z$.
- Déterminez $a$ sachant que $z$ est le produit de $x$ et $y$.

On veut déterminer les chiffres $x, y$ et $z$ pour lesquels $x y z_{12}=x y z 0_{5}$.
- Quelles inégalités larges à propos des entiers $x$, $y$ et $z$ pouvez-vous écrire d’emblée?
- Montrez que l’égalité à obtenir équivaut à $19 x-13 y=4 z$.
- Grâce à l’algorithme d’Euclide, déterminez des naturels $X$ et $Y$ tels que $19 X-13 Y=1$.
- Prouvez que si des entiers $x$, $y$ et $z$ vérifient $19 x-13 y=4 z$, il existe un entier $k$ tel que : $x=-8 z+13k$ et $y=-12 z+19 k$.
- Montrez que dans les égalités du $4)$, on ne peut pas avoir $k \leq 0$.
- Quelle est la plus grande valeur possible pour $x+8z$? En déduire qu’on a nécessairement $k \leq 2$.
- Montrez que dans la division euclidienne de $19k$ par 12, $y$ est le reste et $z$ est le quotient.
- Concluez.

Soit $z \in \mathbb{C}$ tel que $|z|=1$ et $z^{2} \neq 1$. Montrer que le nombre $\dfrac{z^{2}+1}{z^{2}-1}$ est imaginaire pure.

Soit $z \in \mathbb{C}-\{-i\}.$ Montrer que : $\operatorname{Im}(z) > 0 \Leftrightarrow\left|\dfrac{z-i}{z+i}\right|<1$

Soient $a$, $b$ et $c$ trois nombres complexes tels que : $|a|=|b|=|c|=1.$
- Montrer que : $\left|\dfrac{a-b}{1-a \bar{b}}\right|=1.$
- Montrer que : $\left|a b+b c+c a\right|=\left|a+b+c\right|.$

- Montrer que : $$(\forall z \in \mathbb{C}),\,\,|z+1|=|z|+1 \Leftrightarrow z \in \mathbb{R}^{+}.$$
- Montrer que : $\left(\forall\left(z, z^{\prime}\right) \in \mathbb{C}^{2}\right),$ $$\left|z+z^{\prime}\right|=|z|+z^{\prime} \mid \Leftrightarrow\left(\exists \alpha \in \mathbb{R}^{+}\right):\left(z=\alpha z^{\prime}\right. \text{ ou } \left. z^{\prime}=\alpha_{z}\right)$$

Pour tout $z \neq 1$ on pose $z^{\prime}=\dfrac{z-1}{1-\bar{z}}$ et on considère les points $M(z)$ et $M^{\prime}\left(z^{\prime}\right).$
- Montrer que $\left|z^{\prime}\right|=1$, $\dfrac{z^{\prime}-1}{z-1}$ est réel et $\dfrac{z^{\prime}+1}{z-1}$ est imaginaire pure.
- En déduire une construction géométrique du pont $M^\prime$ à partir du point $M.$

Pour tout $z \neq i$ on pose $f(z)=\dfrac{\bar{z}}{1-i \bar{z}}$
- Montrer que : $$f(z) \in \mathbb{R} \Leftrightarrow|z|^{2}-\operatorname{Im}(z)=0.$$
- Déterminer la nature des deux ensembles : $E=\{M(z) \in P / f(z) \in \mathbb{R}\}$ et $F=\{M(z) \in P / f(z) \in i\mathbb{R}\}$
- On considère les points $A(i), M(z), M^{\prime}(f(z))$
- Montrer que : $f(z)-i=\dfrac{-i}{1-i \bar{z}}.$ En déduire l’ensemble $G=\{M(z) \in P /|f(z)-i|=2\}$
- Montrer que $f(z)-i=\dfrac{1}{|1-i \bar{z}|^{2}}(z-i).$ En déduire un mesure de l’angle $\left( {\widehat {\overrightarrow {AM} ,\overrightarrow {AM’} }} \right)$

Soit $A$, $B$ et $C$ trois points distincts du plan complexe d’affixes $a$, $b$ et $c$.
Montrer que les trois propositions suivantes sont équivalentes :
- ABC est un triangle équilatéral.
- $j$ ou $j^{2}$ est solution de l’équation $a z^{2}+b z+c=0$.
- $a^{2}+b^{2}+c^{2}=ab+bc+ca$
Application : Soit $ABC$ un triangle du plan affine euclidien. On construit, à l’extérieur de ce triangle, les trois triangles équilatéraux de bases $A B$, $B C$, $C A$. Montrer que les centres de gravité de ces trois triangles forment un triangle équilatéral.

- Soit $(\mathscr{C})$ le cercle de centre $A\left(z_{0}\right)$ et de rayon $R$. Montrer que $(\mathcal{C})$ est l’ensemble des points $M\left(z_{0}\right)$ tels que: $z \bar{z}-\bar{z}_{0} z-z_{0} \bar{z}+z_{0} \bar{z}_{0}-R^{2}=0$
- Réciproquement, soient $c \in \mathbb{C}$ et $\gamma \in \mathbb{R}$. Quel est l’ensemble des points $M(z)$ tels que $z \bar{z}-\bar{cz}-c \bar{z}+\gamma=0.$
- Application : Soient $\theta \in\mathbb{R}$ et $(a, b) \in \mathbb{C}^{2}$ avec $a \neq b$. On considère les points $A(a)$ et $B(b).$
Trouver l’ensemble des points $M$ tels que $(\overline{\overrightarrow{M A}, \overrightarrow{M B}}) \equiv \theta[\pi]$

Soient $u, v, w$ trois nombres complexes unitaires tels que $u+v+w=0$.
- Montrer que $\operatorname{Re}(v \bar{w})=\dfrac{-1}{2}$. En déduire la valeur de $v \bar{w}$.
- Montrer que : $u=j v=j^{2} w$ ou $u=j w=j^{2} v$.

On pose $u=e^{\frac{2 i \pi}{7}},$ $S=u+u^{2}+u^{4}$ et $T=u^{3}+u^{5}+u^{6}$
- Montrer que $S$ et $T$ sont conjugués et $\operatorname{Im}(S)>0$.
- Calculer : $S+T$ et $S T$. En déduire $S$ et $T.$
- Calculer : $\dfrac{u}{1+u^{2}}+\dfrac{u^{2}}{1+u^{4}}+\dfrac{u^{3}}{1+u^{6}}$
- En déduire la valeur de : $\dfrac{1}{\cos \dfrac{2 \pi}{7}}+\dfrac{1}{\cos \dfrac{4 \pi}{7}}+\dfrac{1}{\cos \dfrac{6 \pi}{7}}.$

- Résoudre dans $\mathbb{C}$ l’équation $z^{2}+z+1=0$
- Pour tout $z=e^{i \theta}$ avec $-\pi \leq \theta \leq \pi$ et $\theta \neq \dfrac{2 \pi}{3}$ et $\theta \neq-\dfrac{2 \pi}{3}$, on pose $z^{\prime}=\dfrac{1}{z^{2}+z+1}$.
- Montrer que : $z^{2}+z+1=z(1+z+\bar{z}).$
- Calculer le module et l’argument $z^\prime$ en fonction de $\theta$.
- On pose $z^{\prime}=x+iy$ avec $x$ et $y$ deux nombres réels. Montrer que : $x^{2}+y^{2}=(1-2 x)^{2}.$
- En déduire que le point $M$ d’affixe $z^\prime$ appartient à une hyperbole dont on déterminera le centre les sommets et les asymptotes.

Soit $a$ un nombre complexe dont la forme algébrique est $a=\alpha+i \beta$.
- Déterminer la nature de $(H)=\left\{M(z) / z^{2}-(\bar{z})^{2}=a^{2}-(\bar{a})^{2}\right\}$ et tracer $(H)$ pour $a=1+i.$
- Déterminer la nature de $(C)=\{M(z) /(z-a)(\bar{z}-\bar{a})=4 a \bar{a}\}$ et tracer $(C)$ pour $a=1+i.$
- On considère dans $\mathbb{C}$ le système $(S):\left\{\begin{array}{l}z^{2}-(\bar{z})^{2}=a^{2}-(\bar{a})^{2} \\ (z-a)(\bar{z}-\bar{a})=4 a \bar{a}\end{array}\right.$ et on pose $u=z-a.$
- Montrer que le système est équivalent au système $(S^\prime) :\left\{\begin{array}{l}u \bar{u}=4 a \bar{a} \\ (u+2 a)\left(u^{3}-8 a(\bar{a})^{2}\right)=0\end{array}\right.$
- On pose $a=r e^{i \theta}$ avec $r>0$ et $-\pi<\theta \leq \pi$. Déterminer en fonction de $r$ et $\theta$ les affixes des point d’intersection de $(C)$ et $(H)$.
- Montrer que l’intersection de $(C)$ et $(H)$ contient trois points sommets d’un triangle équilatéral.

Résoudre dans $\mathbb{C}$ l’équation $\left(z^{2}+1\right)^{n}+(z-i)^{2 n}=0$

Soit $(a, b) \in \mathbb{R}^{2}$ avec $a \neq b.$
- Résoudre dans $\mathbb{C}$ l’équation $(z-b)^{n}-(z-a)^{n}=0.$
- Prouver que les solutions sont affixes de points alignés.
- On considère le nombre complexe $a=e^{\frac{2 i \pi}{5}}$. On note $I, A, B, C, D$ les points du plan complexe d’affixes $1, a, a^{2}, a^{3}, a^{4}$.
- Vérifier que $a^{5}=1$ et montrer que $I A=A B=B C=C D=D I$.
- Placer les points $I, A, B, C, D$ dans le plan complexe (unité: $4cm$).
- Vérifier que, pour tout nombre complexe $z$ : $$z^{5}-1=(z-1)\left(1+z+z^{2}+z^{3}+z^{4}\right)$$
- En déduire que : \begin{align}1+a+a^{2}+a^{3}+a^{4}=0\end{align}
- Montrer que $a^{3}=\overline{a}^{2}$ et que $a^{4}=\overline{a}$ et en déduire que: $$(a+\overline{a})^{2}+(a+\overline{a})-1=0 \quad(2)$$
- Résoudre l’équation: $4 x^{2}+2 x-1=0$ et en déduire, à partir de $(2)$, la valeur exacte de $\cos \left(\dfrac{2 \pi}{5}\right)$.

- Montrer que $(\forall z \in \mathbb{C}-\{-1\}):$ $$|z|=1 \Leftrightarrow(\exists \alpha \in \mathbb{R}),\,\,\, z=\frac{1+i \alpha}{1-i \alpha}$$
- Soit $a \in \mathbb{C}, n \in \mathbb{N}^{*}$, montrer qu’une condition nécessaire et suffisante pour que l’équation $\left(\dfrac{1+i x}{1-i x}\right)^{n}=a$ ait des solutions réelles est que $|a|=1.$

Soit $a, b, c \in \mathbb{C}$ tel que $|a|=|b|=|c|=1$ et $a \neq c$ et $b \neq c$.
Montrer que : $$\,\arg \left(\frac{c-b}{c-a}\right) \equiv \frac{1}{2} \arg \left(\frac{b}{a}\right)[2 \pi]$$

Soit $n \in \mathbb{N}^{*}$. Pour chaque $k \in\{0,1,2, \ldots \ldots, 2 n-1\},$ on pose $z_{k}=e^{i \frac{k \pi}{n}}$
- Montrer que : $(\forall k \in\{0,1,2, \ldots ., 2 n-1\}),\,\,\, \overline{z}_{k}=z_{2 n-k}$
- En déduire que le nombre $u=\displaystyle\sum_{k=1}^{n-1} z_{k}$ est imaginaire pur.

On considère le système $$(S) : \left\{\begin{array}{l}z^{5}(1-\bar{z})=1 \\ |z|=|z-1|\end{array}\right.$$
- Montrer que si $z$ est une solution de $(S)$ alors $|z|=|z-1|=1.$
- En déduire que $z$ est une solution de $(S)$ alors $z=e^{i \frac{\pi}{3}}$ ou $z=e^{-i \frac{\pi}{3}}.$
- Résoudre dans $\mathbb{C}$ le système $(S).$

Montrer que $(\forall n \in \mathbb{N}):$ $$(1+i \sqrt{3})^{n}+(1-i \sqrt{3})^{n}=2^{n+1} \cos \left(n \frac{\pi}{3}\right)$$

Soit $p$ un nombre complexes de module $1$ on considère l’équation $\left(E_{p}\right): z^{2}-2 p^{2} z-1=0.$
- Déterminer le nombre complexe $p$ pour que $(E_{p})$ admette une racine double
- Soit $z_{1}$ et $z_{2}$ les racines de $\left(E_{p}\right)$. On pose $u_{1}=\dfrac{1+z_{1}}{p}$ et $u_{2}=\dfrac{1+z_{2}}{p}$
- Calculer $u_{1}+u_{2}$ et $u_{1}u_{2}.$
- Montrer que si $u_{1}$ et $u_{2}$ ne sont pas des réels alors $\left|1+z_{1}\right|=\left|1+z_{2}\right|.$
- Montrer que si $u_{1}$ et $u_{2}$ sont des réels alors $\arg \left(1+z_{1}\right) \equiv \arg \left(1+z_{2}\right)[2 \pi].$

On appelle birapport des quatre complexes $z_{1}, z_{2}, z_{3}, z_{4}$ rangés dans cet ordre le nombre complexe que l’on note $\beta\left(z_{1}, z_{2}, z_{3}, z_{4}\right)$ et défini par $\beta\left(z_{1}, z_{2}, z_{3}, z_{4}\right)=\dfrac{z_{3}-z_{1}}{z_{3}-z_{2}} \div \dfrac{z_{4}-z_{1}}{z_{4}-z_{2}}.$ Soient $M_{1}, M_{2}, M_{3}, M_{4}$ les points d’affixes $z_{1}, z_{2}, z_{3}, z_{4}$. Déterminer une condition nécessaires et suffisante portant sur $\beta\left(z_{1}, z_{2}, z_{3}, z_{4}\right)$ pour que ces points soient cocycliques ou alignés

Déterminer l’ensemble des points d’affixe $z$ tels que :
- Les points d’affixe $1, z, \dfrac{1}{z}, 1-z$ soient cocycliques.
- Les points d’affixe $z, z^{2}, z^{5}$ soient alignés.
- Les points d’affixe $1, z, z^{3}$ soient alignés.
- Les points d’affixe $z, 2 z+1, z-1$ forment un triangle isocèle en $M$.
- Les points d’affixe $1,1+z, 1+z^{2}$ forment un triangle équilateral.

- Résoudre dans l’équation $(1+i z)^{5}=(1-i z)^{5}.$
- En déduire $\tan \dfrac{\pi}{5}$ et $\tan \dfrac{2 \pi}{5},$ et les exprimer sous la forme $\sqrt{p + q \sqrt{n}},$ où $n, p$ et $q$ sont des éléments de $\mathbb{Z}.$
- Calculer $\tan \left(\dfrac{\pi}{60}\right).$

On pose $u=e^{\frac{2 i \pi}{5}}$
- Montrer que $1+u+u^{2}+u^{3}+u^{4}=0$ et exprimer $\cos \left(\dfrac{2 \pi}{5}\right)$ en fonction des puissances de $u$.
- En déduire que $\cos \left(\dfrac{2 \pi}{5}\right)$ est racine de l’équation $4 x^{2}+2 x-1=0.$
- Calculer $\cos \left(\frac{2 \pi}{5}\right)$, $\cos \left(\dfrac{4 \pi}{5}\right), \cos \left(\dfrac{6 \pi}{5}\right), \cos \left(\dfrac{8 \pi}{5}\right)$ puis $\cos \left(\dfrac{\pi}{5}\right)$.

En utilisant la formule de Newton déduire les valeurs des sommes : $$
A=\sum_{k=0}^{n} C_{n}^{k} \cos \left(\frac{2 k \pi}{n}\right) \quad \text { et } \quad B=\sum_{k=0}^{n} C_{n}^{k} \sin \left(\frac{2 k \pi}{n}\right)$$

Soit $n \in \mathbb{N}^{*}$ et $\omega=e^{i \frac{2 \pi}{n}}$ pour tout $k \in\{0,1,2, \ldots . ., n-1\}$ on note $A_{k}$ le point d’affixe $\omega^{k}.$
- Montrer que $A_{k+1}$ est l’image de $A_{k}$ par la rotation $r$ de centre $O$ et d’angle $\dfrac{2 \pi}{n}$.
- Calculer la somme $S=\displaystyle\sum_{k=0}^{n-1} A_{k} A_{k+1}.$

Soit $\alpha \in \mathbb{R}$ et $m \in \mathbb{C}$. On considère l’équation $(E): z^{2}-m z+e^{i \alpha}=0$ on désigne par $z_{0}$ et $z_{1}$ les solutions de l’équation $(E)$.
- Montrer que $\arg \left(z_{0}\right) \operatorname{targ}\left(z_{1}\right) \equiv 0[2 \pi]$ et $\left|z_{0}\right|\left|z_{1}\right|=1.$
- On suppose que $z_{0}=e^{i \theta}$. Donner la forme exponentielle de $m.$

Soit $\alpha \in\left]-\dfrac{\pi}{2}, \dfrac{\pi}{2}\right[.$ On considère l’équation $\left(E_{\alpha}\right): z^{2}-2 z+1+\tan ^{2}(\alpha)=0.$
- Résoudre dans $\mathbb{C}$ l’équation $\left(E_{\alpha}\right)$ on notera $z_{1}, z_{2}$ ses solutions.
- Déterminer la forme trigonométrique de $z_{1}$ et $z_{2}$.
- Soient $M_{1}$ et $M_{2}$ les points images de $z_{1}$ et $z_{2}$ respectivement.
- Montrer que $OM_{1}=OM_{2}$.
- Déterminer la valeur de $\theta$ pour que le triangle $\left(O M_{1} M_{2}\right)$ soit équilatère directe.

Soit $\left(u_{n}\right)$ la suite définie par $\left\{\begin{array}{l}u_{0}=2 \\ u_{n+1}=u_{n}+\arccos \left(\dfrac{1}{u_{n}}\right)\end{array}\right.$
- Montrer que $(\forall n \in \mathbb{N}):\,\, u_{n}>1.$
- Etudier le sens de variation de $\left(u_{n}\right).$
- Montrer que $(\forall n \in \mathbb{N}):\,\, u_{n}>n \dfrac{\pi}{3}+2$.
- En déduire que la suite $\left(u_{n}\right)$ n’est pas majorée.

Soit $\left(u_{n}\right)_{n \geqslant 1}$ la suite définie par : $\displaystyle u_{n}=\prod_{k=1}^{n} \cos \left(\dfrac{\alpha}{2^{k}}\right)$
- Montrer que la suite $\left(u_{n}\right)$ est décroissante et minorée et déduire qu’elle est convergente.
- Montrer que $(\forall n \geq 1):\,\, u_{n}=\dfrac{\sin (\alpha)}{2^{n} \sin \left(\dfrac{\alpha}{2^{n}}\right)}$ et en déduire la limite de la suite $\left(u_{n}\right).$

Soit $\left(u_{n}\right)_{n \geqslant 1}$ la suite définie par : $\displaystyle\left\{\begin{array}{l}u_{1}=1 \\ u_{n+1}=\dfrac{n+u_{n}}{n^{2}}\end{array}\right.$
- Montrer que $(\forall n \geq 1): u_{n} \leq 2$. En déduire que $\left(u_{n}\right)$ est convergente et calculer sa limite $\ell.$
- Montrer que $(\forall n \geq 2): \dfrac{1}{n-1} \leq u_{n} \leq \dfrac{n+1}{(n-1)^{2}}$. En déduire $\lim \left(n u_{n}\right).$
- On veut étudier la monotonie de la suite $\left(u_{n}\right)$.
- Montrer que la suite $\left(v_{n}\right)_{n \geq 2}$ définie par $v_{n}=\dfrac{n}{n^{2}-1}$ est décroissante.
- Montrer que pour tout $n \geq 2$, on a $u_{n} \geq v_{n}$.
- En déduire que la suite $\left(u_{n}\right)_{n \geqslant 2}$ est décroissante .

Soit $\left(u_{n}\right)_{n \geqslant 1}$ la suite définie par $\displaystyle\left\{\begin{array}{l}u_{1}=2 \\ u_{n+1}=\dfrac{(n+2) u_{n}+2\left(n^{2}+n-1\right)}{(n+1)^{2}}\end{array}\right.$
- Montrer que la suite $\left(u_{n}\right)$ est décroissante.
- Montrer que $\left(u_{n}\right)$ est convergente et calculer sa limite $\ell.$
- Calculer $u_{n+1}-\ell$ en fonction de $u_{n}-\ell$. En déduire $u_{n}$ en fonction de $n.$

Soit $\left(u_{n}\right)$ la suite définie par $\left\{\begin{array}{l}u_{0}=2 \\ u_{n+1}=2 \sqrt[3]{u_{n}}+\dfrac{1}{n+1}\end{array}\right.$
- Montrer que $(\forall n \in \mathbb{N}): u_{n}>1.$
- Etudier le sens de variation de $\left(u_{n}\right).$
- Montrer que $\left(\mathrm{u}_{\mathrm{n}}\right)$ est convergente et donner sa limite.

Soit $\theta \in\left] 0, \dfrac{\pi}{2}\right[$, pour tout $n \in \mathbb{N}$ on pose $u_{n}=2^{n} \sin \left(\dfrac{\theta}{2^{n}}\right)$ et $v_{n}=2^{n} \tan \left(\dfrac{\theta}{2^{n}}\right).$
Montrer que les suites $\left(u_{n}\right)$ et $\left(v_{n}\right)$ sont adjacentes et déterminer leur limite commune.

Soient $a$ et $b$ deux nombres réels tels que $0 < a < b$. On considère les deux suites $\left(a_{n}\right)_{n \ge 0}$ et $\left(b_{n}\right)_{n \ge 0}$ définies par :
$$\left\{\begin{aligned}& a_{0}=a,\,\,\, b_{0}=b\\ & a_{n+1}=\frac{1}{2}\left(a_{n}+b_{n}\right)\end{aligned}\right.\,\,\,\text { et }\,\,\, b_{n+1}=\sqrt{\frac{1}{2}\left(a_{n}^{2}+b_{n}^{2}\right)}$$
- Montrer que les suites $\left(a_{n}\right)_{n \ge 0}$ et $\left(b_{n}\right)_{n \ge 0}$ sont convergentes et ont la même limite.
- Montrer que pour tout $n \geq 0 :$ $$0 \leq b_{n+1}-a_{n+1} \leq \dfrac{1}{8 a}\left(b_{n}-a_{n}\right)^{2}.$$
- En déduire que pour tout $n \geq 0:$ $$0 \leq b_{n}-a_{n} \leq 8 a\left(\dfrac{b-a}{8 a}\right)^{2^{n}}.$$

Soit $\left(u_{n}\right)_{n \geqslant 1}$ la suite définie par : $$\left\{\begin{array}{l}u_{0}=1 \\ u_{n+1}=u_{n}+\dfrac{1}{u_{n}}\end{array}\right.$$
- Montrer que $(\forall n \geq 0): u_{n} \geq 1.$
- Etudier les variations de la suite $\left(u_{n}\right).$
- Montrer que $(\forall n \geq 1)$ : $2 \leq u_{n}^{2}-u_{n-1}^{2} \leq 2+u_{n}-u_{n-1}$ et $2 n \leq u_{n}^{2}-1 \leq 2 n+u_{n}-1.$
- En déduire la divergence de la suite $\left(u_{n}\right).$
en déduire que $\left(u_{n}\right)$ est convergente et calculer sa limite $l.$ - Montrer que $(\forall n \geq 0): 1-\dfrac{1}{u_{n}} \leq \dfrac{2 n}{u_{n}^{2}} \leq 1-\dfrac{1}{u_{n}^{2}}$. En déduire $\lim \left(\dfrac{1}{\sqrt{2 n}} u_{n}\right).$

Soit $n \in \mathbb{N}^{*}$. On considère la fonction définie sur $\mathbb{R}^{+}$par : $f_{n}(x)=3 x^{n}-x-1$
- Montrer que $f_{n}$ est croissante sur $\left[\sqrt[n-1]{\dfrac{1}{3 n}},+\infty\right[$ et décroissante sur $\left[0, \sqrt[n-1]{\dfrac{1}{3 n}}\right],$ puis poser le tableau de variation de $f_{n}$.
- Montrer que l’équation $f_{n}(x)=0$ admet une solution unique $u_{n}$ dans l’intervalle $[0,+\infty[$.
- Calculer $f_{n}(1)$, en déduire que $\left(\forall n \in \mathbb{N}^{*}\right):\,\,$ $0 < u_{n} < 1$.
- Montrer que : $(\forall x \in] 0,1[):\,\, f_{n+1}(x) < f_{n}(x)$
- Montrer que $\left(u_{n}\right)$ est croissante, en déduire qu’elle est convergente.
- On pose $\lim u_{n}=\ell$
- Montrer que: $0 \leq \ell \leq 1$
- Montrer que: $\left(\forall n \in \mathbb{N}^{*}\right): u_{n} \leq l$ (penser au raisonnement par absurde)
- Montrer que : $\ell=1.$ (penser au raisonnement par absurde encore)

On considère la suite $\left(u_{n}\right)_{n \in \mathbb{N}}$ définie par : $\left\{
\begin{array}{l}
u_{0} \in\ \left]0,1\right[\\
u_{n+1}=u_{n}-u_{n}^{2}
\end{array}\right.$
Et on pose $v_{n}=n u_{n}$
-
- Montrer que $(\forall n \in \mathbb{N}):\,\, 0 < u_{n} < \dfrac{1}{n+1}$.
- Montrer que la suite $\left(v_{n}\right)$ est croissante.
- Montrer que la suite $\left(v_{n}\right)$ converge vers un réel $\lambda$ tel que $0<\lambda \leq 1$
- Montrer que la suite $w_{n}=n\left(v_{n+1}-v_{n}\right)$ converge vers une limite $\ell$ à déterminer.
- Montrer que si $\lambda \neq 1$ alors : $$\left(\exists n_{0} \in \mathbb{N}^{*}\right)(\exists a>0): n>n_{0} \Rightarrow v_{n+1}-v_{n}>\frac{a}{n}$$
- En déduire que $\left(\forall n>n_{0}\right): v_{2 n} \rightarrow v_{n}>\dfrac{a}{2}$.
- Montrer que $\lim v_{n}=+\infty$.
- Déterminer $\lim v_{n}$.

Soit $a \in[0,1]$, et soit $\left(u_{n}\right)_{n \geqslant 1}$ la suite définie par $\left\{\begin{array}{l}u_{0}=0 \\ u_{n+1}=u_{n}+\dfrac{1}{2}\left(a^{2}-u_{n}^{2}\right)\end{array}\right.$
- Soient $x_{n}=a-u_{n}$ et $y_{n}=a+u_{n}$. Trouver des relations liant $x_{n+1}$ et $y_{n+1}$ à $x_{n}$ et $y_{n}.$
- Montrer que $(\forall n \in \mathbb{N}): x_{n} \geq 0$ et $y_{n} \geq 0$. En déduire la monotonie de la suite $\left(u_{n}\right)$.
- Montrer que la suite $\left(u_{n}\right)$ est convergente et déterminer sa limite.

Pour tout $n \in \mathbb{N}^{*}$ on définie la fonction $f_{n}$ sur $\mathbb{R}$ par : $f_{n}(x)=\displaystyle\sum_{k=1}^{n} k x^{k}$.
- Simplifier l’expression $(1-x)^{2} f_{n}(x)$. En déduire une autre expression de $f_{n}(x)$ pour $x \neq 1$.
- Pour tout $x \in[0,1]$, On pose $F(x)=\displaystyle\lim _{n \rightarrow+\infty} f_{n}(x).$
- Donner l’expression de $F(x)$.
- Représenter sur un même graphique, dans l’intervalle $[0,1]$, les fonctions $f_{1}, f_{2}, f_{3}$ et $F$.
- Montrer que, pour tout $n \in \mathbb{N}^{*}$, l’équation $f_{n}(x)=1$ admet une unique solution, notée $u_{n}$, dans l’intervalle $[0,1]$. Puis calculer $u_{1}$ et $u_{2}.$
- Etudier le sens de variation de le suite $\left(u_{n}\right)$. En déduire qu’elle converge. On notera $\ell$ sa limite.
- Montrer que $\left(\forall x \in\left[0, \dfrac{1}{2}\right]\right)\left(\forall n \in \mathbb{N}^{*}\right):\left| F(x)-f_{n}(x)\right| \leq 6 \dfrac{n+1}{2^{n+1}}$.
- Montrer que $\displaystyle\lim _{n \rightarrow+\infty} f_{n}\left(u_{n}\right)=F(\ell)$. En déduire la valeur de $\ell.$

Pour tout $n \in \mathbb{N}$ on définie la fonction $f_{n}$ sur $\mathbb{R}$ par: $f_{n}(x)=x^{n+1}+x^{n}+\cdots+x-1.$
- Montrer que l’équation $f_{n}(x)=0$ admet une seule solution dans $[0,1]$, notée $u_{n}$.
- Montrer que $(\forall n \in \mathbb{N}): f_{n}\left(u_{n+1}\right)<0$. En déduire le sens de variation de $\left(u_{n}\right)$.
- Calculer la limite de $\left(u_{n}\right)$.
- Soit $a_{n}=u_{n}-\dfrac{1}{2}$. Montrer que $\lim (n+1) a_{n}=0$. En déduire $\lim 2^{n+2}\left(u_{n}-\dfrac{1}{2}\right).$

On considère la fonction f définie par $\left\{\begin{align*}&f(x)=x \sin \left(\frac{1}{x}\right) &;&\,\, x>0 \\ &f(0)=1 & &\\ &f(x)=x E\left(\frac{1}{x}\right) &;&\,\, x<0\end{align*}\right.$
- Etudier la continuité de la fonction $f$ en $0$.
- Calculer $\displaystyle\lim _{|x| \rightarrow+\infty} f(x).$

&\textbf{1.}\quad f(x)=E(x)(x-E(x))
&\textbf{2.}&\quad f(x)=\left|x-2 E\left(\frac{x+1}{2}\right)\right|\\
&\textbf{3.}\quad f(x)= \begin{cases}0 & \text { si } x \in \mathbb{Z}\\ x & \text { si } x \notin \mathbb{Z}\end{cases}
&\textbf{4.}&\quad f(x)= \begin{cases}0 & \text { si } x \in \mathbb{Q} \\ x & \text { si } x \notin \mathbb{Q}\end{cases}\end{align}$$

Soit $f$ une fonction continue sur un segment $[a, b]$.
Montrer qu’il existe $c \in[a, b]$ tel que $2 f(a)+3 f(b)=5 f(c).$

Soient $f$ et $g$ et $h$ trois fonctions continues sur un intervalle $I$ telles que:
$$(\forall x \in I):\,\, g(x) \leq f(x) \leq h(x)$$Montrer que si chacune des deux fonctions $g$ et $h$ admet un point fixe dans $I$ alors $f$ en admet un aussi.

Soit $f, \mathbb{R} \rightarrow \mathbb{R}$ continue telle que $\displaystyle\lim _{x \rightarrow-\infty} f(x)=-\infty$ et $\displaystyle\lim _{x \rightarrow+\infty} f(x)=+\infty$
Montrer que $f$ s’annule. Appliquer ceci aux polynôme de degré impair.

Soit $f$ une fonction continue sur $[0,1]$ telle que $f(0)=f(1)=0,\, (\forall x \in[0,1]):\,\, f(x) \geq 0.$
Montrer que : $\quad(\forall \lambda \in] 0,1[)\left(\exists x_{\lambda} \in[0,1]\right): f\left(x_{\lambda}+\lambda\right)=f\left(x_{\lambda}\right)$.

Soient $f, g:[a, b] \rightarrow \mathbb{R}$ continues. On suppose que $(\forall x \in[a, b]): f(x)>g(x)>0$
Montrer qu’il existe $k>1$ tel que $f>k g.$

Soient $f, g:[a, b] \rightarrow \mathbb{R}$ continues. On suppose que $(\forall x \in[a, b])(\exists y \in[a, b])$ tel que $f(x)=g(y)$.
Montrer qu’il existe $x \in[a, b]$ tel que $f(x)=g(x)$.

Montrer que toute fonction polynôme de $\mathbb{R}$ dans $\mathbb{R}$ de degré impaire, s’annule en au moins un point.

Soit $f$ une fonction continue sur un segment $[a, b]$ et $[m, M]$ un segment contenant $f(a)$ et $f(b)$.
Montrer que la courbe représentative de $f$ coupe les diagonales du rectangle $[a, b] \times[m, M].$

- Montrer que : $\left(\forall n \in \mathbb{N}^{*}\right)\left(\exists!a_{n} \in\right] 0,1[),\,\,\,\, 2 n a_{n} \tan \left(\dfrac{\pi}{2} a_{n}\right)=\pi$
- Comparer $a_{n}$ et $a_{n+1}.$
- Montrer que $a_{n}$ est solution de l’équation $2\arctan \left( {\dfrac{\pi }{{2nx}}} \right) – \pi x = 0.$

On considère la fonction $f(x)=\dfrac{4 x}{x^{2}+1}$. Montrer que $f$ est une bijection de $[-1,1]$ vers un intervalle à déterminer puis déterminer $f^{-1}(x).$

Soit $f$ une fonction définie de $\mathbb{R}$ dans $\mathbb{R}$ tel que:$$
f \text { continue en } 0 \quad \text { et } \quad\left(\forall(x, y) \in \mathbb{R}^{2}\right): f(x+y)=f(x)+f(y)$$
- Montrer que $f(0)=0$.
- Montrer que : $\left(\forall(x, y) \in I R^{2}\right): f(x)=f(x-y)+f(y)$.
- En déduire que $f$ est continue sur $\mathbb{R}$.

Soit $f$ une fonction définie sur $] 0,+\infty[$. On suppose que $f$ est croissante sur $] 0,+\infty[$ et la fonction $g$ définie par $g(x)=\dfrac{f(x)}{x}$ est décroissante sur $] 0,+\infty[$.
- Soit $\left.x_{0} \in\right] 0,+\infty\left[\right.$. Montrer que : $$\left(\forall x>x_{0}\right): 0 \leq f(x)-f\left(x_{0}\right) \leq\left(x-x_{0}\right) g\left(x_{0}\right)$$ et
\[\left( {\forall x < {x_0}} \right):\left( {x -{x_0}} \right)g\left( {{x_0}} \right) \le f(x) -f\left( {{x_0}} \right) \le 0\] - Montrer que $f$ est continue sur $] 0,+\infty[$.

Soit $f$ une fonction continue sur $ \left] {a,b} \right[$ tel que : $\left\{\begin{align*}&\lim _{x \rightarrow a^{+}} f(x)=+\infty \\ &\lim _{x \rightarrow b^{-}} f(x)=-\infty\end{align*}\right.$
- Montrer que : $\exists(\alpha, \beta) \in\left] a, b\right[^{2}/\,\,\, f(\alpha) \cdot f(\beta)<0.$
- En déduire que l’équation $f(x)=0$ admet au moins une solution dans l’intervalle $] a, b[$.
- Soit $g$ une fonction continue sur $[a, b]$. Montrer que: $\exists c \in] a, b[/\,\,\, f(c)=g(c)$
- Montrer que : \[\exists c \in \left] {a,b} \right[/\,\,\,\sqrt {\frac{{b -c}}{{c -a}}} – \sqrt {\frac{{c -a}}{{b -c}}} = \sqrt {\left( {b -c} \right)\left( {c -a} \right)} \]

On considère la fonction $f(x)=(\sqrt[3]{1-x}-1)^{3}+1$.
Montrer que $f$ est une bijection de $]-\infty, 1]$ vers un intervalle à déterminer puis déterminer $f^{-1}(x)$.

On considère la fonction $f(x)=\left(\sqrt{\dfrac{1}{2}-\dfrac{1}{\pi} \arcsin x}-1\right)^{3}$.
- Déterminer le domaine de définition de $f$.
- Montrer que $f$ est une bijection de $[-1,1]$ vers un intervalle à déterminer puis déterminer $f^{-1}(x)$.

On considère la fonction $f$ définie par $f(x)=\dfrac{1+\cos x}{\sin x}.$
- Déterminer le domaine de définition de $f$. est ce que $f$ réalise une bijection de $D_{f}$ vers $\mathbb{R}$?
- Soit $g$ la restriction de $f$ à $I=\left] 0, \dfrac{\pi}{2}\right]$.
- Montrer que $g$ est une bijection de $I$ vers un intervalle $J$ à déterminer.
- Déterminer $g^{-1}(x)$.
- En déduire que : $(\forall x \in J): \arcsin\left(\dfrac{2 x}{1+x^{2}}\right)=\arccos\left(\dfrac{x^{2}-1}{x^{2}+1}\right)$

Pour tout entier $n$ non nul on considère la fonction $f_{n}$ définie sur $\mathbb{R}^{+}$ par : $f_{n}(x)=\displaystyle\sum_{k=1}^{n} k x^{k}.$
- Montrer que pour tout $n \geq 1$ l’équation $f_{n}(x)=1$ admet un unique solution positive que l’on notera $u_{n}$
- Comparer $u_{n}$ et $u_{n+1}.$

On considère la fonction $f$ définie par : $f(x)=\arcsin \left(\dfrac{2 x}{1+x^{2}}\right).$
- Déterminer $D_{f}$.
- Montrer que : $f(x)=\left\{\begin{array}{ccc}-\pi-2 \arctan x & ; & x \leq-1 \\ 2 \arctan x & ; & -1 \leq x \leq 1 \\ \pi-2 \arctan x & ; & x \geq 1\end{array}\right.$
- Soit $g$ la restriction de $f$ à $I=[1,+\infty[$.
Montrer que $g$ est une bijection de $I$ vers un intervalle $J$ à déterminer puis déterminer $g^{-1}(x)$.

On considère la fonction $f$ définie par : $$\left\{\begin{array}{l}f(x)=\arcsin (2 x-1)+\arctan \sqrt{\dfrac{1-x}{x}} ; x \in\left] 0,1\right] \\ f(0)=0\end{array}\right.$$
- Montrer que : $(\forall x \in] 0,1])\left(\exists \alpha \in\left[0, \dfrac{\pi}{2}\right[\right):\quad x=\cos ^{2} \alpha.$
- En déduire que $(\forall x \in[0,1]):\quad f(x)=\dfrac{\pi}{2}-\arccos \sqrt{x}.$
- Que $f$ est une bijection de $[0,1]$ vers un intervalle $J$ à déterminer puis déterminer $f^{-1}(x)$.

On considère la fonction $f$ définie par : $$f(x)=\arctan\left(\dfrac{x-\sqrt{1-x^{2}}}{x+\sqrt{1-x^{2}}}\right)$$
- Déterminer $D_{f}$.
- Montrer que : \[
\left\{
\begin{aligned}
&f(x)=\arcsin x+\dfrac{3\pi}{4} &si & & -1\le x\le \dfrac{-\sqrt{2}}{2}\\
& f(x)=\arcsin x-\dfrac{\pi}{4} &si & & -\dfrac{\sqrt{2}}{2}\le x\le 1
\end{aligned}
\right.
\]

On considère dans $\mathbb{R}$ l’équation suivante : $$(E): \arctan (x+1)+\arctan (x-1)=\dfrac{\pi}{4}$$
- Montrer que l’équation $( E )$ admet une solution unique dans $\mathbb{R}$ et qu’elle appartient $]0,1[$.
- Résoudre l’équation $(E)$.
- En déduire $\tan \left(\dfrac{\pi}{12}\right)$.

On considère la fonction $f_{n}$ définie par : $$f_{n}(x)=\sqrt[n]{\arctan (x)}-\arccos (\sqrt[n]{x})\,\,\text{ où }\,\,\left(n \in \mathbb{N}^{*}\right)$$
- Montrer que $f_{n}$ est une bijection de $[0,1]$ vers un intervalle $J$ à déterminer.
-
- Montrer que pour tout $n \in \mathbb{N}^{*}$, l’équation $f_{n}(x)=0$ admet une unique solution $a_{n}$ dans l’intervalle $] 0,1$.
- Montrer que $\left(\forall n \in \mathbb{N}^{*}\right)(\forall x \in] 0,1[$ ): $\sqrt[n]{x}<\sqrt[n+1]{x}$
- En déduire que : $\left( {\forall n \in {\mathbb{N}^*}} \right)\left( {\forall x \in \left] {0,1} \right[} \right):{f_n}\left( x \right) < {f_{n + 1}}\left( x \right)$
- Comparer $a_n$ et $a_{n+1}$

Soient $a$ et $b$ deux nombres réels tels que : $ab<1$. On pose : $$\alpha=\arctan(a) \quad \text{ et } \quad \beta=\arctan(b)$$
- Montrer que $\cos (\alpha+\beta)=\cos (\alpha) \cos (\beta)(1-a b)$
- En déduire que $-\dfrac{\pi}{2}<\alpha+\beta<\dfrac{\pi}{2}$
- Montrer que : $\arctan(a)+\arctan(b)=\arctan\left(\dfrac{a+b}{1-a b}\right)$
- Calculer $2 \arctan \left(\dfrac{1}{4}\right)+\arctan \left(\dfrac{1}{7}\right)+2 \arctan \left(\dfrac{1}{13}\right)$
Limite d’une fonction en un point
- Calculer les limites suivantes :
\[
\begin{align*}
\bullet & \quad \lim_{x \to -1} x^3 -x + 2 &\quad\bullet\quad & \lim_{x \to 2} \frac{x^2 -3x + 2}{\sqrt{x} -\sqrt{2}}\\
\bullet & \quad \lim_{x \to 1} \frac{3x \sin(x^2 -1)}{x^2 -1}&\quad\bullet\quad &\lim_{x \to 0} \frac{\sqrt{x+1} -1}{\tan x} \\
\bullet & \quad \lim_{x \to \frac{\pi}{2}} \left(x -\frac{\pi}{2}\right) \tan\frac{x}{2}
\end{align*}\] - Déterminez la valeur de $a$ pour que la fonction $f$ admette une limite en $x=1$.
\[\left\{ \begin{align*}
& f\left( x \right) = \frac{{{x^2} – 3x + a}}{{x – 1}} &;& &{x > 1}\\
& f\left( x \right) = x + 1&;& &{x \le 1}
\end{align*} \right.\]
- Calculons les limites suivantes :
\[\begin{align*}\bullet & \quad \lim_{x \to -1} (x^3 – x + 2) = (-1)^3 -(-1) + 2 = 2. \\
\bullet & \quad \mathop {\lim }\limits_{x \to 2} \frac{{{x^2} -3x + 2}}{{\sqrt x -\sqrt 2 }} = \mathop {\lim }\limits_{x \to 2} \frac{{\left( {x -1} \right)\left( {x -2} \right)\left( {\sqrt x + \sqrt 2 } \right)}}{{x -2}} = 2\sqrt 2. \\
\bullet & \quad \mathop {\lim }\limits_{x \to 1} \frac{{3x\sin \left( {{x^2} -1} \right)}}{{x -1}} = \mathop {\lim }\limits_{x \to 1} 3x.\frac{{\sin ({x^2} -1)}}{{{x^2} -1}}.\left( {x + 1} \right) = 3 \times 1 \times 2 = 6. \\
\bullet & \quad \mathop {\lim }\limits_{x \to \frac{\pi }{2}} \left( {x -\frac{\pi }{2}} \right)\tan x = \mathop {\lim }\limits_{y \to 0} y\tan \left( {y + \frac{\pi }{2}} \right) = \mathop {\lim }\limits_{y \to 0} \frac{{ -y}}{{\sin y}} \times \cos y = -1. \\
\bullet & \quad \mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {x + 1} -1}}{{\tan x}} = \mathop {\lim }\limits_{x \to 0} \frac{{\cos x}}{{\sin x}} \times \frac{x}{{\sqrt {x + 1} + 1}} = \mathop {\lim }\limits_{x \to 0} \frac{x}{{\sin x}} \times \frac{{\cos x}}{{\sqrt {x + 1} + 1}} = 1 \times \frac{1}{2} = \frac{1}{2}.\end{align*}\] - Déterminons la valeur de $a$ pour que la fonction $f$ admette une limite en $x=1.$
On a : $\displaystyle\lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = \ell,$ et comme $\displaystyle\lim_{x \to 1^-} f(x)=2,$ donc $1$ est une racine du polynôme $(x^2-3x+a)$, alors $1-3+a=0$, donc $a=2$.
\[
\lim_{x \to x_0} f(x) =\ell \iff \Big( (\forall \varepsilon > 0)(\exists \delta > 0)(\forall x \in D_f);\,\, 0<|x – x_0| < \delta \implies |f(x) – \ell| < \varepsilon\Big)
\]
Montrons en utilisant la définition que : $\lim_{x \to 1} f(x)=2$
Soit $I=]1-\dfrac{1}{2};1+\dfrac{1}{2}[=]\dfrac{1}{2};\dfrac{3}{2}[$. On a pour tout $x\in I : $ \[\left| {f\left( x \right) – 2} \right| = \left| {x\left( {x – 1} \right)\left( {x + 1} \right)} \right|\]
\[\begin{array}{l}
\frac{1}{2} < x < \frac{3}{2} \Rightarrow \left| x \right| < \frac{3}{2}\\
\frac{{ – 1}}{2} < x – 1 < \frac{1}{2} \Rightarrow \left| {x – 1} \right| < \frac{1}{2}\\
\Rightarrow \frac{3}{2} < x + 1 < \frac{5}{2} \Rightarrow \left| {x + 1} \right| < \frac{5}{2}\\
\Rightarrow \left| x \right|\left| {x – 1} \right|\left| {x + 1} \right| < \frac{5}{4}\left| {x – 1} \right|
\end{array}\]
\bullet&\quad \lim_{x \to x_0} (f(x) + g(x)) = \ell + \ell’,\\
\bullet&\quad \lim_{x \to x_0} (f(x) \times g(x)) =\ell \times \ell’,\\
\bullet&\quad \lim_{x \to x_0} \frac{f(x)}{g(x)} = \frac{\ell}{\ell’}\,\text{ avec }\, \ell’\neq 0.\end{aligned}\]
\bullet&\quad\mathop {\lim }\limits_{x \to 0} \frac{{\sin ax}}{{ax}} = 1\\
\bullet&\quad\mathop {\lim }\limits_{x \to 0} \frac{{1 – \cos x}}{{{x^2}}} = \frac{1}{2}\\
\bullet&\quad\mathop {\lim }\limits_{x \to 0} \frac{1}{{\tan x}} = 1
\end{aligned}\]
Continuité d’une fonction en un point
Dans la figure 1, nous disons que $f$ est non continue en $x_0$.
Dans la figure 2, nous disons que $f$ est continue en $x_0$.
Dans la figure 1, nous avons :\[
\lim_{x \to x_0^+} f(x) = f(x_0) \quad \text{et} \quad \lim_{x \to x_0^-} f(x) = f(x_0)\]
Cela implique que $f$ est n’est pas continue en $x_0.$
Dans la figure 2, nous avons :\[
\lim_{x \to x_0^+} f(x) \neq \lim_{x \to x_0^-} f(x)\]
Cela implique que $f$ est continue en $x_0.$
\lim_{x \to x_0} f(x) = f(x_0)\]Alors $f$ est dite continue en $x_0$.
La continuité à gauche et la continuité à droite
f\left( x \right) &= \frac{{\left| {{x^2} -4} \right|}}{{x -2}} \quad ;\quad x\neq 2\\
f\left( 2 \right) &= 4
\end{align*} \right.\]Étudier la continuité de $f$ à droit et à gauche du point $2$.
Solution : Calcul de la limite :
\[\begin{align*}
&\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{\left| {{x^2} -4} \right|}}{{x -2}} = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{\left( {x -2} \right)\left( {x + 2} \right)}}{{x -2}} = 4 = f\left( 2 \right)\\
&\mathop {\lim }\limits_{x \to {2^-}} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^-}} \frac{{\left| {{x^2} -4} \right|}}{{x -2}} = \mathop {\lim }\limits_{x \to {2^-}} \frac{{ -\left( {x -2} \right)\left( {x + 2} \right)}}{{x -2}} = -4
\end{align*}\]Donc $f$ est continue à droit du point $2$, et n’est pas continue à gauche du point $2$.
Puissance d’un nombre relatif
$$a^{n}=\underbrace{a \times a \times \ldots \ldots \times a}_{n \text { facteurs }}$$
$a^n$ se lit « $a$ puissance $n$ » ou « $n$ exposant $n$ »
- Si $n=1$, alors $a^1=a$.
- Si $n=0$ et $a \neq 0$ alors $a^0=1$.
- $a$ est la base de la puissance $a^n$.
- $n$ est l’exposant de la puissance $a^n$.
- $0^0$ n’existe pas.
- $a^2$ se lit aussi $a$ au carré.
- $a^3$ se lit aussi $a$ au cube.
Exemples :
$\quad\bullet\quad 3^{4}=\underbrace{3 \times 3 \times 3 \times 3}_{4 \text { fois le nombre } 3}=81$
$\quad\bullet\quad(-2)^3=\underbrace{(-2)\times(-2)\times(-2)}_{3 \text { fois le nombre } -2}=-8$
$\quad\bullet\quad (-7)^1=-7$
$\quad\bullet\quad \left(-9\right)^0=1$
Signe d’une puissance
- Si $a$ est positif, alors $a^n$ est positif.
- Si $a$ est négatif, alors :
- Si $n$ est pair, alors $a^n$ est positif.
- Si $n$ est impair, alors $a^n$ est négatif.
Exemples :
- La puissance $\left( -12 \right)^{17}$ est négatif, car la base est négatif et l’exposant est impair.
- La puissance $\left( -3 \right)^{48}$ est positif, car l’exposant est pair.
- La puissance $(17,6)^{21}$ est positif, car la base est positif.
Puissances de 10
- ${10^n} = 1\underbrace {00………0}_{n\,\,\text{zéros}}$
- $10^0=1$ et $10^1=10$
Exemples :
$\quad\bullet\quad$ $10^5=1\underbrace{00000}_{5\text{ zéros}}$
$\quad\bullet\quad$ $10^7=1\underbrace{0000000}_{7\text{ zéros}}$
$\quad\bullet\quad$ $1\underbrace{000000000}_{9\text{ zéros}}=10^9$
$\quad\bullet\quad$ $1\underbrace{0000}_{4\text{ zéros}}=10^4$
$\quad\bullet\quad$ $10^5 =100000$
Opérations sur les puissances
$$\begin{aligned}
&\bullet\quad a^n \times a^m = a^{n+m}\\
&\bullet\quad a^n \times b^n = (a \times b )^{n}\\
&\bullet\quad \left( a^n\right)^m=a^{n\times m}\\
&\bullet\quad \dfrac{a^n}{a^m}= a^{n-m}, \text{ avec } (n>m)\\
&\bullet\quad \dfrac{a^n}{b^n}= \left(\dfrac{a}{b}\right)^{n}\end{aligned}$$
&\bullet\quad 10^n \times 10^m = 10^{n+m}\\
&\bullet\quad \left( 10^n\right)^m=a^{10\times m}\\
&\bullet\quad \dfrac{10^n}{10^m}= 10^{n-m}
\end{aligned}$$
Exemples :
$$\begin{aligned}
&\bullet\quad 10^9 \times 10^5= 10^{9+5}=10^{14}\\
&\bullet\quad 2^7 \times 5^7= (2 \times 5)^7=10^7\\
&\bullet\quad \left( 10^3\right)^4=10^{3 \times 4} =10^{12}\\
&\bullet\quad \dfrac{10^8}{10^3}=10^{8-3}=10^5\\
&\bullet\quad \dfrac{21^{13}}{7^{13}}=\left(\dfrac{21}{7}\right)^{13}=3^{13}
\end{aligned}$$
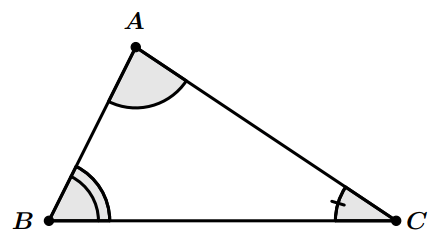
Somme des mesures des angles d’un triangle
Exemple : Soit $ABC$ un triangle :
Triangles particuliers
Triangle rectangle
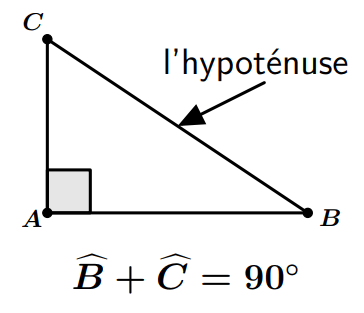
- Si un triangle est rectangle, alors ses deux angles aigus sont complémentaires.
- Si un triangle a deux angles complémentaires, alors il est rectangle.
Triangle isocèle
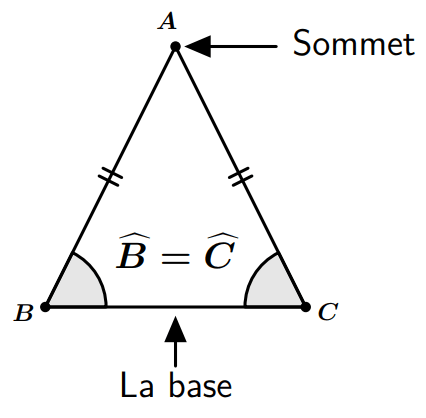
- Si un triangle est isocèle, alors les deux angles à la base ont la même mesure.
- Si un triangle a deux angles égaux, alors il est isocèle.
Triangle équilatéral
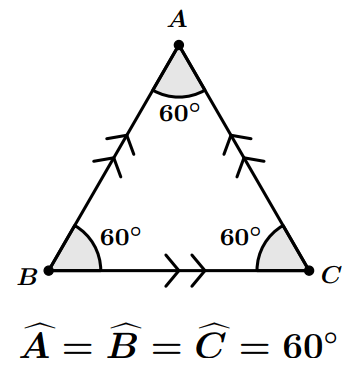
- Si un triangle est équilatéral, alors chacun de ses angles mesure $60^\circ$.
- Si un triangle a trois angles égaux, alors il est équilatéral.
Angles
- L’origine de ses deux demi-droites est le sommet de l’angle.
- Ces deux demi-droites sont les côtés de l’angle.
Exemple :
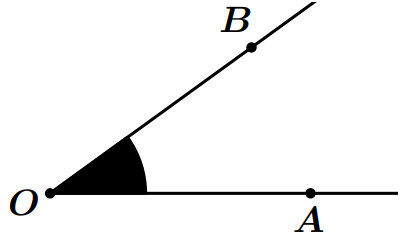
- L’angle noir est noté $\widehat {AOB}$.
- $O$ est le sommet de l’angle $\widehat {AOB}$.
- Les demi-droites $[OA)$ et $[OB)$ sont les cotés de l’angle $\widehat {AOB}$.
- Pour mesurer un angle on utilise le rapporteur.
- L’unité de mesure des angles est le degré.
Angles particuliers
Angle nul
- La mesure d’un angle nul est égale à $0^\circ$.
- Les cotes d’un angle nul sont confondues.

Angle aigu
Angle droit
Angle obtus

Angle plat

Angle plein
Relation entre deux angles
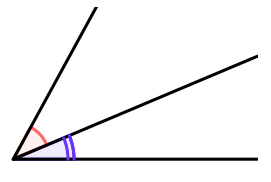
Angles adjacents
- ont le même sommet;
- ont un côté commun;
- sont situés de part et d’autre de ce côté commun.
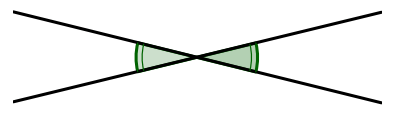
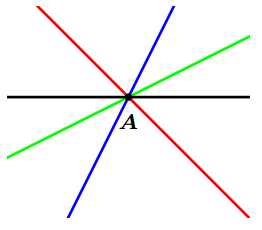
Angles opposés par le sommet
- Deux angles opposés par le sommet sont deux angles qui ont le même sommet et leurs côtés sont dans le prolongement l’un de l’autre.
- Deux angles opposés par le sommet sont égaux.
Angles complémentaires
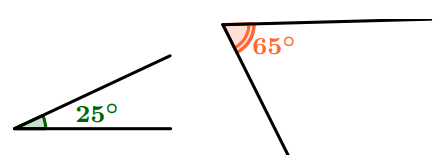
Angles supplémentaires
Droite
- Par deux points distincts $A$ et $B$, passe une et une seule droite, on la note: $(A B)$ ou $(B A)$.

- Si $M$ est un point de la droite $(A B)$, alors on note $M \in(A B)$ et se lit: $M$ appartient à la droite $(A B)$.
- Une droite est illimitée des deux côtés.
- Par un point, passe une infinité de droites.
- Tous les points qui appartiennent à la même droite, sont des points alignés.

Les points $A, B, C$ et $E$ sont alignés.
Demi-droite

- La partie de la droite $(D)$ coloriée en rouge, limitée par le point $A$, et passant par le point $B$ est appelée: La demi-droite d’origine $A$, et qui passe par le point $B$. On la note: $[A B)$
- La partie de la droite $(D)$ coloriée en vert est la demi-droite $[A C)$
Segment-Milieu d’un segment
![Segment [AB] délimité par deux points.](https://mathxi.com/wp-content/uploads/2024/09/segment.png)
![Milieu M du segment [AB].](https://mathxi.com/wp-content/uploads/2024/09/milieu-segment.png)
Positions relatives de deux droites
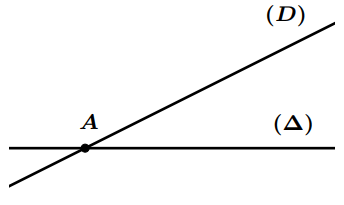
Droites sécantes
- Deux droites $(D)$ et $(\Delta)$ qui se coupent en un seul point, sont appelées droites sécantes.
- On dit aussi que les droites $(D)$ et $(\Delta)$ sont sécantes en $A$
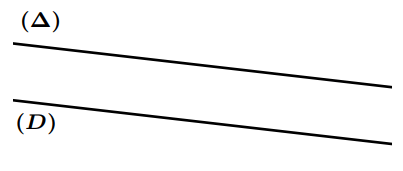
Droites parallèles

Droites perpendiculaires
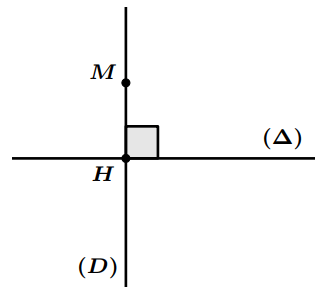
- Le point $H$ est appelé le projeté orthogonal du point $M$ sur la droite ($\Delta$)
- La longueur $M H$ est appelée la distance du point $M$ à la droite ($\Delta$)
Propriétés :
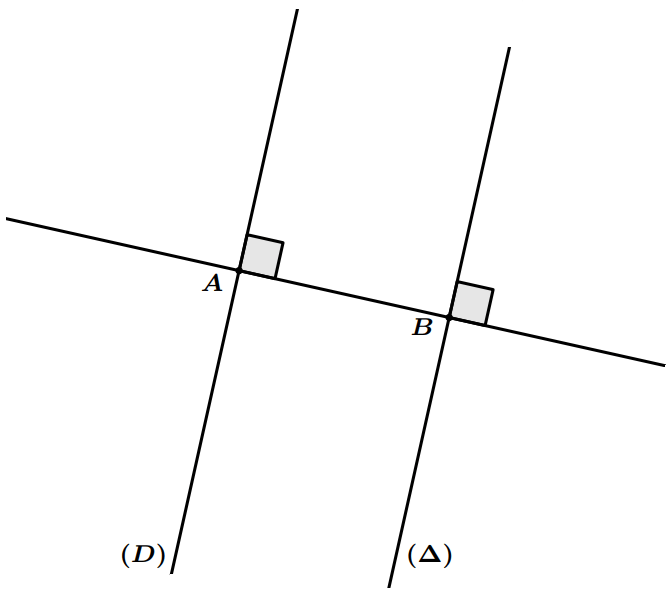
- Si deux droites sont parallèles, alors toute droite perpendiculaire à lune est perpendiculaire à l’autre.
- Si deux droites sont parallèles, alors toute droite parallèle à l’une est parallèle à l’autre,
- Si deux droites sont perpendiculaires, alors toute droite perpendiculaire à lune est parallèle à l’autre.
- Si deux droites sont perpendiculaires, alors toute droite parallèle à l’une est perpendiculaire à l’autre.
Exemple : Dans la figure ci-dessous, on a : $(D)\perp (AB)$ et $(\Delta)\perp (AB)$, donc : $(D)\parallel (\Delta)$