$ABC$ un triangle tels que : $AB=3cm$, $AC=4cm$ et $BC=5cm$.
- Quelle est la nature du triangle $ABC$? Justifier.
- Calculer les rapports trigonométriques de l’angle $\widehat{ACB}$.

$ABC$ est un triangle rectangle en $A$ tels que : $AC=4$ et $\sin \widehat{ABC}=0,625$.
- Calculer $BC$.
- Calculer $AB$.

$ABC$ est un triangle rectangle en $A$ tels que : $AC=3$ et $\tan \widehat{ABC}=0,75$.
- Calculer $AB$.
- Calculer $BC$.

$\alpha$ est la mesure d’un angle aigu.
- Sachant que : $\cos\alpha=0,2$, calculer : $\sin\alpha$ et $\tan\alpha$.
- Sachant que : $\tan\alpha=\sqrt{15}$, calculer : $\cos\alpha$ et $\sin\alpha$.

Simplifier les expressions suivantes tel que $\alpha$ est la mesure d’un angle aigu.
- $A = {\left( \sin \alpha + \cos \alpha \right)^2} + {\left( \sin \alpha – \cos \alpha \right)^2}$
- $B = {\cos^2}\alpha + 2{\sin^2}\alpha – 1$
- $C = {\cos^4}\alpha + 2{\cos^2}\alpha \cdot {\sin^2}\alpha + {\sin^4}\alpha$
- $D = \dfrac{1}{1 + \sin \alpha} + \dfrac{1}{1 – \sin \alpha} – \dfrac{2}{\cos^2 \alpha}$
- $E = \sqrt{\cos \alpha + 1} \times \sqrt{1 – \cos \alpha} \times \dfrac{1}{\sin \alpha}$
- $F = \dfrac{{\cos^4 \alpha} – {\sin^4 \alpha}}{{\cos^2 \alpha} – {\sin^2 \alpha}}$

$\alpha$ est la mesure d’un angle aigu.
- Montrer que : $\cos^2 \alpha = \dfrac{1}{1 + \tan^2 \alpha}$
- Montrer que : $\sin^2 \alpha = \dfrac{\tan^2 \alpha}{1 + \tan^2 \alpha}$
- Sachant que : $\tan \alpha = 4\sqrt{3}$, calculer : $\sin \alpha$ et $\cos \alpha$.

- Avec la calculatrice, calculer $\sin 30^\circ$.
- En déduire $\cos 30^\circ$ et $\tan 30^\circ$.
- En déduire les rapports trigonométriques de l’angle $60^\circ$.

Simplifier les expressions suivantes :
$$
\begin{aligned}
A &= \cos 25^\circ + \cos 70^\circ – \sin 65^\circ + \sin 20^\circ \\
B &= \sin 80^\circ + 7{\sin^2 50^\circ} – \cos 10^\circ + 7{\sin^2 40^\circ}
\end{aligned}$$

$ABC$ un triangle rectangle en $C$ tel que : $AC=2\sqrt{5}$ et $BC=4$.
- Calculer $AB$.

$ABC$ est un triangle rectangle isocèle en $A$ tels que : $AB=4cm$. Soit $M$ le milieu de $[BC]$.
- Faire la figure.
- Calculer $BC$.
- En déduire $AM$.

$ABCD$ est un carré de diagonale $4cm$.
- Calculer $AB$.

Soit $EFP$ un triangle rectangle en $P$ tel que : $EF=5$ et $EP=4$.
- Calculer $FP$.
- Soit $H$ le projeté orthogonal de $P$ sur la droite $(EF)$.
- Vérifier que : $\left(5-FH\right)^2-FH^2=7$.
- En déduire que : $FH=1,8$.
- Calculer $PH$.

- Soit $MNP$ un triangle tel que : $MN=20cm$, $MP=12cm$ et $NP=16cm$. Le triangle $MNP$ est-il rectangle? Justifier la réponse.
- Soit $RST$ un triangle tel que : $ST=6cm$, $RS=4cm$ et $RT=4,5cm$. Le triangle $RST$ est-il rectangle? Justifier la réponse.

Soit $ABC$ un triangle tel que : $AB=2\sqrt{3}$, $BC=4$ et $AC=2$.
- Montrer que le triangle $ABC$ est rectangle en $A$.
- Soit $H$ le projeté orthogonal de $A$ sur la droite $(BC)$.
- Calculer $AH$.
- En déduire $CH$.

Soit $ABC$ un triangle, tels que :
$AB=5cm$, $AC=8cm$, $BC=6cm$
$I$ un point de $[AB]$ tel que $IA=2cm$, et
$J$ un point de $[AC]$, tel que $(IJ)\parallel (BC)$
- Faire une figure.
- Calculer les distances $JA$, $JC$ et $IJ$

Soit $ABC$ un triangle tels que :
$AB=5cm$; $AC=10cm$ et $BC=8cm$.
$E$ un point de $[AB]$ tel que $AE=2cm$ et $F$ un point de $[AC]$ tel que $AF=4cm $
- Faire une figure.
- Montrer que : $(EF)\parallel(BC)$.
- La droite passant par le point $B$ parallèlement à $(EC)$ coupe $(AC)$ en $K$. Calculer $CK$

$ABCD$ est un parallélogramme.
Soient $E$ et $I$ deux points de $[AB]$ et $[AC]$ respectivement tels que:
$(IE)\parallel (BC)$ et $AB=10$; $BC=8$; $AI=3$ et $AE=6$.
- Calculer $AC$ et $IE$.
- Soit $F$ un point de $[AD]$ tel que : $AF=4,8$.
- Comparer les rapports : $\dfrac{AI}{AC}$ et $\dfrac{AF}{AD}$.
- En déduire que les droites $(IF)$ et $(DC)$ sont parallèles.
- Montrer que les droites $(BD)$ et $(EF)$ sont parallèles.

Dans la figure suivante les droites $(AC)$ et $(EF)$ sont parallèles.
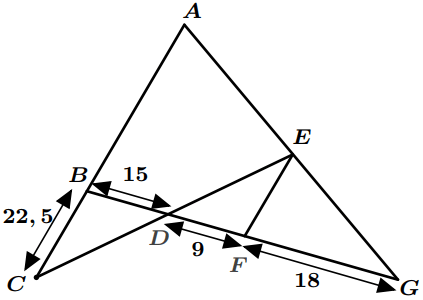 Calculer $AB$.
Calculer $AB$.
Dans la figure suivante :
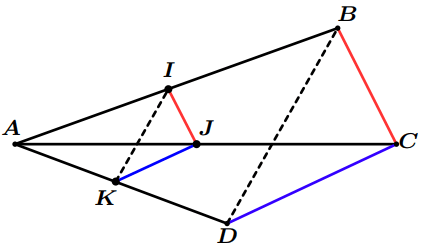
- Les droite $(IJ)$ et $(BC)$ sont parallèles.
- Les droite $(JK)$ et $(CD)$ sont parallèles.
Montrer que les droites $(IK)$ et $(BD)$ sont parallèles.

Dans la figure suivante :
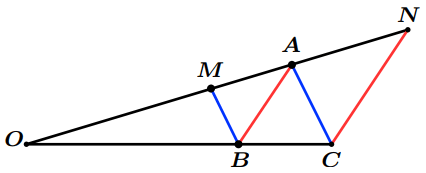
- Les droite $(MB)$ et $(AC)$ sont parallèles.
- Les droite $(AB)$ et $(NC)$ sont parallèles.
En utilisant le théorème de Thalès, Démontrer que : $OA^2=OM\times ON$.
Epreuve de Mathématiques
Session de rattrapage 2025
Durée : 4 heures

Partie I :
On considère la fonction $f$ définie sur l’intervalle $I = [0; +\infty[$ par :
$$
f(0) = 0 \quad \text{et} \quad f(x) = \frac{x^2 \ln x}{x^2 + 1} \quad \text{si} \quad x \in ]0; +\infty[
$$
Et soit $(C)$ la courbe représentative de la fonction $f$ dans un repère orthonormé $(O, \vec{i}, \vec{j})$.
-
- Étudier la continuité de $f$ à droite en 0
- Étudier la dérivabilité de $f$ à droite en 0 puis interpréter graphiquement le résultat obtenu.
- Calculer $\displaystyle\lim_{x \to +\infty} f(x) $ et $\displaystyle\lim_{x \to +\infty} \dfrac{f(x)}{x}$ puis interpréter graphiquement le résultat obtenu.
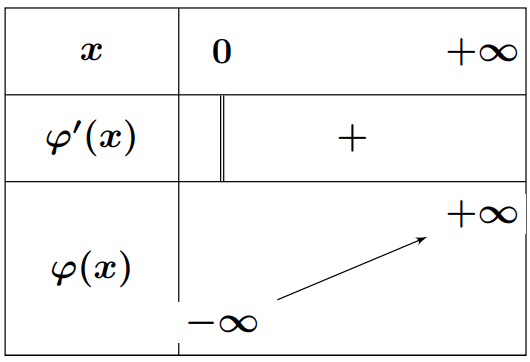
- Soit $\varphi$ la fonction définie sur $]0; +\infty[$ par : $ \varphi(x) = x^2 + 1 + 2 \ln x $
- Dresser le tableau de variations de $\varphi$
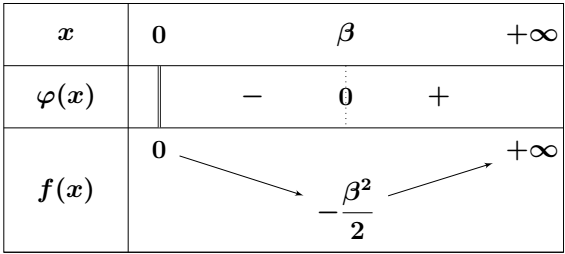
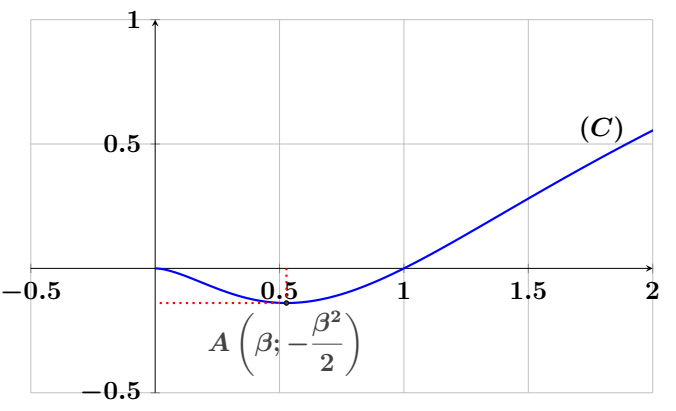
- Montrer que l’équation $ \varphi(x) = 0 $ admet une solution unique $\beta$ appartenant à l’intervalle
$ \left[ \dfrac{1}{2} ; \dfrac{1}{\sqrt{3}} \right] $ (On donne $ \ln 2 \simeq 0{,}7 $ et $ \ln 3 \simeq 1{,}1 $) - Montrer que : $ f(\beta) = -\dfrac{\beta^2}{2} $
-
- Montrer que $f$ est dérivable sur $]0; +\infty[$ et que $\left(\forall x \in ]0; +\infty[\right),\quad f'(x) = \dfrac{x \varphi(x)}{(x^2 + 1)^2}$
- Donner le tableau de variations de $f$
- Montrer que $ \dfrac{1}{\beta} $ est l’unique solution de l’équation $ f(x) = \dfrac{1}{2} $ sur $ ]\beta; +\infty[ $
- Montrer que la droite d’équation $ y = \beta x -\dfrac{1}{2} $ est la tangente à la courbe $(C)$ au point d’abscisse $ \dfrac{1}{\beta} $
- Représenter graphiquement la courbe $(C)$ dans le repère $(O, \vec{i}, \vec{j})$
(On admet que la courbe $(C)$ possède deux points d’inflexion)
Partie II :
On pose : $ J = \left] \sqrt{3}; 2 \right] \quad \text{et} \quad \alpha = \dfrac{1}{\beta}$
Soit $g$ la fonction définie sur $]0; +\infty[$ par : $ g(x) = \sqrt{e^{1+\frac{1}{x^2}}} $
-
- Étudier les variations de $g$
- Montrer que : $\left(\forall x \in J\right), \quad \sqrt{3} < g(x) < 2$
(On donne $ \sqrt{3} \simeq 1{,}73$, $ e^{1/2} \simeq 1{,}95$ et $ e^{5/6} \simeq 1{,}87$)
-
- En utilisant le résultat de la question I.3-c), montrer que : $ g(\alpha) = \alpha $
- Montrer que : $\left( {\forall x \in J} \right);\quad \left| {g’\left( x \right)} \right| \le \dfrac{2}{{3\sqrt 3 }}$
- En déduire que : $\left( {\forall x \in J} \right);\quad \left| {g\left( x \right) -\alpha } \right| \le \dfrac{2}{{3\sqrt 3 }}\left| {x -\alpha } \right|$
- On considère la suite $(x_n)_{n\in\mathbb{N}}$ définie par : $$x_0=\dfrac{7}{4}\quad\text{et pour tout } n\in\mathbb{N},\quad x_{n+1}=g(x_n)$$
- Montrer que : $\left( {\forall x \in \mathbb{N}} \right);\quad {x_n} \in J$
- Montrer par récurrence que : $\left( {\forall x \in \mathbb{N}} \right);\quad \left| {{x_n} -\alpha } \right| \le {\left( {\dfrac{2}{{3\sqrt 3 }}} \right)^n}\left| {{x_0} -\alpha } \right|$
- En déduire que la suite $(x_n)_{n\in\mathbb{N}}$ converge vers $\alpha$.

On considère la suite numérique $\left(u_n\right)_{n \geq 2}$ définie par: $(\forall n \geq 2) \quad u_n=\dfrac{1}{n} \displaystyle\sum_{k=1}^{n-1} \ln \left(\dfrac{k}{n}\right)$
- Soit $n$ un entier naturel supérieur ou égal à 2.
- Montrer que pour tout entier $k \displaystyle\in\{1,2, \ldots, n-1\}$
et pour tout réel $x \in\left[\dfrac{k}{n} ; \dfrac{k+1}{n}\right]$, on a :
$$\ln \left(\dfrac{k}{n}\right) \leq \ln (x) \leq \ln \left(\dfrac{k+1}{n}\right)$$ - En déduire que : $$\forall k \displaystyle\in\{1,2, \ldots, n-1\};\quad \dfrac{1}{n} \ln \left(\dfrac{k}{n}\right) \leq \displaystyle\int_{\frac{k}{n}}^{\frac{k+1}{n}} \ln (x) d x \leq \dfrac{1}{n} \ln \left(\dfrac{k+1}{n}\right)$$
- Montrer que pour tout entier $k \displaystyle\in\{1,2, \ldots, n-1\}$
-
- Montrer que : $$(\forall n \geq 2);\quad \dfrac{1}{n} \displaystyle\sum_{k=1}^{n-1} \ln \left(\dfrac{k}{n}\right) \leq \displaystyle\int_{\frac{1}{n}}^1 \ln (x) d x \leq \dfrac{1}{n} \sum_{k=2}^n \ln \left(\dfrac{k}{n}\right)$$
- En déduire que : $$(\forall n \geq 2) ;\quad u_n \leq \displaystyle\int_{\frac{1}{n}}^1 \ln (x) d x \leq u_n-\dfrac{1}{n} \ln \left(\dfrac{1}{n}\right)$$
- Montrer que : $$(\forall n \geq 2) ;\quad -1+\dfrac{1}{n} \leq u_n \leq-1+\dfrac{1}{n}-\dfrac{1}{n} \ln \left(\dfrac{1}{n}\right)$$
- Déterminer $\displaystyle\lim _{n \rightarrow+\infty} u_n$

Soit $\theta\in\left[0,\pi\right[$
Partie I:
On considère dans l’ensemble des nombres complexes $\mathbb{C}$ l’équation $(E_\theta)$ d’inconnue $z$
$$(E_\theta):\quad z^2+(1-i)e^{i\theta}z-ie^{i2\theta}=0$$
-
- Vérifier que : $\left(E_\theta\right) \Leftrightarrow\left(2 z+(1-i) e^{i \theta}\right)^2=\left((1+i) e^{i \theta}\right)^2$
- En déduire les deux solutions $z_1$ et $z_2$ de l’équation $\left(E_\theta\right)$ avec $\operatorname{Im}\left(z_1\right) \leq 0$
-
- Montrer que : $\dfrac{z_1+1}{z_2+i}=-\tan \left(\dfrac{\theta}{2}\right)$
- En déduire la forme exponentielle du nombre complexe : $\dfrac{z_1+i z_2}{z_2+i}$
Partie II:
Dans le plan complexe $(\mathcal{P})$ muni d’un repère orthonormé direct $(O, \vec{u}, \vec{v})$, on considère les points $A, B$, et $C$ d’affixes respectives $a=e^{i \theta}, b=(1+i) e^{i \theta}$ et $c=b-a$
Soient $m$ un nombre réel de $] 0 ; 1\left[, R\right.$ la rotation de centre $O$ et d’angle $\dfrac{\pi}{2}$ et le point $Q$ d’affixe $q=m e^{i \theta}$
-
- Déterminer l’affixe $p$ du point $P$ l’image du point $Q$ par la rotation $R$
- Vérifier que : $R(A)=C$
- Soit $H$ le point d’affixe $h=\dfrac{m}{m-i} e^{i \theta}$
- Montrer que : $\dfrac{p-a}{h}=\dfrac{m^2+1}{m} i$ et $\dfrac{h-a}{p-a}=\dfrac{1}{m^2+1}$
- En déduire que $H$ est le projeté orthogonal du point $O$ sur la droite ( $A P$ )
- Montrer que : $\dfrac{b-h}{q-h}=\dfrac{1}{m} i$
- En déduire que les droites $(Q H)$ et $(H B)$ sont perpendiculaires.
- Montrer que les points $A, Q, H$ et $B$ sont cocycliques.

On considère dans $\mathbb{Z} \times \mathbb{Z}$ l’équation $$(E): \quad y=\dfrac{a}{b} x-\dfrac{c}{d}$$ où $a, b, c$ et $d$ sont des entiers naturels non nuls vérifiant : $\quad a \wedge b=c \wedge d=1$
- On suppose que l’équation $(E)$ admet une solution $\left(x_0, y_0\right)$
- Montrer que $d$ divise $b c$
- En déduire que $d$ divise $b$
- On suppose que $d$ divise $b$ et on pose : $b=n d$ où $n$ est un entier naturel non nul.
-
- Montrer que qu’il existe $(u, v) \in \mathbb{N} \times \mathbb{N}$ tel que : $d n u-a v=1$
- En déduire que l’ensemble des solutions de l’équation $(E)$ est
$$
S=\Big\{(-v c n+b k ;-u c n+a k) / k \in \mathbb{Z}\Big\}
$$ -
- Résoudre dans $\mathbb{Z}\times \mathbb{Z}$ l’équation $(F): y=\dfrac{3}{2975}x-\dfrac{2}{119}$ (On donne : $2957=119\times 25$)

On rappelle que $\left(M_3(\mathbb{R}),+, \times\right)$ est un anneau unitaire non commutatif de zéro la matrice $O=\left(\begin{array}{lll}0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{array}\right)$ et d’unité la matrice $I=\left(\begin{array}{lll}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right)$.
On munit l’ensemble $E=\Big\{x+y i / x \in \mathbb{Z}\text{ et } y \in \mathbb{Z}\Big\}$ par la loi de composition interne $*$ définie par:
$$\left(\forall\left(x, y, x^{\prime}, y^{\prime}\right) \in \mathbb{Z}^4\right) ;\quad (x+y i) *\left(x^{\prime}+y^{\prime} i\right)=\left(x+(-1)^y x^{\prime}\right)+\left(y+y^{\prime}\right) i$$Partie I :
-
- Vérifier que : $$(1-i) *(3+2 i)=-2+i$$
- Montrer que la loi $*$ n’est pas commutative dans $E$
- Montrer que la loi $*$ est associative dans $E$
- Montrer que $0$ est l’élément neutre pour la loi $*$ dans $E$
-
- Vérifier que :
$$\left(\forall(x, y) \in \mathbb{Z}^2\right);\quad (x+y i) *\left((-1)^{(y+1)} x-y i\right)=0$$ - Montrer que $(E,*)$ est un groupe non commutatif.
- Vérifier que :
Partie II :
Soient les deux ensembles $$F=\Big\{x+2 y i / x \in \mathbb{Z}\,\,\text{ et }\,\,y \in \mathbb{Z}\Big\}$$
et
$$
G=\left\{M(x, y)=\left(\begin{array}{lll}
1 & x & y \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right) / x \in \mathbb{Z} \text { et } y \in \mathbb{Z}\right\}
$$
-
- Montrer que $F$ est un sous-groupe de $(E,*)$
- Montrer que la loi $*$ est commutative dans $F$
- Soit $\varphi$ l’application définie de $F$ vers $M_3(\mathbb{R})$ par:$$
\forall(x, y) \in \mathbb{Z}^2 ;\quad \varphi(x+2 y i)=M(x, y)
$$- Montrer que $\varphi$ est un homomorphisme de $(F, *)$ vers $\left(M_3(\mathbb{R}), \times\right)$
- Montrer que $\varphi(F)=G$
- En déduire que $(G, \times)$ est un groupe commutatif.
Epreuve de Mathématiques
Session normale 2025
Durée : 4 heures

On considère la fonction numérique $f$ définie sur $\mathbb{R}$ par :
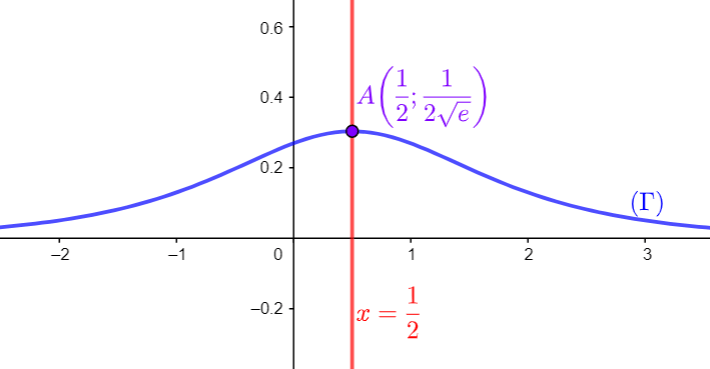
$$f(x) = \dfrac{e^x}{e^{2x} + e}$$ et soit $(\Gamma)$ sa courbe représentative dans un repère orthogonal $(O; \vec{i}, \vec{j})$.
Partie I :
-
- Montrer que : $\left(\forall x \in \mathbb{R}\right);~~f(1-x) = f(x)$.
- Interpréter graphiquement le résultat obtenu.
- Calculer $\displaystyle\lim_{x \to-\infty} f(x)$ puis en déduire $\displaystyle\lim_{x \to+\infty} f(x)$.
- Interpréter graphiquement les deux résultats obtenus.
-
- Montrer que : $\left(\forall x \in \mathbb{R}\right);~~f'(x) = f(x) \dfrac{1-e^{2x-1}}{1 + e^{2x-1}}$.
- Donner les variations de $f$ puis en déduire que :
$$\left(\forall x \in \mathbb{R}\right);~~0 < f(x) < \dfrac{1}{2}.$$
- Représenter graphiquement la courbe $(\Gamma)$.
(On prendra $\left\|\vec{i}\right\|=1\,cm,\, \left\|\vec{j}\right\|=2\,cm,\,\dfrac{1}{2\sqrt{e}} \approx 0.30, \dfrac{1}{1+e} \approx 0.27$).
-
- Montrer que : $\displaystyle\int_{0}^{1/2} f(x)\, dx = \int_{1/2}^1 f(x)\, dx$.
- En déduire que $\displaystyle\int_{0}^{1} f(x)\, dx = 2 \int_{0}^{1/2} f(x)\, dx$.
-
- En effectuant le changement de variable : $t = e^x $, montrer que : $$\int_{0}^{1/2} f(x)\, dx = \int_{1}^{\sqrt{e}} \dfrac{dt}{t^2 + e}.$$
- Montrer que : $$\int_{0}^{1/2} f(x)\, dx = \dfrac{1}{\sqrt{e}} \left(\arctan\left(\sqrt{e}\right)-\dfrac{\pi}{4}\right).$$
- En déduire l’aire, en $cm^2$, du domaine plan délimité par $(\Gamma)$, les droites d’équations respectives : $ x=0$, $x=1$, et $y=0$.
Partie II :
On considère la suite $(u_n)_{n\in\mathbb{N}}$ définie par :
$$u_0 \in \left]0; \dfrac{1}{2}\right[,\, \text{ et }\, \left(\forall n \in \mathbb{N}\right);\,\, u_{n+1} = f(u_n)$$
- En utilisant le résultat de la question I.2-a), montrer que :
$$\left(\forall x \in \mathbb{R}\right);\,\, |f'(x)| \leq f(x)$$ -
- Montrer que :
$$\left(\forall x \in \left[0; \dfrac{1}{2}\right]\right);\,\, 0 \leq f'(x) < \dfrac{1}{2}$$ - Montrer que la fonction $g : x\mapsto g(x)=f(x)-x$ est strictement décroissante sur $\mathbb{R}$.
- En déduire qu’il existe un unique réel $\alpha \in \left]0;\dfrac{1}{2}\right[$ tel que : $f(\alpha)=\alpha$
- Montrer que :
-
- Montrer que : $\left(\forall n \in \mathbb{N}\right); \quad 0 < u_n < \dfrac{1}{2}$
- Montrer que : $\left(\forall n \in \mathbb{N}\right); \quad |u_{n+1}-\alpha| \leq \dfrac{1}{2} |u_n-\alpha|$
- Montrer par récurrence que : $\left(\forall n \in \mathbb{N}\right); \quad |u_n-\alpha| \leq \left( \dfrac{1}{2} \right)^{n+1}$
- En déduire que la suite $(u_n)_{n \in \mathbb{N}}$ converge vers $\alpha$
Partie III :
On considère la suite numérique $(S_n)_{n \in \mathbb{N}}$ définie par : \[\left( {\forall n \in {\mathbb{N}^*}} \right);\quad {S_n} = \frac{1}{{n\left( {n + 1} \right)}}\sum\limits_{k = 1}^{k = n} {\frac{k}{{{e^{\frac{k}{n}}} + {e^{\frac{{n-k}}{n}}}}}} \]
-
- Vérifier que : $\left( {\forall n \in {\mathbb{N}^*}} \right);\quad {S_n} = \dfrac{1}{{n + 1}}\displaystyle\sum\limits_{k = 1}^{k = n} {\dfrac{k}{n}f\left( {\dfrac{k}{n}} \right)} $
- Montrer que: $$\displaystyle\int_0^1 x f(x) \, dx = \int_0^{1/2}f(x) \, dx$$
(On pourra effectuer le changement de variable : $t = 1-x$)
- Montrer que la suite $(S_n)_{n \in \mathbb{N}}$ est convergente et déterminer sa limite.

Soit $\alpha\in\left[0;2\pi\right[$.
On considère dans l’ensemble des nombres complexes $\mathbb{C}$ l’équation $(E_\alpha)$ d’inconnue $z$ : $$(E_\alpha) : \quad z^2-2^\alpha e^{i\alpha}(1 + 2i)z + i2^{2\alpha + 1} e^{i2\alpha} = 0$$
Partie I:
-
- Vérifier que le discriminant de l’équation $(E_\alpha)$ est : $$\Delta_\alpha = \left(2^{\alpha}e^{i\alpha}(1-2i)\right)^2$$
- En déduire les deux solutions $a$ et $b$ de l’équation $(E_\alpha)$ avec $|a| < |b|$
- Vérifier que $\dfrac{b}{a}$ est un imaginaire pur.
Partie II:
Le plan complexe est rapporté à un repère orthonormé direct $(O ; \vec{u}, \vec{v})$.
On note par $M(z)$ le point d’affixe le nombre complexe $z$.
On pose $\dfrac{b}{a}=\lambda i$ avec $\lambda=\operatorname{Im}\left(\dfrac{b}{a}\right)$.
- On considère les points $A(a), B(b)$ et $H(h)$ avec $\dfrac{1}{h}=\dfrac{1}{a}+\dfrac{1}{b}$.
- Montrer que $: \dfrac{h}{b-a}=-\left(\dfrac{\lambda}{\lambda^2+1}\right) i$ puis en déduire que les droites $(O H) \operatorname{et}(A B)$ sont perpendiculaires.
- Montrer que : $\dfrac{h-a}{b-a}=\dfrac{1}{\lambda^2+1}$ puis en déduire que les points $H, A$ et $B$ sont alignés.
- Soient $I(m)$ le milieu du segment $[O H]$ et $J(n)$ le milieu du segment $[H B]$.
- Montrer que : $\dfrac{n}{m-a}=-\lambda i$.
- En déduire que les droites $(O J)$ et $(A I)$ sont perpendiculaires et que $O J=|\lambda| A I$.
- Soit $K$ le point d’intersection des droites ( $O J$ ) et ( $A I$ )Montrer que les points $K, I, H$ et $J$ sont cocycliques.
- Montrer que les droites $(I J)$ et $(O A)$ sont perpendiculaires.

Soient $p$ un nombre premier impair et $a$ un entier premier avec $p$.
- Montrer que : $\,\,a^{\frac{p-1}{2}} \equiv 1[p]$ ou $a^{\frac{p-1}{2}} \equiv-1[p]$.
- On considère dans $\mathbb{Z}$ l’équation : $\,\,a x^2 \equiv 1[p]$. Soit $x_0$ une solution de cette équation.
- Montrer que : $\,\,x_0{ }^{p-1} \equiv 1[p]$.
- En déduire que : $\,\,a^{\frac{p-1}{2}} \equiv 1[p]$.
- Soit $n$ un entier naturel non nul.
- Montrer que si $p$ divise $2^{2 n+1}-1$ alors $2^{\frac{p-1}{2}} \equiv 1[p]$.
- En déduire que l’équation $(E):\,\, 11 x+\left(2^{2 n+1}-1\right) y=1$ admet au moins une solution dans $\mathbb{Z}^2$.
- On considère dans $\mathbb{Z}$ l’équation $(F):\,\, x^2+5 x+2 \equiv 0 \quad[11]$.
- Montrer que : $\,\,(F) \Leftrightarrow 2(2 x+5)^2 \equiv 1[11]$.
- En déduire que l’équation $(F)$ n’admet pas de solution dans $\mathbb{Z}$.

On rappelle que $\left(M_3(\mathbb{R}),+, \times\right)$ est un anneau unitaire et non commutatif de zéro la matrice $O=\left(\begin{array}{lll}0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{array}\right)$ et d’unité la matrice $I=\left(\begin{array}{lll}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right)$, et que $\left(M_3(\mathbb{R}),+,.\right)$ est un espace vectoriel réel.
Soient la matrice $A=\left(\begin{array}{ccc}-1 & -1 & 0 \\ -1 & -1 & 0 \\ -1 & 1 & -2\end{array}\right)$ et l’ensemble $E=\{M(x)=I+x A / x \in \mathbb{R}\}$
-
- Vérifier que : $\,\,A^2=-2 A$
- En déduire que : $\,\,\forall(x, y) \in \mathbb{R}^2 ;\,\, M(x) \times M(y)=M(x+y-2 x y)$
-
- Calculer : $\,\,M\left(\dfrac{1}{2}\right) \times\left(\begin{array}{lll}0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1\end{array}\right)$
- En déduire que la matrice $M\left(\dfrac{1}{2}\right)$ n’est pas inversible dans $\left(M_3(\mathbb{R}), \times\right)$
- Montrer que : $E-\left\{M\left(\dfrac{1}{2}\right)\right\}$ est stable pour la multiplication dans $M_3(\mathbb{R})$
(on pourra utiliser l’identité : $\left(x-\dfrac{1}{2}\right)\left(y-\dfrac{1}{2}\right)=\dfrac{-1}{2}\left(x+y-2 x y-\dfrac{1}{2}\right)$ ) - Montrer que : $\,\,\left(E-\left\{M\left(\dfrac{1}{2}\right)\right\}, \times\right)$ est un groupe commutatif.
- On munit $E$ de la loi de composition interne $T$ définie par :
$$
\forall(x, y) \in \mathbb{R}^2 ;\,\, M(x) T M(y)=M\left(x+y-\dfrac{1}{2}\right)
$$
et on considère l’application $\varphi$ définie de $\mathbb{R}$ vers $E$ par: $\forall x \in \mathbb{R} ;\,\, \varphi(x)=M\left(\dfrac{1-x}{2}\right)$- Montrer que $\varphi$ est un homomorphisme $\operatorname{de}(\mathbb{R},+)$ vers $(E, T)$ et que $\varphi(\mathbb{R})=E$
- En déduire que ( $E, T$ ) est un groupe commutatif.
- Montrer que ( $E, T, \times$ ) est un corps commutatif.
Les Olympiades Nationales de Mathématiques
Durée de réalisation : 3 heures
Date de passation : Vendredi 03 janvier 2025


| a | 2 | 0 | 2 | 4 | b | 2 | 0 | 2 | 5 |
Heureusement, il se rappelle que les chiffres de son code forment un nombre divisible par $99$.
Aider Ahmed à retrouver son code.

Soit $M$ le milieu du segment $[BE]$.
La droite $(AM)$ recoupe $(\Gamma)$ en $C$ et la droite $(EC)$ le recoupe en $D$.
Montrer que les droites $(AD)$ et $(BE)$ sont parallèles.

Dans chacune des cases d’un tableau carré $6 \times 6$, on inscrit l’un des nombres suivants : $0;1;−1$ tels que la valeur absolue de la somme des nombres inscrits dans toutes ses cases soit inférieure ou égale à $12$.
Prouver que le tableau ainsi obtenu contient un carré $3 \times 3$ dont la valeur absolue de la somme de tous les nombres inscrits dans ses cases est inférieure ou égale à $3$.
Epreuve de Mathématiques
Session de Mai 2023
Durée : 2 heures

- Déterminer la nature des séries numériques suivantes :
- $\displaystyle\sum_{n \geq 0} \dfrac{3^n}{n^2 + 1}$
$\quad$(On pourra utiliser le critère de D’Alembert). - $\displaystyle\sum_{n \geq 0} \left( \dfrac{2 \sqrt{e^n} + 1}{3 \sqrt{e^n} + 2} \right)^n $
$\quad$(On pourra utiliser le critère de Cauchy).
- $\displaystyle\sum_{n \geq 0} \dfrac{3^n}{n^2 + 1}$
-
- Montrer que la fonction $ x \mapsto \dfrac{\ln(x+1)}{x+1} $ est décroissante sur l’intervalle $ [2, +\infty[ $.
- En déduire la nature de la série $ \displaystyle\sum_{n \geq 2} (-1)^n \dfrac{\ln(n+1)}{n+1} $.
Barème : $(3pts)=(0.75+0.75)+(0.75+0.75)$

On considère l’équation différentielle suivante : $$(E) : y^{\prime\prime} – 6y^\prime + 5y = -4e^x .$$où $ y $ est une fonction de la variable réelle $ x $, deux fois dérivable sur $ \mathbb{R}$.
- Résoudre l’équation différentielle homogène $ (H)\, :\,\,\, y^{\prime\prime} – 6y’ + 5y = 0 $.
- Vérifier que la fonction $ g $ définie par : $ g(x) = xe^x $ est une solution particulière de $ (E) $.
- Déduire la solution générale de l’équation $ (E) $.
- Soient $ f $ la fonction numérique définie sur $ \mathbb{R} $ par : $ f(x) = (x+2)e^x $ et $ (C_f) $ sa courbe représentative dans un repère orthonormé $ (O, \vec{i}, \vec{j}) $.
- En utilisant une intégration par parties, calculer l’intégrale $ I = \displaystyle\int_0^1 f(x) dx $.
- Déterminer le développement limité de $ f $ à l’ordre 2 au voisinage de 0.
- En déduire l’équation de la tangente $ (T) $ à $ (C_f) $ au point $ A(0, 2) $ et préciser sa position relative par rapport à $ (C_f) $.
Barème : $(7pts)=1+1+1+(1.5+1+1.5)$

On considère l’endomorphisme $f$ de $ \mathbb{R}^2 $ défini par : $ f(x, y) = (5x – 3y, 6x – 4y) $.
Et $ \mathcal{B} = (e_1, e_2) $ la base canonique de $ \mathbb{R}^2 $ (On rappelle que $ e_1 = (1, 0) $ et $ e_2 = (0, 1))$.
- Montrer que la matrice de $f$ dans la base $ \mathcal{B} $ est $ A = \begin{pmatrix} 5 & -3 \\ 6 & -4 \end{pmatrix} $.
- Montrer que le polynôme caractéristique de $A$ est $ P(\lambda) = (\lambda + 1)(\lambda -2) $, puis déduire les valeurs propres $ \lambda_1 $ et $ \lambda_2 $ de la matrice $A$ où $ \lambda_1 < \lambda_2 $.
- Soit $ \mathcal{B}’ = (u_1, u_2) $ où $ u_1 = (1, 2) $ et $ u_2 = (1, 1) $.
- Etablir que $ \mathcal{B}’ $ est une base de $ \mathbb{R}^2 $.
- Vérifier que $ u_1 $ et $ u_2 $ sont des vecteurs propres de $f$ associés respectivement aux valeurs propres $ \lambda_1 $ et $ \lambda_2 $.
- Donner la matrice de passage $P$ de $ \mathcal{B} $ à $ \mathcal{B}’ $ et vérifier que $ P^{-1} = \begin{pmatrix} -1 & 1 \\ 2 & -1 \end{pmatrix} $.
- Déterminer la matrice diagonale $ D $ vérifiant $ A = PDP^{-1} $.
- Calculer $ A^n $ en fonction de $n$ pour tout $n \in \mathbb{N} $.
Barème : $(6pts)=0.5+1+(0.5+1)+1+1+1$

Le tableau suivant présente l’évolution du budget publicitaire et du chiffre d’affaire d’une société au cours des $5$ dernières années:
| Budget publicitaire en millions de dirhams: $x_i $ | $10$ | $12$ | $14$ | $16$ | $18$ |
| Chiffre d’affaire en millions de dirhams: $ y_i $ | $52,5$ | $57,5$ | $70$ | $77,5$ | $92,5$ |
- Déterminer le point moyen $ G $ de cette série statistique.
-
- Calculer le coefficient de corrélation linéaire de cette série statistique.
- Peut-on envisager une relation linéaire entre les deux variables $x$ et $y$ ?
- Montrer que l’équation de la droite de régression linéaire de $y$ en $x$ est : $ y = 5x $.
- Estimer le budget publicitaire lorsque la société aura un chiffre d’affaire de $200$ millions de dirhams.
Barème : $(4pts)=1+(1+0.5)+1+0.5$

On considère la loi $*$ définie sur $\mathbb{R}$ par :
$$ (\forall (x, y) \in \mathbb{R}^2)\, :\,\,\,\, x * y = x + y + \sin(\pi x y) $$
-
- Montrer que la loi $*$ est commutative.
- Montrer que la loi $*$ admet un élément neutre.
- On considère la fonction $f$ définie sur $\mathbb{R}$ par : $f(x) = 1 + x + \sin(\pi x).$
- Montrer que l’équation $f(x) = 0$ admet au moins deux solutions distinctes $-1$ et $\alpha\in\left[-\dfrac{1}{2}, 0\right]$.
- En déduire que l’élément $1$ admet deux inverses distincts dans $(E, *)$.
- Montrer que la loi $*$ n’est pas associative.

Soit $E$ l’ensemble des fonctions deux fois dérivables sur $\mathbb{R}$ qui vérifient :
$$ (\forall x \in \mathbb{R})\, :\,\,\, \varphi^{\prime\prime}(x) = (1 + x^2) \varphi(x) $$
- Montrer que $(E, +, .)$ est un espace vectoriel réel de dimension finie.
- On considère les fonctions $f$ et $g$ définies sur $\mathbb{R}$ par :
$$ f(x) = e^{\frac{x^2}{2}} \quad \text{ et } \quad g(x) = f(x) \int_0^x \dfrac{1}{(f(t))^2} dt $$- Montrer que $f \in E$.
- Montrer que $g \in E$.
- Soit $h\in E$.
- Montrer que la fonction $h = h’f – hf’$ est constante sur $\mathbb{R}$.
- En déduire que la famille $(f,g)$ est génératrice de $E$.
- Montrer que la famille $\{f, g\}$ est une base de $E$, et déterminer $\dim E$.

Pour tout $q \in \mathbb{Q}$, on considère l’ensemble :
$$ E_q = \left\{ M_{(a,b)} = \begin{pmatrix} a & q b \\ b & a \end{pmatrix} \ \big/ \ (a,b) \in \mathbb{R}^2 \right\} $$
- Montrer que $(E, +, \times)$ est un espace vectoriel réel.
- On pose $I = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$ et $U = \begin{pmatrix} 0 & q \\ 1 & 0 \end{pmatrix}$.
Montrer que la famille $\{I, U\}$ est une base de $E$. -
- Montrer que $U^2 = qI$.
- En déduire que $U$ admet un inverse dans $(M_2(\mathbb{R}),\times)$ si et seulement si $q\neq 0$.
- Montrer que pour tout $n \in \mathbb{N}$ : $$U^n = \begin{cases} q^{\frac{n}{2}} I & \text{si } n \text{ est pair} \\ q^{\frac{n-1}{2}} U & \text{si } n \text{ est impair} \end{cases}$$
-
- Montrer que $M_{(a,b)} \times M_{(a’,b’)} = M_{(a a’ + q b b’, a b’ + b a’)}$.
- Montrer que $(E, +, \times)$ est un anneau commutatif et unitaire.
- Montrer que $(E,+,\times)$ est un anneau intègre si et seulement si $q<0$.
- Montrer que $(E, +, \times)$ est un corps si et seulement si $q < 0$. Donner dans ce cas l'inverse de $M_{(a,b)}$.
- On suppose que $q < 0$ et on considère dans $\mathbb{C}$ la loi $*$ définie sur $\mathbb{C}$ par :
$$z * z' = (x x' + q y y') + i (x y' + y x') \,\,\text{ où }\,\, z = x + i y \,\,\text{ et }\,\, z' = x' + i y'$$
- Montrer que $E^*$ est une partie stable de $(E, \times)$, puis en déduire que $\mathbb{C}^*$ est une partie stable de $(\mathbb{C},*)$.
- On considère l’application :
\[\begin{align*}
\varphi\,\,:\,\, &(E^*,\times) \,\,\to \,\,(\mathbb{C}^*,*)\\
&{M_{\left( {a,b} \right)}}\,\,\,\,\,\, \mapsto\,\, a + ib
\end{align*}\]- Montrer que $\varphi$ est un isomorphisme bijectif de $(E^*,\times)$ dans $(\mathbb{C}^*,*)$.
- En déduire que $(E,+,\times)$ est un corps commutatif et déterminer l’inverse de chaque $z$ de $\mathbb{C}^*$.
- Pour tout $n\in\mathbb{N}^*$, calculer : \[{i^{\left( n \right)}} = \underbrace {i*i* \ldots *i}_{n\,\,fois}\]
- Soit $$C(E)=\bigg\{A\in M_2(\mathbb{R})\big/(\forall M\in E): AM=MA \bigg\}$$
- Montrer que $(C(E),+,\times)$ est un anneau commutatif et unitaire.
- Soit $A\in M_2(\mathbb{R})$. Montrer que : \[\bigg[ {\big( {\forall M \in C\left( E \right)} \big)\,\,:\,\,\,\,AM = MA} \bigg] \Leftrightarrow AU = UA\]
- Montrer que : $$\left( {A \in {M_2}\left( R \right)} \right)\,\,:\,\,\,\,\,\,\,AU = UA \Leftrightarrow A \in C\left( E \right)$$
- Déduire l’ensemble $C(E)$.
Durée : 2 heures

On considère les suites $ (I_n)_{n \in \mathbb{N}} $ et $(J_n)_{n \in \mathbb{N}}$ définies par : $$\begin{aligned}
I_n &= \int_0^1 (1-x)^n e^{-x^2} dx\\
J_n &= \int_0^1 x(1-x)^n e^{-x^2} dx
\end{aligned}$$
- On considère la fonction $f$ définie sur $[0,1]$ par : $ f(x) = x e^{-x^2} $.Étudier les variations de la fonction $f$ et dresser son tableau de variations. $(1pt)$
- Montrer que $ (\forall n \in \mathbb{N}),\,\,\, 0 \leq J_n \leq \dfrac{1}{\sqrt{2e}(n+1)}.$ $(1pt)$
- En déduire que la suite $ (J_n) $ est convergente et calculer sa limite. $(0.5pt)$
- Étudier la monotonie de la suite $(I_n)$. $(1pt)$
- Montrer que : $ (\forall n \in \mathbb{N}),\,\,\, I_n = \dfrac{1}{n+1}-\dfrac{2}{n+1} J_{n+1}.$ $(1pt)$
- En déduire $ \lim I_n $ puis $ \lim nI_n$. $(1pt)$

On considère la fonction $F$ définie par : $ F(x) = \displaystyle\int_0^{\ln x} \dfrac{e^t}{(1+t)^2} dt $
- Montrer que l’ensemble de définition de la fonction $ F $ est $ D_F = \left]\dfrac{1}{e}, +\infty\right[$. $(1pt)$
-
- Montrer que $ \left(\forall x \in \left]\dfrac{1}{e}, 1\right]\right),\,\,\, F(x) \leq x \left( 1 – \dfrac{1}{1 + \ln x} \right) $ $(1pt)$
- En déduire : $ \displaystyle\lim_{x \to \left( \frac{1}{e} \right)^+} F(x) $ $(0.5pt)$
-
- Montrer que : $ F(x) = \displaystyle\dfrac{x}{(1 + \ln x)^2} -1 + 2 \int_0^{\ln x} \dfrac{e^t}{(1+t)^3} dt $ $(1pt)$
- En déduire que $(\forall x\ge 1),\,\,\, F(x) \geq \dfrac{x}{(1 + \ln x)^{2}}-1$ et calculer $ \displaystyle\lim_{x \to +\infty} F(x).$ $(1pt)$
-
- Montrer que la fonction $F$ est dérivable sur $\left]\dfrac{1}{e}, +\infty\right[$ et calculer $F'(x)$. $(1pt)$
- En déduire les variations de la fonction $ F $. $(0.5pt)$

On considère l’équation $$(E)\,\,:\,\,\,\, z^2 + az + b = 0\,\,\,\,\text{ où }\,\,\,\,(a, b) \in \mathbb{C}^{*2}.$$Soient, $z$ et $z’$ les solutions de l’équation $(E)$.
Première partie:
- On suppose que $|z| = |z’| = 1$.
-
- Montrer que $|b| = 1$ et $|a| \leq 2$.
- Montrer que $\left(\forall u, v \in \mathbb{C}^*\right)$ : $$|u + v| = |u| + |v| \iff \text{arg}(u) = \text{arg}(v) [2\pi].$$
- Déduire le cas d’égalité dans l’inégalité $|a| \leq 2$.
-
- Montrer que : $$\dfrac{\left(z + z’\right)^2}{zz’}\in \mathbb{R}_+^{*}. $$
- En déduire que : $$\arg(b) \equiv 2 \arg(a) [2\pi].$$
-
- On suppose que : $\left\{ \begin{aligned}
&\left| b \right| = 1\,\,\,\,\,\,,\,\,\,\,\,\left| a \right| \le 2\\
&\arg \left( b \right) \equiv 2\arg \left( a \right)\left[ {2\pi } \right]
\end{aligned} \right.$- Montrer qu’il existe $\alpha$ de $\mathbb{R}_+^*$ tel que $b=\alpha a^2$ et que $\alpha \ge \dfrac{1}{4}$.
- Calculer $z$ et $z’$ les solutions de l’équation $(E)$ en fonction de $a$ et $\alpha$.
- En déduire que $|z| = |z’| = 1$.
- Conclure.
Deuxième partie:
On suppose dans cette partie que $a \in \mathbb{R}$ et $b = 1$.
L’équation $(E)$ devient $(E)\,:\,\, z^2 + az + 1 = 0$.
On Considère $(\Gamma)$ l’ensemble des points $M$ qui sont les images des solutions de l’équation $(E)$ lorsque lorsque $a$ varie dans $\mathbb{R}$.
- Montrer que :
\[M\left( z \right) \in \left( \Gamma \right) \iff \overline {\left( {\frac{{{z^2} + 1}}{z}} \right)} = \frac{{{z^2} + 1}}{z}.\] - Déduire que l’ensemble $(\Gamma)$ est l’union d’un cercle et d’une droite, et déterminer leurs équations.
Durée : 2 heures

Partie I
Déterminer l’ensemble de définition de la fonction : $(1.5pts)$ \[\varphi (x) = \int_1^{{x^2}} {\frac{{dt}}{{\ln t}}} \]
Partie II
On considère la fonction ${F}$ définie sur $[0, +\infty[$ par :
\[\left\{ \begin{array}{l}
F(x) = \displaystyle\int_1^{{x^2}} {\frac{{dt}}{{\ln t}}} ,\quad x \in ]0,1[ \cup ]1, + \infty [\\
F(0) = 0\,\,\, , \,\,\,F(1) = \ln 2
\end{array} \right.\]
-
- Montrer que $F$ est dérivable sur $]1,+\infty[$ et que $ F'(x) = \dfrac{x-1}{x \ln x}.$ (1pt)
- Montrer que $F$ est dérivable sur $]0,1[$ et calculer $F'(x)$. (1pt)
- En déduire les variations de la fonction $f$ sur chacun des intervalles $]1,+\infty$ et $]0,1[$. (1pt)
-
- Montrer que $ (\forall x > 1) \,: \,\,\, F(x) \geq \dfrac{x^2 -x}{2 \ln x}$. (1pt)
- Calculer la limite $\displaystyle\lim_{x \to +\infty} F(x)$ et en déduire la nature de la branche infinie au voisinage de $+\infty$. (1pt)
-
- Montrer que : $(1pt)$ \[\left( {\forall x \in \left] {0,1} \right[} \right)\,\,:\,\,\,\,\,\,\,\frac{{x\left( {x – 1} \right)}}{{2\ln x}} \le F(x) \le \frac{{x\left( {x – 1} \right)}}{{\ln x}}\]
- Montrer que la fonction $F$ est continue à droite en $0$. (0.5pt)
- Montrez que la fonction $F$ est dérivable à droite en $0$ et interpréter le résultat obtenu. (0.75pt)
-
- Montrer que : (0.75pt) $$ \left(\forall x \in \left]0,1\right[ \cup \left]1,+\infty\right[\right) \,:\,\,\, \int_x^{x^2} \dfrac{dt}{t\ln t} = \ln 2$$
- Montrer que : $(1pt)$ $$ (\forall x > 1) \,:\,\, x \ln 2 \leq F(x) \leq x^2 \ln 2 $$
- Trouver un encadrement similaire sur l’intervalle $]0,1[$. (0.5pt)
- En déduire que la fonction $F$ est continue en $1$. (0.75pt)
-
- Montrer que : (0.75pt)\[\left( {\forall x > 1} \right)\left( {\exists {c_x} \in \left] {1,x} \right[} \right):\,\,\,\,\,\,F’\left( x \right) = \frac{{F\left( x \right) – F\left( 1 \right)}}{{x – 1}} = F’\left( {{c_x}} \right)\]
- Montrer que $F$ est dérivable en $1$ et que $F'(1) = 1$. (0.75pt)
-
- Dressez le tableau de variations de la fonction $F$. (0.5pt)
- Tracer $(C_F)$ la courbe représentative de $F.$ (0.5pt)
Partie III:
On considère la suite $(v_n)_{n \in \mathbb{N^*}}$ définie par : $$ v_n = \int_{e^n}^{e^{n+1}} \frac{dt}{\ln t} $$
- Montrer en utilisant un changement de variable que : (0.75pt) \[\left( {\forall n \in \mathbb{N}^*} \right),\quad {v_n} = \int_n^{n + 1} {\frac{{{e^t}}}{t}} dt\]
- On considère la fonction $f$ définie sur $]1, +\infty[$ par : $f(x) = \dfrac{e^x}{x}$.
- Montrer que $f$ est strictement croissante sur $]1, +\infty[$. (0.5pt)
- Montrer que : (0.75pt) \[\left( {\forall n \in\mathbb{N}^*} \right),\quad \frac{{{e^n}}}{n} \le \int_n^{n + 1} f (t)dt \le \frac{{{e^{n + 1}}}}{{n + 1}}\]
- Montrer que l’équation $\dfrac{e^x}{x}=\displaystyle\int_n^{n+1}f(t)dt$ admet une solution unique dans l’intervalle $[n,n+1]$. (0.75pt)
- Montrer que $\displaystyle\lim_{n \to +\infty} \frac{u_n}{n} = 1.$ (0.5pt)
-
- Montrer que $(\forall n\in\mathbb{N}^*)$: (0.75pt) $$ 0 \leq \int_n^{n+1} \frac{e^t}{t^2} dt \leq \frac{1}{n} \int_n^{n+1} \frac{e^t}{t} dt $$
- En déduire que : (0.5pt)\[\displaystyle\mathop {\lim }\limits_{n \to + \infty } \frac{{\displaystyle\int_n^{n + 1} {\frac{{{e^t}}}{{{t^2}}}dt} }}{{\displaystyle\int_n^{n + 1} {\frac{{{e^t}}}{t}dt} }} = 0\]
- Montrer en utilisant une intégration par parties que : (0.75pt) \[\left( {\forall n \in {\mathbb{N}^*}} \right),\quad \int_n^{n + 1} {\frac{{{e^t}}}{t}} dt = \frac{{{e^n}}}{n}\left( {\frac{{ne}}{{n + 1}} – 1} \right) + \int_n^{n + 1} {\frac{{{e^t}}}{{{t^2}}}} dt\]
- En déduire que : (0.75pt) $$ \lim (u_n-n) = \ln(e-1)$$