Équation réduite d’une droite
Toute droite $(\Delta)$ non parallèle à l’axe des ordonnées admet une équation réduite de la forme : $y=mx+p$, où $m$ et $p$ deux nombre réels.
- Le nombre $m$ est le coefficient directeur.
- Le nombre $p$ est l’ordonnée à l’origine.
Exemple :
- Si l’équation est : $y=a$, alors la droite est parallèle à l’axe des abscisses.
- Si l’équation est : $x=b$, alors la droite est parallèle à l’axe des ordonnées.
- Si le point $M(x_M;y_M)$ appartient à la droite $(\Delta)$ signifie que : $y_M=mx_M+p$
Déterminer l’équation réduite d’une droite
- Le coefficient directeur de la droite $(AB)$ est : $m=\dfrac{y_B-y_A}{x_B-x_A}$.
- L’ordonnée à l’origine est : $p=y_A-mx_A$
- Le coefficient directeur est : $$m=\dfrac{y_B-y_A}{x_B-x_A}=\dfrac{1-3}{-1-7}=\dfrac{-2}{-8}=\dfrac{1}{4}$$
- L’ordonnée à l’origine est : $$p=y_A-mx_A=3-\dfrac{1}{4}\times 7=\dfrac{12}{4}-\dfrac{7}{4}=\dfrac{5}{4}$$
Donc l’équation réduite de la droite $(AB)$ est : $$ y=\dfrac{1}{4}x+\dfrac{5}{4}$$
Droites parallèles
$(D): y=mx+p$ et $(D’): y=m’x+p’$
- Si $(D)\parallel(D’)$, alors $m=m’$.
- Si $m=m’$, alors $(D)\parallel(D’)$.
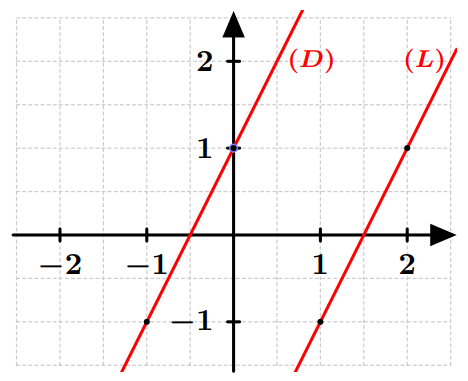
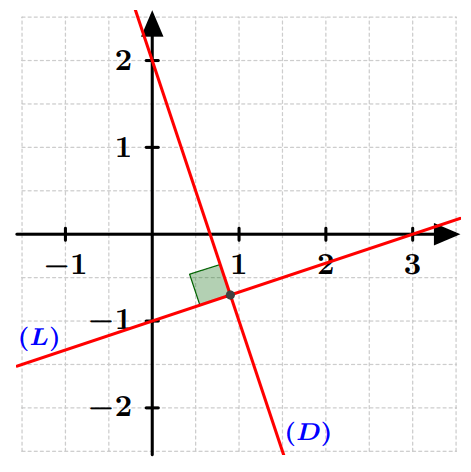
Exemple : Les deux droites $(D)$ et $(L)$ d’équations :
$(D): y=2x+1$ et $(L): y=2x-3$
ont le même coefficient directeur qui $2$, donc : $(D) \parallel (L)$.
Droites perpendiculaires
$(D): y=mx+p$ et $(D’): y=m’x+p’$
- Si $(D)\perp(D’)$, alors $m\times m’=-1$.
- Si $m\times m’=-1$, alors $(D)\perp(D’)$.
Exemple : On considère les deux droites $(D)$ et $(L)$ d’équations :
$(D): y=-3x+2$ et $(L): y=\dfrac{1}{3}x-1$
On a : $-3\times \dfrac{1}{3}=-1$, donc $(D)\perp(L)$.
Premier Semestre
Leçons ciblées : Pythagore, Trigonométrie, Angles inscrits, Triangles semblables.

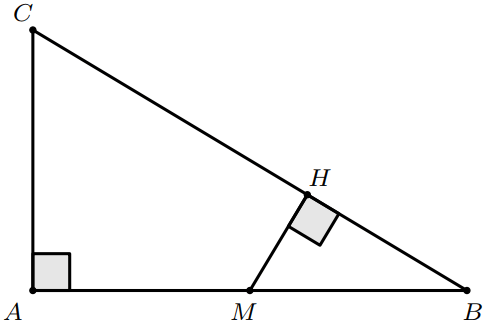
Soit $ABC$ un triangle tels que : $AB=3$, $AC=\sqrt{3}$ et $BC=2\sqrt{3}$
-
- Montrer que $ABC$ est un triangle rectangle en $A$.
- Calculer $\sin \widehat {ABC}$.
- Soit $M$ est le milieu de $[AB]$ et $H$ sa projection orthogonale sur $(BC)$.
- Montrer que : $MH=\dfrac{3}{4}$
- Calculer la distance $HB$.

- Soit $EFG$ un triangle rectangle en $G$ tel que : $\cos {\widehat {GEF}} = \dfrac{{\sqrt 3 }}{3}$ et $EG=\sqrt{3}$
- Calculer $EF$ et $FG$.
- Calculer $\sin\widehat{EFG}$, $\cos\widehat{EFG}$ et $\tan\widehat{EFG}$
- Simplifier les expressions suivantes :
- $U = \sin 30^\circ -\sin 45^\circ -\cos 60^\circ + \tan 60^\circ $
- $V = \tan 15^\circ -\dfrac{1}{{\tan 75^\circ }} -\cos 10^\circ + \sin 80^\circ $
- Soit $\alpha$ la mesure d’un angle aigu.Sachant que $\sin\alpha=\dfrac{1}{7}$, calculer $\cos\alpha$ et $\tan\alpha$.

Soient $A$, $B$, $C$, $D$ quatre points d’un cercle de centre $O$ tels que :
$\widehat{DOC}=100^\circ$ et $\widehat{DAB}=70^\circ$
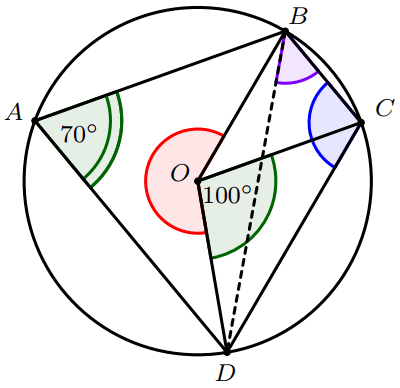
- Calculer la mesure de l’angle $\widehat{DBC}$
- Calculer la mesure de l’angle non convexe $\widehat{BOD}$
- Calculer la mesure de l’angle $\widehat{BCD}$

On considère la figure suivante :
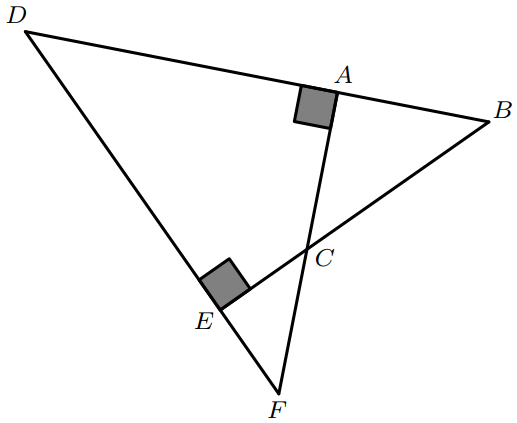
- Montrer que les triangles $BDE$ et $ADF$ sont semblables.
- Montrer que : $BD\times DA=DE\times DF$
- Montrer que les triangles $ACB$ et $ECF$ sont semblables.
Premier Semestre
Leçons ciblées : Théorème de Thalèse, ordre et opérations.

On considère la figure suivante tels que :
$\bullet$ $ABCD$ est un parallélogramme.
$\bullet$ $E$ un point de la droite $(AD)$ tel que : $AE=2$.
$\bullet$ $I$ est le point d’intersection des droites $(AB)$ et $(EC)$
$\bullet$ $M$ un point du segment $[DC]$ tel que : $DM=2,8$
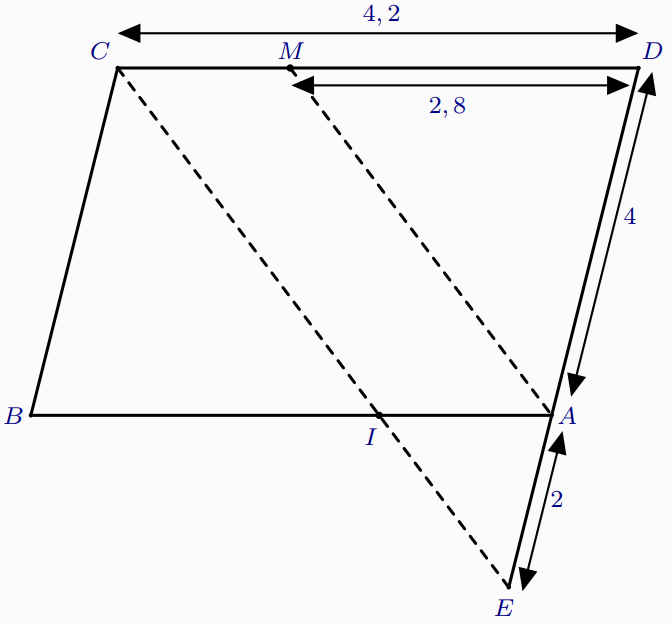
- Montrer que : $AI=1,4$.
(3pts) - Montrer que : $IC=2IE$.
(2pt - Montrer que : $\left( AM\right)\parallel \left( EC\right)$
(3pts) - Montrer que : $3 \times AM =2 \times CE$
(2pts)

-
- Comparer : $\sqrt{19}$ et $3\sqrt{2}$(1.5pts)
- En déduire la simplification de $K$ tel que : $K=\sqrt{\Big( 3\sqrt{2}-\sqrt{19}\Big)^2}+3\sqrt{2}$(1pt)
-
- Comparer : $-3\sqrt{5}$ et $-4\sqrt{3}$(1.5pts)
- En déduire la comparaison des nombres : $\dfrac{1}{2025+3\sqrt{5}}$ et $\dfrac{1}{2025+4\sqrt{3}}$(1pt)

Soient $a$, $b$ et $c$ trois nombres réels tels que :
$1 \le a \le 3$, $-6 \le b \le -2$ et $1 \le \sqrt {5 -c} \le 2$
- Encadrer : $a+b$
(1pt) - Encadrer : $a-b$
(1.5pts) - Montrer que : $0 \le \dfrac{{ab + 18}}{{16}} \le 1$
(1.5pts) - Montrer que : $1 \le c \le 4$
(1pt)
Premier Semestre
Leçons ciblées : Théorème de Thalèse, ordre et opérations.

$AEF$ un triangle tels que :
- $AE=5cm$ et $AF=6cm$ et $EF=7cm$
- $M$ un point de $\left[ {AE} \right]$ tel que $AM = 2cm$
- $C$ un point de $\left[ {AF} \right]$ tel que $\left( {MC} \right)\parallel \left( {EF} \right)$
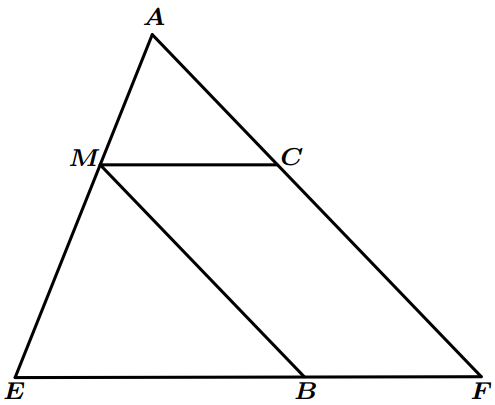
- Calculer $MC$
- Soit $B$ un point de $\left[ {EF} \right]$ tel que : $EB=4,2cm$.
Calculer $EM$ - Montrer que : $\left( {MB} \right)\parallel \left( {AF} \right)$

- Montrer que : $a -b = -\sqrt 5 $
- Déduire la comparaison de $a$ et $b$

- Comparer les nombres suivants :
\begin{array}{lcl}
\mathbf a.\ 5\sqrt{2}~~\text{et}~~3\sqrt{5} &\quad\quad& \mathbf b.\ -\sqrt{30}~~\text{et} ~~-2\sqrt{7}
\end{array} - Déduire la comparaison des nombres suivants :
\begin{array}{lcl}
\mathbf a.\ \dfrac{1}{{2 + 3\sqrt 5 }}~~\text{et}~~\dfrac{1}{{2 + 5\sqrt 2 }} &\quad\quad& \mathbf b.\ \sqrt {3 + \sqrt {30} } ~~\text{et} ~~\sqrt {3 + 2\sqrt 7 }
\end{array} - Comparer les nombres : $\sqrt{2025}+1$ et $\sqrt{2026}$

$1 \le a \le 2~~;~~-3 \le b \le -2~~;~~1 \le \dfrac{1-2c}{3} \le \dfrac{5}{3}$
- Encadrer : $a+b$, $a-b$, $ab+6$ et $b^2-4$
- Montrer que : $ -2 \le c \le -1$

- $A = \sqrt {{{\left( {1 -\sqrt 2 } \right)}^2}} $
- $B = \sqrt {28 +10\sqrt 3 } $
- $C = 2\sqrt {28} + 3\sqrt {63} -13\sqrt 7 $
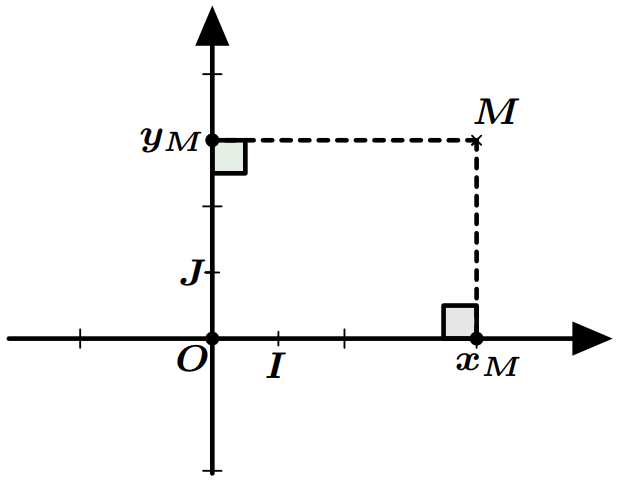
Coordonnées d’un point
- Le couple $(x_M;y_M)$ s’appelle le couple de coordonnées de $M$. On écrit $M(x_M;y_M)$.
- Le nombre $x_M$ s’appelle abscisse du point $M$.
- Le nombre $y_M$ s’appelle ordonnée du point $M$.
- Le point $O$ s’appelle origine du repère.
- La droite $(OI)$ s’appelle l’axe des abscisses.
- La droite $(OJ)$ s’appelle l’axe des ordonnées.
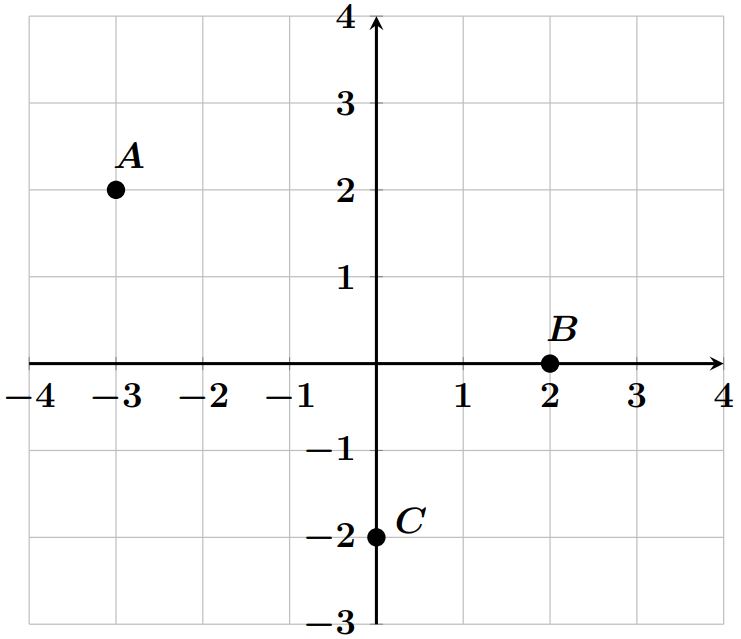
Exemple : Sur la figure suivante, les coordonnées des $A$, $B$ et $C$: $$A(-3;2);\quad B(2;0);\quad C(0;-2)$$
Coordonnées d’un vecteur
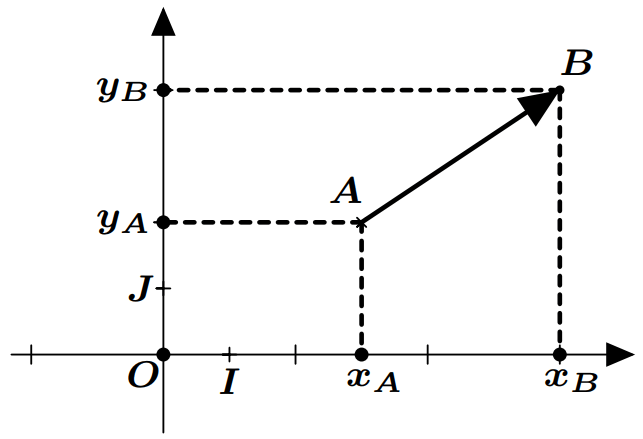
Exemple : On donne : $A(-3;4)$ et $B(-2;-1)$, alors on a : $$\begin{aligned}
& x_B-x_A=-2-(-3)=1\\
& y_B-y_A=-1-4=-5
\end{aligned}$$ Donc : $\boxed{\overrightarrow {AB}(1;-5)}$
Égalité de deux vecteurs
Coordonnées de la somme de deux vecteurs
$$\overrightarrow {AB}+\overrightarrow {CD}(a+c;b+d)$$
Exemple : On donne $\overrightarrow {AB}(-4,-2)$ et $\overrightarrow {CD}(6,-3)$,
donc : $\overrightarrow {AB}+\overrightarrow {CD}(-4+6;-2-3)$,
donc : $\overrightarrow {AB}+\overrightarrow {CD}(2;-5)$
Coordonnées du milieu d’un segment
Si $M$ est le milieu de $[AB]$, alors : $$x_M=\dfrac{x_A+x_B}{2}\quad\text{ et }\quad y_M=\dfrac{y_A+y_B}{2}$$
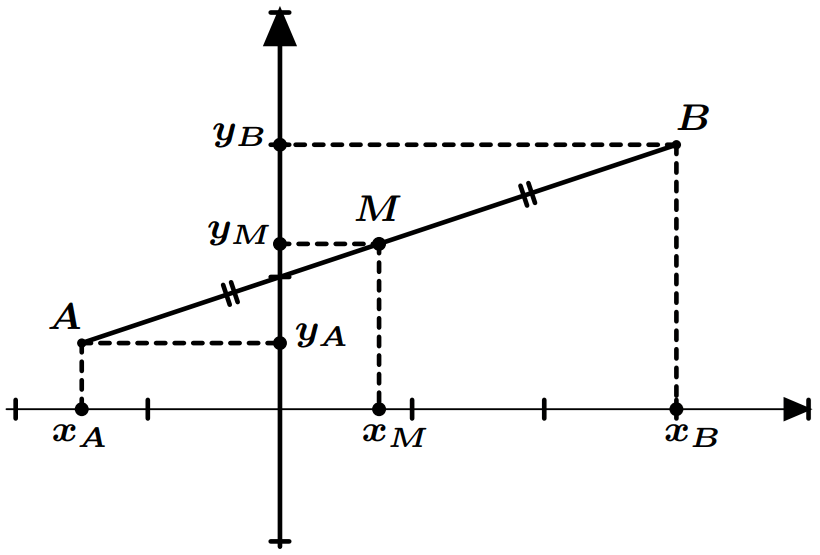
Distance de deux points dans un repère orthonormé
Epreuve de Mathématiques
Juillet 2025
Durée 1h45min

Lors du concours ENSAM Maroc – Mathématiques $2025$, un candidat répond au hasard à l’ensemble des $30$ questions d’un QCM (il ne laisse donc aucune question sans réponse).
Le barème est le suivant : $+2$ points pour une bonne réponse, $-1$ point pour une mauvaise réponse.
Quelle est la probabilité que ce candidat obtienne exactement $25$ points?
\begin{array}{lcl}
\boxed{\mathbf A}\ \,\, \displaystyle\frac{60!}{25!35!}\left(\frac{1}{5}\right)^{25}\left(\frac{4}{5}\right)^{35} &\quad\quad&
\boxed{\mathbf B}\ \,\, \displaystyle\frac{60!}{25!35!}\left(\frac{1}{5}\right)^{35}\left(\frac{4}{5}\right)^{25} &\quad\quad&\\
\boxed{\mathbf C}\ \,\, 0 &\quad\quad&
\boxed{\mathbf D}\ \,\, 1 &\quad\quad&
\boxed{\mathbf E}\ \,\, AR
\end{array}

On définit $h(x)=\displaystyle\int_0^x f(t) d t$. La courbe suivante représente la fonction $f$.
Graphe de $f$ Permi les propositions ci-dessous, laquelle est vraie?
\begin{array}{lcl}
\boxed{\mathbf A}\ \,\, h(6) < h^{\prime}(6) < h^{\prime \prime}(6)&\quad\quad&
\boxed{\mathbf C}\ \,\, h^{\prime}(6) < h(6) < h^{\prime \prime}(6)&\quad\quad&
\boxed{\mathbf E}\ \,\, h^{\prime \prime}(6) < h^{\prime}(6) < h(6)\\
\boxed{\mathbf B}\ \,\, h(6) < h^{\prime \prime}(6) < h^{\prime}(6)&\quad\quad&
\boxed{\mathbf D}\ \,\, h^{\prime \prime}(6) < h(6) < h^{\prime}(6)&\quad\quad&
\end{array}

Soient $f, g$ et $h$ des fonctions définies et dérivables sur $\mathbb{R}$. Elles satisfont les relations suivantes pour tout $x \in \mathbb{R}$ : $f^{\prime}(x)=g(x+1)$ et $g^{\prime}(x)=h(x-1)$. Calculer $f^{\prime \prime}(2 x)$ :
\begin{array}{lcl}
\boxed{\mathbf A}\ \,\, h(2 x+1) &\quad\quad&
\boxed{\mathbf B}\ \,\, 2 h^{\prime}(2 x)&\quad\quad&
\boxed{\mathbf C}\ \,\, h(2 x) &\quad\quad&
\boxed{\mathbf D}\ \,\, 4 h(2 x)&\quad\quad&
\boxed{\mathbf E}\ \,\, AR.&\quad\quad&
\end{array}

Soit $\left(u_n\right)_{n \in \mathbb{N}}$ une suite géométrique de raison $q$. On définit $v_n=\dfrac{u_n}{2}$ pour tout $n \in \mathbb{N}$ et l’on suppose que $\left(v_n\right)$ est arithmétique de raison $\tau$. Déterminet $q+r$.
\begin{array}{lcl}
\boxed{\mathbf A}\ \,\, 0 &\quad\quad&
\boxed{\mathbf B}\ \,\, 1&\quad\quad&
\boxed{\mathbf C}\ \,\, \sqrt{2}&\quad\quad&
\boxed{\mathbf D}\ \,\, \dfrac{1}{2}&\quad\quad&
\boxed{\mathbf E}\ \,\, AR
\end{array}

On considère la suite $\left(a_n\right)_{n \in \mathbb{N}^*}$ définie par $a_{n+1}=\dfrac{1}{a_n}+1, \quad a_1=1$.
Sachant que $a_{100}=\dfrac{k}{m}$, Déterminer la valeur du $98^e$ terme $a_{98}$.
\begin{array}{lcl}
\boxed{\mathbf A}\ \,\, \dfrac{k-m}{2 m-k} &\quad\quad&
\boxed{\mathbf B}\ \,\, \dfrac{k-2 m}{k-m} &\quad\quad&
\boxed{\mathbf C}\ \,\, \dfrac{k-m}{k-2 m} &\quad\quad&
\boxed{\mathbf D}\ \,\, \dfrac{2 m-k}{k-m} &\quad\quad&
\boxed{\mathbf E}\ \,\, AR
\end{array}

Soit la fonction $f(x)=\left(\dfrac{-1+\sin x}{1+\sin x}\right)^2$, et posons $f(x)=x g(x)+1$.
Quelle est la valeur de $\displaystyle\lim _{x \rightarrow 0} g(x)$?
\begin{array}{lcl}
\boxed{\mathbf A}\ \,\, 4 &\quad\quad&
\boxed{\mathbf B}\ \,\, 2 &\quad\quad&
\boxed{\mathbf C}\ \,\, -2 &\quad\quad&
\boxed{\mathbf D}\ \,\, -4 &\quad\quad&
\boxed{\mathbf E}\ \,\, 0 &\quad\quad&
\end{array}

On cherche le plus petit entier naturel à trois chiffres $x$ pour lequel il existe un entier $y$ satisfaisant l’équation $43 x+77 y=273$.
Quelle est la somme des chiffres de cet entier $x$?
\begin{array}{lcl}
\boxed{\mathbf A}\ \,\, 4&\quad\quad&
\boxed{\mathbf B}\ \,\, 5 &\quad\quad&
\boxed{\mathbf C}\ \,\, 8&\quad\quad&
\boxed{\mathbf D}\ \,\, 9&\quad\quad&
\boxed{\mathbf E}\ \,\, 11&\quad\quad&
\end{array}

\begin{array}{lcl}
\boxed{\mathbf A}\ \,\, 5&\quad\quad&
\boxed{\mathbf B}\ \,\, 6&\quad\quad&
\boxed{\mathbf C}\ \,\, 7&\quad\quad&
\boxed{\mathbf D}\ \,\, 8&\quad\quad&
\boxed{\mathbf E}\ \,\, 9
\end{array}

La valeur de l’intégrale est :
\begin{array}{lcl}
\boxed{\mathbf A}\ \,\, \dfrac{\pi}{2}&\quad\quad&
\boxed{\mathbf B}\ \,\, 2 \pi&\quad\quad&
\boxed{\mathbf C}\ \,\, \dfrac{3 \pi}{2}&\quad\quad&
\boxed{\mathbf D}\ \,\, \pi&\quad\quad&
\boxed{\mathbf E}\ \,\, \dfrac{3 \pi}{2}
\end{array}

\begin{array}{lcl}
\boxed{\mathbf A}\ \,\, \text{Non bornée et monotone}\\
\boxed{\mathbf B}\ \,\, \text{Bornée et décroissante}\\
\boxed{\mathbf C}\ \,\, \text{Non bornée et non monotone}\\
\boxed{\mathbf D}\ \,\, \text{Bornée et non monotone}\\
\boxed{\mathbf E}\ \,\, \text{Bornée et croissante}
\end{array}

Sachant que la courbe de $f_n$ rencontre l’axe des abscisses, tandis que celle de $g_n$ ne le rencontre pas.
Quelle est la valeur de $\displaystyle\lim _{n \rightarrow \infty} \frac{b_2}{n^2}$ ?
\begin{array}{lcl}
\boxed{\mathbf A}\ \,\, \dfrac{1}{4} &\quad\quad&
\boxed{\mathbf B}\ \,\, \dfrac{1}{5} &\quad\quad&
\boxed{\mathbf C}\ \,\, \dfrac{2}{5} &\quad\quad&
\boxed{\mathbf D}\ \,\, \dfrac{1}{10} &\quad\quad&
\boxed{\mathbf E}\ \,\, \dfrac{1}{20}
\end{array}

Soient deux fonctions réelles $f$ et $g$ telles que $f(-x)=-f(x)$ et $g(-x)=g(x) \quad(\forall x \in \mathbb{R})$.
On pose $h(x)=f(x) g(x)$. Sachant que $\displaystyle\int_{-3}^3(x+5) h^{\prime}(x) d x=10$, déterminer la valeur de $h(3)$.
\begin{array}{lcl}
\boxed{\mathbf A}\ \,\, 1 &\quad\quad&
\boxed{\mathbf B}\ \,\, 2 &\quad\quad&
\boxed{\mathbf C}\ \,\, 3 &\quad\quad&
\boxed{\mathbf D}\ \,\, 4 &\quad\quad&
\boxed{\mathbf E}\ \,\, 5 &\quad\quad&
\end{array}

Soit $z \in \mathbb{C}$ tel que $\left|\dfrac{z-i}{z+2 i}\right|=1$ et $|z|=\dfrac{5}{2}$.
Quelle est la valeur de $|z+3 i|$ ?
\begin{array}{lcl}
\boxed{\mathbf A}\ \,\, \sqrt{10} &\quad\quad&
\boxed{\mathbf B}\ \,\, \dfrac{7}{2} &\quad\quad&
\boxed{\mathbf C}\ \,\, \dfrac{15}{4} &\quad\quad&
\boxed{\mathbf D}\ \,\, 2 \sqrt{3} &\quad\quad&
\boxed{\mathbf E}\ \,\, AR
\end{array}

Le reste de la division euclidienne de $N$ par 9 est égal à :
\begin{array}{lcl}
\boxed{\mathbf A}\ \,\, 1 &\quad\quad&
\boxed{\mathbf B}\ \,\, 4 &\quad\quad&
\boxed{\mathbf C}\ \,\, 6 &\quad\quad&
\boxed{\mathbf D}\ \,\, 8 &\quad\quad&
\boxed{\mathbf E}\ \,\, AR
\end{array}

On pose $\displaystyle\int_1^2 \frac{x^2}{1+x^4} d x=A$, où $A > 0$ est laissé indéterminé.
En déduire la valeur de $\displaystyle\int_1^2 \frac{x^{-2}}{1+x^4} d x$ en fonction de $A$.
\begin{array}{lcl}
\boxed{\mathbf A}\ \,\, 1-A &\quad\quad&
\boxed{\mathbf A}\ \,\, -A &\quad\quad&
\boxed{\mathbf A}\ \,\, t &\quad\quad&
\boxed{\mathbf A}\ \,\, A-1 &\quad\quad&
\boxed{\mathbf A}\ \,\, \dfrac{1}{2}-A
\end{array}
Epreuve de Mathématiques
Juillet 2025
Durée 1h30min

Le nombre complexe: $$Z=(-1+i \sqrt{3})^{2010}+(-1-i \sqrt{3})^{2010}$$ La valeur de $Z$ est:
\begin{array}{lcl}
\boxed{\mathbf A}\ 2^{2009} &\quad\quad&\boxed{\mathbf B}\ 2 i \sin \left(\dfrac{2 \pi}{3}\right) \exp \left(\dfrac{i 4 \pi}{3}\right)\\
\boxed{\mathbf C}\ 2 \cos \left(\dfrac{4 \pi}{3}\right) \exp \left(\dfrac{i 2 \pi}{3}\right) &\quad\quad&\boxed{\mathbf D}\ 2^{2011}\\
\end{array}

Dans $\mathbb{C}$, on considère l’équation $$z^6=(1-i) \bar{z}\quad\quad (1)$$ On note $z$ une solution non nulle quelconque de de l’équation $(1)$. Alors:
\begin{array}{lcl}
\boxed{\mathbf A}\ |z|=1 &\quad\quad&\boxed{\mathbf B}\ |z|=\sqrt{3}\\
\boxed{\mathbf C}\ |z|=2^{1 / 5} &\quad\quad&\boxed{\mathbf D}\ |z|=2^{1 / 10}\\
\end{array}

Dans $\mathbb{C}$, on considère l’équation $$z^2+z+1=\dfrac{1}{z+1}\quad\quad (2)$$ On note $z_1$ et $z_2$ les solutions non réelles de l’équation $(2)$. On a:
\begin{array}{lcl}
\boxed{\mathbf A}\ \left|z_1\right|=\left|z_2\right| &\quad\quad&\boxed{\mathbf B}\ \left|z_1\right|>\left|z_2\right|\\
\boxed{\mathbf C}\ \left|z_1\right|<\left|z_2\right| &\quad\quad&\boxed{\mathbf D}\ \left|z_1\right|=2\left|z_2\right|\\
\end{array}

On note $S$ l’ensemble des points du plan complexe $M$ dont l’affixe $z$ vérifie $$|z-3|=\dfrac{\sqrt{2}}{2}|z-5|$$ Alors:
\begin{array}{l}
\boxed{\mathbf A}\ S=\emptyset \\
\boxed{\mathbf B}\ S=\mathbb{C}\\
\boxed{\mathbf C}\ S=\text{le cercle de centre } (1,0) \text{ et de rayon } 2 \sqrt{2}\\
\boxed{\mathbf D}\ S=\text{le cercle de centre } (0,1) \text{ et de rayon } \dfrac{1}{2}\\
\end{array}

Dans le plan complexe, on considère les points $A, B, C$ et $D$ d’affixe respective $1,-1, i$ et $-i$. On note $\mathbf{U}$ l’ensemble des nombres complexes de module 1 . Si $M \in \mathbb{U}$, on note $p(M)$ le produit des distances de $M$ aux points $A, B, C, D$ :
$$p(M)=M A \times M B \times M C \times M D$$ On pose $m=\displaystyle\sup _{M \in U} p(M)$. Alors la valeur de $m$ est:
\begin{array}{lcl}
\boxed{\mathbf A}\ m=1 &\quad\quad&\boxed{\mathbf B}\ m=2\\
\boxed{\mathbf C}\ m=3 &\quad\quad&\boxed{\mathbf D}\ m=+\infty\\
\end{array}

Soit a l’entier naturel définit par: $$(2025)^{2025} \equiv a \bmod 7$$ La valeur de $a$ est:
\begin{array}{lcl}
\boxed{\mathbf A}\ a=3 &\quad\quad&\boxed{\mathbf B}\ a=2\\
\boxed{\mathbf C}\ a=5 &\quad\quad&\boxed{\mathbf D}\ a=1\\
\end{array}

Le $\mathrm{PGCD}$ de $3^{123}-5$ et $125$ est:
\begin{array}{lcl}
\boxed{\mathbf A}\ 1 &\quad\quad&\boxed{\mathbf B}\ 5\\
\boxed{\mathbf C}\ 25 &\quad\quad&\boxed{\mathbf D}\ 125\\
\end{array}

On considère la suite $\left(u_n\right)$ définie par: $$u_n=\dfrac{\ln (1+\sqrt{n})}{\ln \left(1+n^3\right)}$$ On note $L=\displaystyle\lim _{n \rightarrow+\infty} u_n$.
\begin{array}{lcl}
\boxed{\mathbf A}\ L=1 &\quad\quad&\boxed{\mathbf B}\ L=\sqrt{3}\\
\boxed{\mathbf C}\ L=\dfrac{1}{6} &\quad\quad&\boxed{\mathbf D}\ L=\dfrac{1}{3}\\
\end{array}

Soit ( $u_n$ ) la suite numérique définie par l’équation $$
\begin{aligned}
u_0 & =1 \\
u_{n+1} & =\dfrac{u_n}{1+2 u_n}, \quad \forall n \geq 0
\end{aligned}
$$ En considérant la suite $v_n=\dfrac{1}{u_n}$, on trouve:
\begin{array}{lcl}
\boxed{\mathbf A}\ \displaystyle\lim _{n \rightarrow+\infty} n u_n=0 &\quad\quad&\boxed{\mathbf B}\ \displaystyle\lim _{n \rightarrow+\infty} n u_n=1\\
\boxed{\mathbf C}\ \displaystyle\lim _{n \rightarrow+\infty} n u_n=\dfrac{1}{2} &\quad\quad&\boxed{\mathbf D}\ \displaystyle\lim _{n \rightarrow+\infty} n u_n=\dfrac{1}{4}\\
\end{array}

Pour $n \in \mathbb{N}^*$, on définit
$$u_n=\sqrt{n+\sqrt{n-1+\sqrt{\cdots+\sqrt{1}}}}$$ La limite $L$ de la suite $(u_n)$ est:
\begin{array}{lcl}
\boxed{\mathbf A}\ L=1 &\quad\quad&\boxed{\mathbf B}\ L=\dfrac{\pi}{2}\\
\boxed{\mathbf C}\ L=+\infty &\quad\quad&\boxed{\mathbf D}\ L=0\\
\end{array}

$$S_n=\sum_{k=1}^{2 n+1} \dfrac{1}{\sqrt{n^2+k}}$$ La limite de $S_n$ est:
\begin{array}{lcl}
\boxed{\mathbf A}\ 0 &\quad\quad&\boxed{\mathbf B}\ \dfrac{1}{2}\\
\boxed{\mathbf C}\ 1 &\quad\quad&\boxed{\mathbf D}\ 2\\
\end{array}

$$
(3+\sqrt{5})^n+(3-\sqrt{5})^n
$$ est un entier pair, la limite
$$
L=\displaystyle\lim _{n \rightarrow+\infty} \cos \left((3+\sqrt{5})^n \pi\right)
$$ vaut:
\begin{array}{lcl}
\boxed{\mathbf A}\ L=0 &\quad\quad&\boxed{\mathbf B}\ L=-1\\
\boxed{\mathbf C}\ L=1 &\quad\quad&\boxed{\mathbf D}\ L=\dfrac{\pi}{4}\\
\end{array}

Soit $a>0$, alors
$$
\displaystyle\lim _{x \rightarrow a^{+}} \dfrac{\sqrt{x}-\sqrt{a}-\sqrt{x-a}}{\sqrt{x^2-a^2}}
$$ est:
\begin{array}{lcl}
\boxed{\mathbf A}\ -\dfrac{1}{\sqrt{2 a}} &\quad\quad&\boxed{\mathbf B}\ -\dfrac{1}{\sqrt{a}}\\
\boxed{\mathbf C}\ \dfrac{1}{\sqrt{a}} &\quad\quad&\boxed{\mathbf D}\ -\dfrac{2}{\sqrt{a}}\\
\end{array}

$$
I_n=\int_0^1 \dfrac{x}{1+x^{2 n}} d x
$$ La limite $L$ de $I_n$ est:
\begin{array}{lcl}
\boxed{\mathbf A}\ L=\dfrac{1}{2} &\quad\quad&\boxed{\mathbf B}\ L=\dfrac{3}{2}\\
\boxed{\mathbf C}\ L=0 &\quad\quad&\boxed{\mathbf D}\ L=\dfrac{\sqrt{2}}{2}\\
\end{array}

La valeur de l’intégrale
$$
I=\int_0^{\sqrt{3}} x^2 \ln \left(x^2+1\right) d x
$$ est:
\begin{array}{lcl}
\boxed{\mathbf A}\ I=\sqrt{3} \ln (2)-\dfrac{\pi}{9} &\quad\quad&\boxed{\mathbf B}\ I=\sqrt{3} \ln (2)+\dfrac{\pi}{9}\\
\boxed{\mathbf C}\ I=2\left(\sqrt{3} \ln (2)-\dfrac{\pi}{9}\right) &\quad\quad&\boxed{\mathbf D}\ I=\sqrt{3} \ln (2)\\
\end{array}

Soit $f$ la fonction définie sur $] 0,+\infty\left[\right.$ par $f(x)=\dfrac{2 \ln (x)}{x\left(1+(\ln (x))^2\right)}$. La primitive de $f$ sur $] 0,+\infty[$ qui s’annule en $1$ est:
\begin{array}{lcl}
\boxed{\mathbf A}\ \ln \left(1+(\ln (x))^2\right) &\quad\quad&\boxed{\mathbf B}\ (\ln (x))^2\\
\boxed{\mathbf C}\ 2 \ln \left(1+(\ln (x))^2\right) &\quad\quad&\boxed{\mathbf D}\ \dfrac{x \ln (x)}{\ln (x)+1}\\
\end{array}

Dans l’espace $\mathbb{R}^3$ rapporté à un repère orthonormé direct ( $O, \vec{i}, \vec{j}, \vec{k}$ ), on considère le plan $(P)$ d’équation $2 x-5 y-6 z+4=0$ et $(S)$ la sphère de centre $\Omega(2 ;-2 ; 3)$ et de rayon 3, alors:
\begin{array}{l}
\boxed{\mathbf A}\ (P) \text{ coupe } (S) \text{ suivant un cercle de rayon } 3 \text{ et de centre }\Omega\\
\boxed{\mathbf B}\ (P) \text{ coupe } (S) \text{ suivant un cercle de rayon } 3 \text{ et de centre le point de coordonnées } (2; 2; 3)\\
\boxed{\mathbf C}\ (P) \text{ est tangent à } (S) \text{ au point de coordonnées } (2 ; 2 ; 3)\\
\boxed{\mathbf D}\ (P) \text{ est tangent à } (S) \text{ au point de coordonnées } (2 ; 0 ;-3)
\end{array}

On jette deux fois de suite une pièce de monnaie non truquée et on note les arrivées de pile et de face. Soit $p$ la probabilité d’avoir deux fois face sachant que le premier jet a donné face.
\begin{array}{lcl}
\boxed{\mathbf A}\ p=\dfrac{1}{2} &\quad\quad&
\boxed{\mathbf B}\ p=\dfrac{1}{3}\\
\boxed{\mathbf C}\ p=\dfrac{1}{4} &\quad\quad&
\boxed{\mathbf D}\ p=\dfrac{3}{4}
\end{array}

Une usine fabrique des composants électroniques et dispose d’une machine pour tester s’ils sont défectueux ou non. Les résultats sont comme suit:
– Si le composant est défectueux: la machine le détecte dans $90 \%$ des cas et dans $10 \%$ des cas elle échoue.
– Si le composant n’est pas défectueux: la machine l’indique correctement dans $99 \%$ des cas et elle échoue dans $1 \%$ des cas.
On tire au hasard un composant dans une large population où l’on sait que $0.1 \%$ des composants sont défectueux, et on note $p$ la probabilité qu’un composant tiré au hasard soit détecté défectueux par la machine.
Alors $p=$
\begin{array}{lcl}
\boxed{\mathbf A}\ p=1.041 \% &\quad\quad&
\boxed{\mathbf B}\ p=1.089 \%\\
\boxed{\mathbf C}\ p=1.025 \% &\quad\quad&
\boxed{\mathbf D}\ p=1 \%
\end{array}

On jette $n$ fois de suite un dé non truqué numéroté de 1 à $6, n \geq 2$, et on note les numéros des faces obtenues. Soit $p_n$ la probabilité d’avoir un nombre inférieur ou égale à 3 dans le second jet sachant que le premier jet a donné la face numéro 2 . Soit $p=\displaystyle\lim _{n \rightarrow+\infty} p_n$.
La valeur de $p$ est:
\begin{array}{lcl}
\boxed{\mathbf A}\ p=\dfrac{1}{2} &\quad\quad&
\boxed{\mathbf B}\ p=\dfrac{1}{3}\\
\boxed{\mathbf C}\ p=\dfrac{1}{6} &\quad\quad&
\boxed{\mathbf D}\ p=0
\end{array}
Égalité de deux vecteurs
- La même direction.
- Le même sens.
- La même longueur (norme).
Exemple :

Figure 1. Egalité de deux vecteurs
Dans les deux cas ci-dessus, les deux vecteurs $\overrightarrow {AB}$ et $\overrightarrow {CD}$ ont :
- La même direction : $\left( {AB\,} \right)\,\parallel \,\,\left( {CD} \right)$.
- Le même sens : $A$ vers $B$.
- La même norme : $AB=CD$.
On écrit : $\overrightarrow {AB} \,\, = \,\,\overrightarrow {CD} $
- $\overrightarrow {AB} \,\, = \,\,\overrightarrow {CD} $ si et seulement si $ABDC$ est un parallélogramme.
- $\overrightarrow {AA} = \overrightarrow {BB} = …… = \,\,\overrightarrow 0 $ est appelé le vecteur nul.
- Si $\overrightarrow {AB} \,\, = \,\,\overrightarrow 0 $ alors $A=B$.
- Le vecteur $\overrightarrow {BA} \,$ est l’opposé du vecteur $\overrightarrow {AB}. \,$
On écrit : $\overrightarrow {AB} = – \overrightarrow {BA} \,$
Somme de deux vecteurs
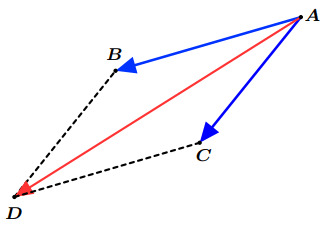
Figure 2: Somme de deux vecteurs
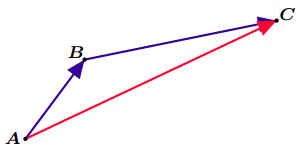
Figure 3: Relation de Chasles
Produit d’un vecteur par un nombre réel
Le vecteur $\overrightarrow {AM}$ est le produit de $\overrightarrow {AB}$ par $\alpha$ signifie que : $\overrightarrow {AM} = \alpha \overrightarrow {AB} $
- Si $\alpha>0$ alors $\overrightarrow {AM}$ et $\overrightarrow {AB}$ ont le même sens, et $AM=\alpha AB$.
- Si $\alpha<0$ alors $\overrightarrow {AM}$ et $\overrightarrow {AB}$ sont de sens contraires, et $AM=-\alpha AB$.
- $\alpha \times \overrightarrow 0 = \overrightarrow 0 $
- $0 \times \overrightarrow {AB} = \overrightarrow 0 $
Exemples :
- Soit $\overrightarrow{AB}$ un vecteur, construire le point $M$ tel que $\overrightarrow {AM} = 4\overrightarrow {AB} $
On a: $\overrightarrow {AM} = 4\overrightarrow {AB} $ signifie que :
$\quad\quad\bullet\quad M \in \left( {AB} \right)$,
$\quad\quad\bullet\quad \overrightarrow {AM}$ et $\overrightarrow {AB}$ ont le même sens,
$\quad\quad\bullet\quad AM=4AB$

Figure 4: Produit d’un vecteurs par un nombre positif
- Soit $\overrightarrow{AB}$ un vecteur, construire le point $N$ tel que $\overrightarrow {AN} = -5\overrightarrow {AB} $
On a: $\overrightarrow {AN} = -\overrightarrow {AB} $ signifie que :
$\quad\quad\bullet\quad N \in \left( {AB} \right)$,
$\quad\quad\bullet\quad\overrightarrow {AN}$ et $\overrightarrow {AB}$ sont de sens contraires,
$\quad\quad\bullet\quad AN=5AB$

Figure 5: Produit d’un vecteurs par un nombre négatif
- $\overrightarrow {AM} = \alpha \overrightarrow {AB} $, alors les points $A$, $M$, $B$ sont alignés.
- Si $\overrightarrow {MN} = \alpha \overrightarrow {AB} $, alors les droites $(MN)$ et $(AB)$ sont parallèles.
Si le point $M$ est le milieu du segment $[AB]$ alors :
$\quad\bullet\quad\overrightarrow {MA} = – \overrightarrow {MB} $
$\quad\bullet\quad\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow 0 $
$\quad\bullet\quad\overrightarrow {AM} = \overrightarrow {MB} = \dfrac{1}{2}\overrightarrow {AB} $
Translation
Image d’un point par une translation
Le point $M’$ est l’image de $M$ par la translation du vecteur $\overrightarrow {AB} $, signifie que : $\overrightarrow {MM’} = \overrightarrow {AB} $
On dit aussi que $M’$ est l’image de $M$ par la translation qui transforme $A$ en $B$.
Exemple:

Figure 6: Image d’un point par une translation
Dans les deux cas ci-dessus, $M’$ est l’image de $M$ par la translation du vecteur $\overrightarrow {AB} $
Si $M’$ et $N’$ sont les images respectives des points $M$ et $N$ par une translation du vecteur $\overrightarrow {u}$, alors : $\overrightarrow {M’N’} =\overrightarrow {MN} $
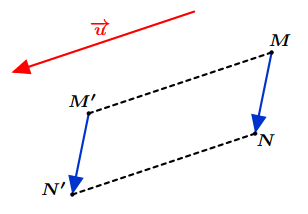
Figure 7: Images de deux points par une translation
Image d’un segment par une translation
L’image du segment $[MN]$ par la translation du vecteur $\overrightarrow {u}$ est le segment $[M’N’]$, et on a : $M’N’=MN$.
On dit que : la translation conserve les longueurs.
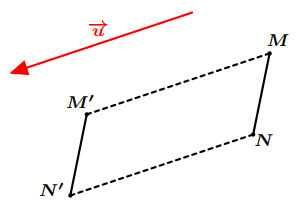
Figure 8: Image d’un segment par une translation
Image d’une droite, demi-droite, points alignés
$\bullet$ L’image de la droite $(MN)$ par la translation du vecteur $\overrightarrow {u}$ est la droite $(M’N’)$, et on a : $(M’N’)\parallel (MN)$
On dit que : la translation conserve l’alignement des points
$\bullet$ L’image de la demi-droite $[MN)$ par la translation du vecteur $\overrightarrow {u}$ est la demi-droite $[M’N’)$.
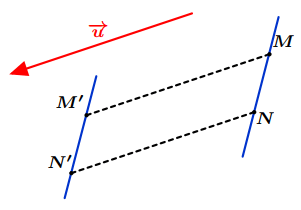
Figure 9: Image d’une droite par une translation
Image d’un angle par une translation
L’image de l’angle $\widehat{AOB}$ par la translation du vecteur $\overrightarrow {u}$ est l’angle $\widehat{A’O’B’}$, et on a : $\widehat{AOB}=\widehat{A’O’B’}$
On dit que: la translation conserve la mesure d’angles.
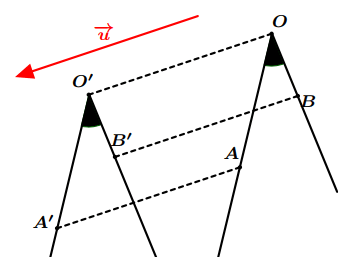
Figure 10: Image d’un angle par une translation
Image d’un cercle par une translation
L’image du cercle $(\mathcal{C})$ de centre $O$ et de rayon $r$ par la translation du vecteur $\overrightarrow {u}$ est le cercle $(\mathcal{C}’)$ de centre $O’$ et de même rayon $r$.
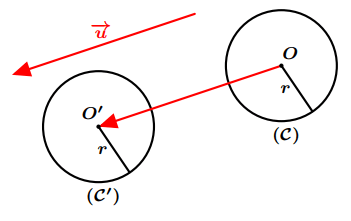
Figure 11: Images d’un cercle par une translation
Équation du premier degré à une inconnue
Exemples : Résolvons les équations suivantes:
- On a : \begin{array}{c}
x\sqrt {27} + 2 = x\sqrt 3 + 1\\
\left( {\sqrt {27} -\sqrt 3 } \right)x = 1\\
\left( {3\sqrt 3 -\sqrt 3 } \right)x = 1\\
2\sqrt 3 x = 1\\
x = \dfrac{1}{{2\sqrt 3 }}\\
x = \dfrac{{\sqrt 3 }}{6}
\end{array}Donc $\dfrac{\sqrt 3}{6}$ est la solution unique de cette équation - On a : \[\begin{array}{c}
\dfrac{{3\left( {x -2} \right)}}{{12}} -\dfrac{{2x}}{{12}} = \dfrac{{12}}{{12}} -\dfrac{{\left( {4 -x} \right)}}{{12}}\\
3x -6 -2x = 12 -4 + x\\
x -6 = 8 + x\\
0x = 14\,\,\left( {\text{impossible}} \right)
\end{array}\]Donc cette équation n’admet pas de solution - On a : \[\begin{array}{c}
\left( {x – 2} \right)\left( {x – 1} \right) – 5 = x\left( {x – 2} \right) – \left( {3 + x} \right)\\
{x^2} – x – 2x + 2 – 5 = {x^2} – 2x – 3 – x\\
{x^2} – 3x – 3 = {x^2} – 3x – 3\\
0x = 0
\end{array}\]ceci est vraie pour tout réel $x$.
Donc tous les nombres réels sont solutions de cette équation.
Équation de la forme $(ax+b)(cs+d)=0$
Les solutions de l’équation $(ax+b)(cx+d)=0$ sont les solutions des deux équations $ax+b=0$ et $cx+d=0$.
\[\begin{array}{c}
\left( {x\sqrt 3 -5} \right)\left( { -x + \sqrt 5 } \right) = 0\\
x\sqrt 3 -5 = 0\,\,\,\,\text{ ou }\,\,\,\, -x + \sqrt 5 = 0\\
x\sqrt 3 = 5\,\,\,\,\text{ ou }\,\,\,\, -x = -\sqrt 5 \\
x = \dfrac{5}{{\sqrt 3 }}\,\,\,\,\text{ ou }\,\,\,\,x = \sqrt 5 \\
x = \dfrac{{5\sqrt 3 }}{3}\,\,\,\,\text{ ou }\,\,\,\,x = \sqrt 5
\end{array}\]Donc cette équation admet deux solutions : $\dfrac{{5\sqrt 3 }}{3}$ et $\sqrt 5 $
Inéquation du premier degré à une inconnue
- On a : \[\begin{array}{l}
4x + 3 < 1\\
4x < 1 – 3\\
4x < – 2\\
x < \dfrac{{ – 2}}{4}\\
x < \dfrac{{ – 1}}{2}
\end{array}\]Donc les solutions de cette inéquation sont les nombres réels strictement inférieurs à $-\dfrac{1}{2}$ - On a :\[\begin{array}{l}
– 2x \le \dfrac{4}{9}\\
x \ge \dfrac{4}{9} \times \dfrac{{ – 1}}{2}\,\,\,\,\left( {car\,\,\,\dfrac{{ – 1}}{2} < 0} \right)\\
x \ge \dfrac{{ – 2}}{9}
\end{array}\]Donc les solutions de cette inéquation sont les nombres réels supérieurs ou égaux à $-\dfrac{2}{9}$
Mise en équation ou inéquation d’un problème
- Choix de l’inconnue.
- Mise en équation ou en inéquation.
- Résolution de l’équation ou de l’inéquation.
- Vérification et interprétation du résultat.

- Développer et réduire les expressions suivantes :
$$\begin{aligned}
A &= {\left( {\sqrt 2 -5\sqrt 3 } \right)^2}\\
B &= {\left( {7 + 3\sqrt 5 } \right)^2}\\
C &= \left( { -2x -\sqrt 7 } \right)\left( { -2x + \sqrt 7 } \right)
\end{aligned}$$ - Factoriser les expressions suivantes :
$$\begin{aligned}
D &= {\left( {x -5} \right)^2} -\left( {2x + 1} \right)\left( {x -5} \right)\\
E &= 49{x^2} -14x + 1 -{\left( {3x -5} \right)^2}
\end{aligned}$$

- Écrire sous forme d’une seule puissance :
\begin{array}{l}
F = {a^2} \times {\left( {{a^3}} \right)^5}\\
G = \dfrac{{{a^{12}}}}{{a \times {a^3}}}\\
H = {27^2} \times {100^3}
\end{array} - Donner l’écriture scientifique de $I$ :
$$I = \dfrac{{7 \times {{10}^{ -12}} \times 36 \times {{10}^5}}}{{21 \times {{10}^{ -4}}}}$$

Calculer et simplifier :
$$\begin{aligned}
J &= 3\sqrt {50} -\sqrt {18} + 2\sqrt {72}\\
K &= {\left( {\dfrac{{\sqrt 2 }}{{\sqrt 2 -1}}} \right)^{ -2}} + {\left( {\dfrac{{\sqrt 2 }}{3}} \right)^{ -2}}\\
L &= {\left( {\sqrt {6 + 2\sqrt 5 } } \right)^{ -1}} \times {\left( {\sqrt {6 -2\sqrt 5 } } \right)^{ -1}}\\
M &= \sqrt {\dfrac{{20 -4\sqrt 3 }}{{45 -9\sqrt 3 }}}\\
N &= {\left( {\sqrt 3 -\sqrt 2 } \right)^{2018}} \times {\left( {\sqrt 3 + \sqrt 2 } \right)^{2018}}\\
O &= \dfrac{{ -4}}{{\sqrt 2 }} + \dfrac{{\sqrt 2 + 1}}{{\sqrt 2 -1}}
\end{aligned}$$

- Écrire sans « $\sqrt{\quad}$ » au dénominateur :
$$\begin{aligned}
P &= \dfrac{{\sqrt 7 + 4}}{{3\sqrt 7 }}\\
Q &= \dfrac{{\sqrt 3 }}{{3\sqrt 3 -2\sqrt 2 }}
\end{aligned}$$ - Montrer que : $\dfrac{1}{{3 + \sqrt 3 }} + \dfrac{1}{{2\sqrt 3 }} = \dfrac{1}{2}$