Epreuve de Mathématiques
Session de rattrapage 2025
Durée : 4 heures

Partie I :
On considère la fonction $f$ définie sur l’intervalle $I = [0; +\infty[$ par :
$$
f(0) = 0 \quad \text{et} \quad f(x) = \frac{x^2 \ln x}{x^2 + 1} \quad \text{si} \quad x \in ]0; +\infty[
$$
Et soit $(C)$ la courbe représentative de la fonction $f$ dans un repère orthonormé $(O, \vec{i}, \vec{j})$.
-
- Étudier la continuité de $f$ à droite en 0
- Étudier la dérivabilité de $f$ à droite en 0 puis interpréter graphiquement le résultat obtenu.
- Calculer $\displaystyle\lim_{x \to +\infty} f(x) $ et $\displaystyle\lim_{x \to +\infty} \dfrac{f(x)}{x}$ puis interpréter graphiquement le résultat obtenu.
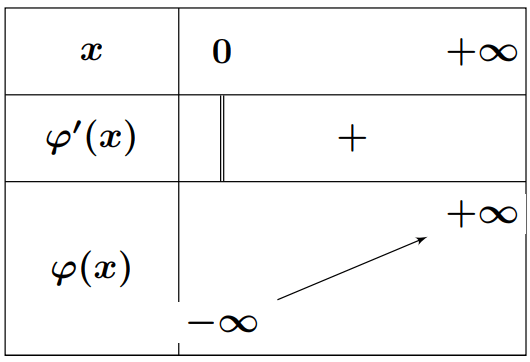
- Soit $\varphi$ la fonction définie sur $]0; +\infty[$ par : $ \varphi(x) = x^2 + 1 + 2 \ln x $
- Dresser le tableau de variations de $\varphi$
- Montrer que l’équation $ \varphi(x) = 0 $ admet une solution unique $\beta$ appartenant à l’intervalle
$ \left[ \dfrac{1}{2} ; \dfrac{1}{\sqrt{3}} \right] $ (On donne $ \ln 2 \simeq 0{,}7 $ et $ \ln 3 \simeq 1{,}1 $) - Montrer que : $ f(\beta) = -\dfrac{\beta^2}{2} $
-
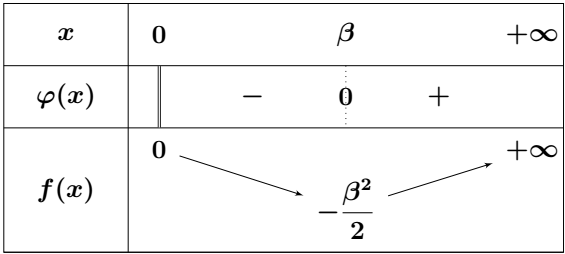
- Montrer que $f$ est dérivable sur $]0; +\infty[$ et que $\left(\forall x \in ]0; +\infty[\right),\quad f'(x) = \dfrac{x \varphi(x)}{(x^2 + 1)^2}$
- Donner le tableau de variations de $f$
- Montrer que $ \dfrac{1}{\beta} $ est l’unique solution de l’équation $ f(x) = \dfrac{1}{2} $ sur $ ]\beta; +\infty[ $
- Montrer que la droite d’équation $ y = \beta x -\dfrac{1}{2} $ est la tangente à la courbe $(C)$ au point d’abscisse $ \dfrac{1}{\beta} $
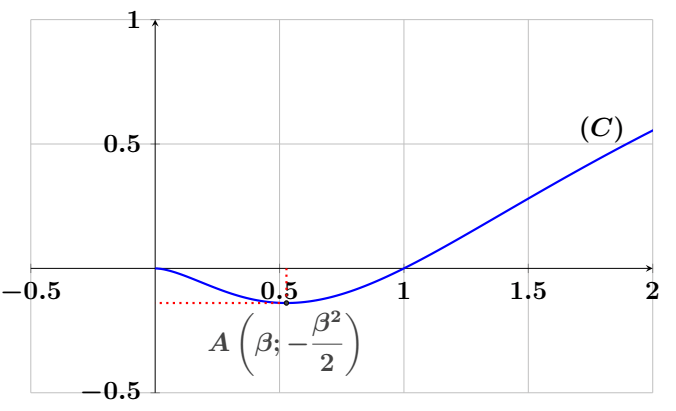
- Représenter graphiquement la courbe $(C)$ dans le repère $(O, \vec{i}, \vec{j})$
(On admet que la courbe $(C)$ possède deux points d’inflexion)
Partie II :
On pose : $ J = \left] \sqrt{3}; 2 \right] \quad \text{et} \quad \alpha = \dfrac{1}{\beta}$
Soit $g$ la fonction définie sur $]0; +\infty[$ par : $ g(x) = \sqrt{e^{1+\frac{1}{x^2}}} $
-
- Étudier les variations de $g$
- Montrer que : $\left(\forall x \in J\right), \quad \sqrt{3} < g(x) < 2$
(On donne $ \sqrt{3} \simeq 1{,}73$, $ e^{1/2} \simeq 1{,}95$ et $ e^{5/6} \simeq 1{,}87$)
-
- En utilisant le résultat de la question I.3-c), montrer que : $ g(\alpha) = \alpha $
- Montrer que : $\left( {\forall x \in J} \right);\quad \left| {g’\left( x \right)} \right| \le \dfrac{2}{{3\sqrt 3 }}$
- En déduire que : $\left( {\forall x \in J} \right);\quad \left| {g\left( x \right) -\alpha } \right| \le \dfrac{2}{{3\sqrt 3 }}\left| {x -\alpha } \right|$
- On considère la suite $(x_n)_{n\in\mathbb{N}}$ définie par : $$x_0=\dfrac{7}{4}\quad\text{et pour tout } n\in\mathbb{N},\quad x_{n+1}=g(x_n)$$
- Montrer que : $\left( {\forall x \in \mathbb{N}} \right);\quad {x_n} \in J$
- Montrer par récurrence que : $\left( {\forall x \in \mathbb{N}} \right);\quad \left| {{x_n} -\alpha } \right| \le {\left( {\dfrac{2}{{3\sqrt 3 }}} \right)^n}\left| {{x_0} -\alpha } \right|$
- En déduire que la suite $(x_n)_{n\in\mathbb{N}}$ converge vers $\alpha$.

On considère la suite numérique $\left(u_n\right)_{n \geq 2}$ définie par: $(\forall n \geq 2) \quad u_n=\dfrac{1}{n} \displaystyle\sum_{k=1}^{n-1} \ln \left(\dfrac{k}{n}\right)$
- Soit $n$ un entier naturel supérieur ou égal à 2.
- Montrer que pour tout entier $k \displaystyle\in\{1,2, \ldots, n-1\}$
et pour tout réel $x \in\left[\dfrac{k}{n} ; \dfrac{k+1}{n}\right]$, on a :
$$\ln \left(\dfrac{k}{n}\right) \leq \ln (x) \leq \ln \left(\dfrac{k+1}{n}\right)$$ - En déduire que : $$\forall k \displaystyle\in\{1,2, \ldots, n-1\};\quad \dfrac{1}{n} \ln \left(\dfrac{k}{n}\right) \leq \displaystyle\int_{\frac{k}{n}}^{\frac{k+1}{n}} \ln (x) d x \leq \dfrac{1}{n} \ln \left(\dfrac{k+1}{n}\right)$$
- Montrer que pour tout entier $k \displaystyle\in\{1,2, \ldots, n-1\}$
-
- Montrer que : $$(\forall n \geq 2);\quad \dfrac{1}{n} \displaystyle\sum_{k=1}^{n-1} \ln \left(\dfrac{k}{n}\right) \leq \displaystyle\int_{\frac{1}{n}}^1 \ln (x) d x \leq \dfrac{1}{n} \sum_{k=2}^n \ln \left(\dfrac{k}{n}\right)$$
- En déduire que : $$(\forall n \geq 2) ;\quad u_n \leq \displaystyle\int_{\frac{1}{n}}^1 \ln (x) d x \leq u_n-\dfrac{1}{n} \ln \left(\dfrac{1}{n}\right)$$
- Montrer que : $$(\forall n \geq 2) ;\quad -1+\dfrac{1}{n} \leq u_n \leq-1+\dfrac{1}{n}-\dfrac{1}{n} \ln \left(\dfrac{1}{n}\right)$$
- Déterminer $\displaystyle\lim _{n \rightarrow+\infty} u_n$

Soit $\theta\in\left[0,\pi\right[$
Partie I:
On considère dans l’ensemble des nombres complexes $\mathbb{C}$ l’équation $(E_\theta)$ d’inconnue $z$
$$(E_\theta):\quad z^2+(1-i)e^{i\theta}z-ie^{i2\theta}=0$$
-
- Vérifier que : $\left(E_\theta\right) \Leftrightarrow\left(2 z+(1-i) e^{i \theta}\right)^2=\left((1+i) e^{i \theta}\right)^2$
- En déduire les deux solutions $z_1$ et $z_2$ de l’équation $\left(E_\theta\right)$ avec $\operatorname{Im}\left(z_1\right) \leq 0$
-
- Montrer que : $\dfrac{z_1+1}{z_2+i}=-\tan \left(\dfrac{\theta}{2}\right)$
- En déduire la forme exponentielle du nombre complexe : $\dfrac{z_1+i z_2}{z_2+i}$
Partie II:
Dans le plan complexe $(\mathcal{P})$ muni d’un repère orthonormé direct $(O, \vec{u}, \vec{v})$, on considère les points $A, B$, et $C$ d’affixes respectives $a=e^{i \theta}, b=(1+i) e^{i \theta}$ et $c=b-a$
Soient $m$ un nombre réel de $] 0 ; 1\left[, R\right.$ la rotation de centre $O$ et d’angle $\dfrac{\pi}{2}$ et le point $Q$ d’affixe $q=m e^{i \theta}$
-
- Déterminer l’affixe $p$ du point $P$ l’image du point $Q$ par la rotation $R$
- Vérifier que : $R(A)=C$
- Soit $H$ le point d’affixe $h=\dfrac{m}{m-i} e^{i \theta}$
- Montrer que : $\dfrac{p-a}{h}=\dfrac{m^2+1}{m} i$ et $\dfrac{h-a}{p-a}=\dfrac{1}{m^2+1}$
- En déduire que $H$ est le projeté orthogonal du point $O$ sur la droite ( $A P$ )
- Montrer que : $\dfrac{b-h}{q-h}=\dfrac{1}{m} i$
- En déduire que les droites $(Q H)$ et $(H B)$ sont perpendiculaires.
- Montrer que les points $A, Q, H$ et $B$ sont cocycliques.

On considère dans $\mathbb{Z} \times \mathbb{Z}$ l’équation $$(E): \quad y=\dfrac{a}{b} x-\dfrac{c}{d}$$ où $a, b, c$ et $d$ sont des entiers naturels non nuls vérifiant : $\quad a \wedge b=c \wedge d=1$
- On suppose que l’équation $(E)$ admet une solution $\left(x_0, y_0\right)$
- Montrer que $d$ divise $b c$
- En déduire que $d$ divise $b$
- On suppose que $d$ divise $b$ et on pose : $b=n d$ où $n$ est un entier naturel non nul.
- Montrer que qu’il existe $(u, v) \in \mathbb{N} \times \mathbb{N}$ tel que : $d n u-a v=1$
- En déduire que l’ensemble des solutions de l’équation $(E)$ est
$$
S=\Big\{(-v c n+b k ;-u c n+a k) / k \in \mathbb{Z}\Big\}
$$ - Résoudre dans $\mathbb{Z}\times \mathbb{Z}$ l’équation $(F): y=\dfrac{3}{2975}x-\dfrac{2}{119}$ (On donne : $2957=119\times 25$)
Epreuve de Mathématiques
Session normale 2025
Durée : 4 heures

On considère la fonction numérique $f$ définie sur $\mathbb{R}$ par :
$$f(x) = \dfrac{e^x}{e^{2x} + e}$$ et soit $(\Gamma)$ sa courbe représentative dans un repère orthogonal $(O; \vec{i}, \vec{j})$.
Partie I :
-
- Montrer que : $\left(\forall x \in \mathbb{R}\right);~~f(1-x) = f(x)$.
- Interpréter graphiquement le résultat obtenu.
- Calculer $\displaystyle\lim_{x \to-\infty} f(x)$ puis en déduire $\displaystyle\lim_{x \to+\infty} f(x)$.
- Interpréter graphiquement les deux résultats obtenus.
-
- Montrer que : $\left(\forall x \in \mathbb{R}\right);~~f'(x) = f(x) \dfrac{1-e^{2x-1}}{1 + e^{2x-1}}$.
- Donner les variations de $f$ puis en déduire que :
$$\left(\forall x \in \mathbb{R}\right);~~0 < f(x) < \dfrac{1}{2}.$$
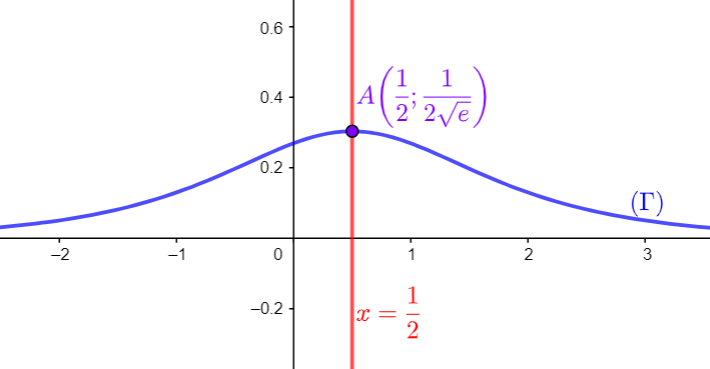
- Représenter graphiquement la courbe $(\Gamma)$.
(On prendra $\left\|\vec{i}\right\|=1\,cm,\, \left\|\vec{j}\right\|=2\,cm,\,\dfrac{1}{2\sqrt{e}} \approx 0.30, \dfrac{1}{1+e} \approx 0.27$).
-
- Montrer que : $\displaystyle\int_{0}^{1/2} f(x)\, dx = \int_{1/2}^1 f(x)\, dx$.
- En déduire que $\displaystyle\int_{0}^{1} f(x)\, dx = 2 \int_{0}^{1/2} f(x)\, dx$.
-
- En effectuant le changement de variable : $t = e^x $, montrer que : $$\int_{0}^{1/2} f(x)\, dx = \int_{1}^{\sqrt{e}} \dfrac{dt}{t^2 + e}.$$
- Montrer que : $$\int_{0}^{1/2} f(x)\, dx = \dfrac{1}{\sqrt{e}} \left(\arctan\left(\sqrt{e}\right)-\dfrac{\pi}{4}\right).$$
- En déduire l’aire, en $cm^2$, du domaine plan délimité par $(\Gamma)$, les droites d’équations respectives : $ x=0$, $x=1$, et $y=0$.
Partie II :
On considère la suite $(u_n)_{n\in\mathbb{N}}$ définie par :
$$u_0 \in \left]0; \dfrac{1}{2}\right[,\, \text{ et }\, \left(\forall n \in \mathbb{N}\right);\,\, u_{n+1} = f(u_n)$$
- En utilisant le résultat de la question I.2-a), montrer que :
$$\left(\forall x \in \mathbb{R}\right);\,\, |f'(x)| \leq f(x)$$ -
- Montrer que :
$$\left(\forall x \in \left[0; \dfrac{1}{2}\right]\right);\,\, 0 \leq f'(x) < \dfrac{1}{2}$$ - Montrer que la fonction $g : x\mapsto g(x)=f(x)-x$ est strictement décroissante sur $\mathbb{R}$.
- En déduire qu’il existe un unique réel $\alpha \in \left]0;\dfrac{1}{2}\right[$ tel que : $f(\alpha)=\alpha$
- Montrer que :
-
- Montrer que : $\left(\forall n \in \mathbb{N}\right); \quad 0 < u_n < \dfrac{1}{2}$
- Montrer que : $\left(\forall n \in \mathbb{N}\right); \quad |u_{n+1}-\alpha| \leq \dfrac{1}{2} |u_n-\alpha|$
- Montrer par récurrence que : $\left(\forall n \in \mathbb{N}\right); \quad |u_n-\alpha| \leq \left( \dfrac{1}{2} \right)^{n+1}$
- En déduire que la suite $(u_n)_{n \in \mathbb{N}}$ converge vers $\alpha$
Partie III :
On considère la suite numérique $(S_n)_{n \in \mathbb{N}}$ définie par : \[\left( {\forall n \in {\mathbb{N}^*}} \right);\quad {S_n} = \frac{1}{{n\left( {n + 1} \right)}}\sum\limits_{k = 1}^{k = n} {\frac{k}{{{e^{\frac{k}{n}}} + {e^{\frac{{n-k}}{n}}}}}} \]
-
- Vérifier que : $\left( {\forall n \in {\mathbb{N}^*}} \right);\quad {S_n} = \dfrac{1}{{n + 1}}\displaystyle\sum\limits_{k = 1}^{k = n} {\dfrac{k}{n}f\left( {\dfrac{k}{n}} \right)} $
- Montrer que: $$\displaystyle\int_0^1 x f(x) \, dx = \int_0^{1/2}f(x) \, dx$$
(On pourra effectuer le changement de variable : $t = 1-x$)
- Montrer que la suite $(S_n)_{n \in \mathbb{N}}$ est convergente et déterminer sa limite.

Soit $\alpha\in\left[0;2\pi\right[$.
On considère dans l’ensemble des nombres complexes $\mathbb{C}$ l’équation $(E_\alpha)$ d’inconnue $z$ : $$(E_\alpha) : \quad z^2-2^\alpha e^{i\alpha}(1 + 2i)z + i2^{2\alpha + 1} e^{i2\alpha} = 0$$
Partie I:
-
- Vérifier que le discriminant de l’équation $(E_\alpha)$ est : $$\Delta_\alpha = \left(2^{\alpha}e^{i\alpha}(1-2i)\right)^2$$
- En déduire les deux solutions $a$ et $b$ de l’équation $(E_\alpha)$ avec $|a| < |b|$
- Vérifier que $\dfrac{b}{a}$ est un imaginaire pur.
Partie II:
Le plan complexe est rapporté à un repère orthonormé direct $(O ; \vec{u}, \vec{v})$.
On note par $M(z)$ le point d’affixe le nombre complexe $z$.
On pose $\dfrac{b}{a}=\lambda i$ avec $\lambda=\operatorname{Im}\left(\dfrac{b}{a}\right)$.
- On considère les points $A(a), B(b)$ et $H(h)$ avec $\dfrac{1}{h}=\dfrac{1}{a}+\dfrac{1}{b}$.
- Montrer que $: \dfrac{h}{b-a}=-\left(\dfrac{\lambda}{\lambda^2+1}\right) i$ puis en déduire que les droites $(O H) \operatorname{et}(A B)$ sont perpendiculaires.
- Montrer que : $\dfrac{h-a}{b-a}=\dfrac{1}{\lambda^2+1}$ puis en déduire que les points $H, A$ et $B$ sont alignés.
- Soient $I(m)$ le milieu du segment $[O H]$ et $J(n)$ le milieu du segment $[H B]$.
- Montrer que : $\dfrac{n}{m-a}=-\lambda i$.
- En déduire que les droites $(O J)$ et $(A I)$ sont perpendiculaires et que $O J=|\lambda| A I$.
- Soit $K$ le point d’intersection des droites ( $O J$ ) et ( $A I$ )Montrer que les points $K, I, H$ et $J$ sont cocycliques.
- Montrer que les droites $(I J)$ et $(O A)$ sont perpendiculaires.

Soient $p$ un nombre premier impair et $a$ un entier premier avec $p$.
- Montrer que : $\,\,a^{\frac{p-1}{2}} \equiv 1[p]$ ou $a^{\frac{p-1}{2}} \equiv-1[p]$.
- On considère dans $\mathbb{Z}$ l’équation : $\,\,a x^2 \equiv 1[p]$. Soit $x_0$ une solution de cette équation.
- Montrer que : $\,\,x_0{ }^{p-1} \equiv 1[p]$.
- En déduire que : $\,\,a^{\frac{p-1}{2}} \equiv 1[p]$.
- Soit $n$ un entier naturel non nul.
- Montrer que si $p$ divise $2^{2 n+1}-1$ alors $2^{\frac{p-1}{2}} \equiv 1[p]$.
- En déduire que l’équation $(E):\,\, 11 x+\left(2^{2 n+1}-1\right) y=1$ admet au moins une solution dans $\mathbb{Z}^2$.
- On considère dans $\mathbb{Z}$ l’équation $(F):\,\, x^2+5 x+2 \equiv 0 \quad[11]$.
- Montrer que : $\,\,(F) \Leftrightarrow 2(2 x+5)^2 \equiv 1[11]$.
- En déduire que l’équation $(F)$ n’admet pas de solution dans $\mathbb{Z}$.

On rappelle que $\left(M_3(\mathbb{R}),+, \times\right)$ est un anneau unitaire et non commutatif de zéro la matrice $O=\left(\begin{array}{lll}0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{array}\right)$ et d’unité la matrice $I=\left(\begin{array}{lll}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right)$, et que $\left(M_3(\mathbb{R}),+,.\right)$ est un espace vectoriel réel.
Soient la matrice $A=\left(\begin{array}{ccc}-1 & -1 & 0 \\ -1 & -1 & 0 \\ -1 & 1 & -2\end{array}\right)$ et l’ensemble $E=\{M(x)=I+x A / x \in \mathbb{R}\}$
-
- Vérifier que : $\,\,A^2=-2 A$
- En déduire que : $\,\,\forall(x, y) \in \mathbb{R}^2 ;\,\, M(x) \times M(y)=M(x+y-2 x y)$
-
- Calculer : $\,\,M\left(\dfrac{1}{2}\right) \times\left(\begin{array}{lll}0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1\end{array}\right)$
- En déduire que la matrice $M\left(\dfrac{1}{2}\right)$ n’est pas inversible dans $\left(M_3(\mathbb{R}), \times\right)$
- Montrer que : $E-\left\{M\left(\dfrac{1}{2}\right)\right\}$ est stable pour la multiplication dans $M_3(\mathbb{R})$
(on pourra utiliser l’identité : $\left(x-\dfrac{1}{2}\right)\left(y-\dfrac{1}{2}\right)=\dfrac{-1}{2}\left(x+y-2 x y-\dfrac{1}{2}\right)$ ) - Montrer que : $\,\,\left(E-\left\{M\left(\dfrac{1}{2}\right)\right\}, \times\right)$ est un groupe commutatif.
- On munit $E$ de la loi de composition interne $T$ définie par :
$$
\forall(x, y) \in \mathbb{R}^2 ;\,\, M(x) T M(y)=M\left(x+y-\dfrac{1}{2}\right)
$$
et on considère l’application $\varphi$ définie de $\mathbb{R}$ vers $E$ par: $\forall x \in \mathbb{R} ;\,\, \varphi(x)=M\left(\dfrac{1-x}{2}\right)$- Montrer que $\varphi$ est un homomorphisme $\operatorname{de}(\mathbb{R},+)$ vers $(E, T)$ et que $\varphi(\mathbb{R})=E$
- En déduire que ( $E, T$ ) est un groupe commutatif.
- Montrer que ( $E, T, \times$ ) est un corps commutatif.
Les Olympiades Nationales de Mathématiques
Durée de réalisation : 3 heures
Date de passation : Vendredi 03 janvier 2025


| a | 2 | 0 | 2 | 4 | b | 2 | 0 | 2 | 5 |
Heureusement, il se rappelle que les chiffres de son code forment un nombre divisible par $99$.
Aider Ahmed à retrouver son code.

Soit $M$ le milieu du segment $[BE]$.
La droite $(AM)$ recoupe $(\Gamma)$ en $C$ et la droite $(EC)$ le recoupe en $D$.
Montrer que les droites $(AD)$ et $(BE)$ sont parallèles.

Dans chacune des cases d’un tableau carré $6 \times 6$, on inscrit l’un des nombres suivants : $0;1;−1$ tels que la valeur absolue de la somme des nombres inscrits dans toutes ses cases soit inférieure ou égale à $12$.
Prouver que le tableau ainsi obtenu contient un carré $3 \times 3$ dont la valeur absolue de la somme de tous les nombres inscrits dans ses cases est inférieure ou égale à $3$.
Epreuve de Mathématiques
Session de Mai 2023
Durée : 2 heures

- Déterminer la nature des séries numériques suivantes :
- $\displaystyle\sum_{n \geq 0} \dfrac{3^n}{n^2 + 1}$
$\quad$(On pourra utiliser le critère de D’Alembert). - $\displaystyle\sum_{n \geq 0} \left( \dfrac{2 \sqrt{e^n} + 1}{3 \sqrt{e^n} + 2} \right)^n $
$\quad$(On pourra utiliser le critère de Cauchy).
- $\displaystyle\sum_{n \geq 0} \dfrac{3^n}{n^2 + 1}$
-
- Montrer que la fonction $ x \mapsto \dfrac{\ln(x+1)}{x+1} $ est décroissante sur l’intervalle $ [2, +\infty[ $.
- En déduire la nature de la série $ \displaystyle\sum_{n \geq 2} (-1)^n \dfrac{\ln(n+1)}{n+1} $.
Barème : $(3pts)=(0.75+0.75)+(0.75+0.75)$

On considère l’équation différentielle suivante : $$(E) : y^{\prime\prime} – 6y^\prime + 5y = -4e^x .$$où $ y $ est une fonction de la variable réelle $ x $, deux fois dérivable sur $ \mathbb{R}$.
- Résoudre l’équation différentielle homogène $ (H)\, :\,\,\, y^{\prime\prime} – 6y’ + 5y = 0 $.
- Vérifier que la fonction $ g $ définie par : $ g(x) = xe^x $ est une solution particulière de $ (E) $.
- Déduire la solution générale de l’équation $ (E) $.
- Soient $ f $ la fonction numérique définie sur $ \mathbb{R} $ par : $ f(x) = (x+2)e^x $ et $ (C_f) $ sa courbe représentative dans un repère orthonormé $ (O, \vec{i}, \vec{j}) $.
- En utilisant une intégration par parties, calculer l’intégrale $ I = \displaystyle\int_0^1 f(x) dx $.
- Déterminer le développement limité de $ f $ à l’ordre 2 au voisinage de 0.
- En déduire l’équation de la tangente $ (T) $ à $ (C_f) $ au point $ A(0, 2) $ et préciser sa position relative par rapport à $ (C_f) $.
Barème : $(7pts)=1+1+1+(1.5+1+1.5)$

On considère l’endomorphisme $f$ de $ \mathbb{R}^2 $ défini par : $ f(x, y) = (5x – 3y, 6x – 4y) $.
Et $ \mathcal{B} = (e_1, e_2) $ la base canonique de $ \mathbb{R}^2 $ (On rappelle que $ e_1 = (1, 0) $ et $ e_2 = (0, 1))$.
- Montrer que la matrice de $f$ dans la base $ \mathcal{B} $ est $ A = \begin{pmatrix} 5 & -3 \\ 6 & -4 \end{pmatrix} $.
- Montrer que le polynôme caractéristique de $A$ est $ P(\lambda) = (\lambda + 1)(\lambda -2) $, puis déduire les valeurs propres $ \lambda_1 $ et $ \lambda_2 $ de la matrice $A$ où $ \lambda_1 < \lambda_2 $.
- Soit $ \mathcal{B}’ = (u_1, u_2) $ où $ u_1 = (1, 2) $ et $ u_2 = (1, 1) $.
- Etablir que $ \mathcal{B}’ $ est une base de $ \mathbb{R}^2 $.
- Vérifier que $ u_1 $ et $ u_2 $ sont des vecteurs propres de $f$ associés respectivement aux valeurs propres $ \lambda_1 $ et $ \lambda_2 $.
- Donner la matrice de passage $P$ de $ \mathcal{B} $ à $ \mathcal{B}’ $ et vérifier que $ P^{-1} = \begin{pmatrix} -1 & 1 \\ 2 & -1 \end{pmatrix} $.
- Déterminer la matrice diagonale $ D $ vérifiant $ A = PDP^{-1} $.
- Calculer $ A^n $ en fonction de $n$ pour tout $n \in \mathbb{N} $.
Barème : $(6pts)=0.5+1+(0.5+1)+1+1+1$

Le tableau suivant présente l’évolution du budget publicitaire et du chiffre d’affaire d’une société au cours des $5$ dernières années:
| Budget publicitaire en millions de dirhams: $x_i $ | $10$ | $12$ | $14$ | $16$ | $18$ |
| Chiffre d’affaire en millions de dirhams: $ y_i $ | $52,5$ | $57,5$ | $70$ | $77,5$ | $92,5$ |
- Déterminer le point moyen $ G $ de cette série statistique.
-
- Calculer le coefficient de corrélation linéaire de cette série statistique.
- Peut-on envisager une relation linéaire entre les deux variables $x$ et $y$ ?
- Montrer que l’équation de la droite de régression linéaire de $y$ en $x$ est : $ y = 5x $.
- Estimer le budget publicitaire lorsque la société aura un chiffre d’affaire de $200$ millions de dirhams.
Barème : $(4pts)=1+(1+0.5)+1+0.5$

On considère la loi $*$ définie sur $\mathbb{R}$ par :
$$ (\forall (x, y) \in \mathbb{R}^2)\, :\,\,\,\, x * y = x + y + \sin(\pi x y) $$
-
- Montrer que la loi $*$ est commutative.
- Montrer que la loi $*$ admet un élément neutre.
- On considère la fonction $f$ définie sur $\mathbb{R}$ par : $f(x) = 1 + x + \sin(\pi x).$
- Montrer que l’équation $f(x) = 0$ admet au moins deux solutions distinctes $-1$ et $\alpha\in\left[-\dfrac{1}{2}, 0\right]$.
- En déduire que l’élément $1$ admet deux inverses distincts dans $(E, *)$.
- Montrer que la loi $*$ n’est pas associative.

Soit $E$ l’ensemble des fonctions deux fois dérivables sur $\mathbb{R}$ qui vérifient :
$$ (\forall x \in \mathbb{R})\, :\,\,\, \varphi^{\prime\prime}(x) = (1 + x^2) \varphi(x) $$
- Montrer que $(E, +, .)$ est un espace vectoriel réel de dimension finie.
- On considère les fonctions $f$ et $g$ définies sur $\mathbb{R}$ par :
$$ f(x) = e^{\frac{x^2}{2}} \quad \text{ et } \quad g(x) = f(x) \int_0^x \dfrac{1}{(f(t))^2} dt $$- Montrer que $f \in E$.
- Montrer que $g \in E$.
- Soit $h\in E$.
- Montrer que la fonction $h = h’f – hf’$ est constante sur $\mathbb{R}$.
- En déduire que la famille $(f,g)$ est génératrice de $E$.
- Montrer que la famille $\{f, g\}$ est une base de $E$, et déterminer $\dim E$.

Pour tout $q \in \mathbb{Q}$, on considère l’ensemble :
$$ E_q = \left\{ M_{(a,b)} = \begin{pmatrix} a & q b \\ b & a \end{pmatrix} \ \big/ \ (a,b) \in \mathbb{R}^2 \right\} $$
- Montrer que $(E, +, \times)$ est un espace vectoriel réel.
- On pose $I = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$ et $U = \begin{pmatrix} 0 & q \\ 1 & 0 \end{pmatrix}$.
Montrer que la famille $\{I, U\}$ est une base de $E$. -
- Montrer que $U^2 = qI$.
- En déduire que $U$ admet un inverse dans $(M_2(\mathbb{R}),\times)$ si et seulement si $q\neq 0$.
- Montrer que pour tout $n \in \mathbb{N}$ : $$U^n = \begin{cases} q^{\frac{n}{2}} I & \text{si } n \text{ est pair} \\ q^{\frac{n-1}{2}} U & \text{si } n \text{ est impair} \end{cases}$$
-
- Montrer que $M_{(a,b)} \times M_{(a’,b’)} = M_{(a a’ + q b b’, a b’ + b a’)}$.
- Montrer que $(E, +, \times)$ est un anneau commutatif et unitaire.
- Montrer que $(E,+,\times)$ est un anneau intègre si et seulement si $q<0$.
- Montrer que $(E, +, \times)$ est un corps si et seulement si $q < 0$. Donner dans ce cas l'inverse de $M_{(a,b)}$.
- On suppose que $q < 0$ et on considère dans $\mathbb{C}$ la loi $*$ définie sur $\mathbb{C}$ par :
$$z * z' = (x x' + q y y') + i (x y' + y x') \,\,\text{ où }\,\, z = x + i y \,\,\text{ et }\,\, z' = x' + i y'$$
- Montrer que $E^*$ est une partie stable de $(E, \times)$, puis en déduire que $\mathbb{C}^*$ est une partie stable de $(\mathbb{C},*)$.
- On considère l’application :
\[\begin{align*}
\varphi\,\,:\,\, &(E^*,\times) \,\,\to \,\,(\mathbb{C}^*,*)\\
&{M_{\left( {a,b} \right)}}\,\,\,\,\,\, \mapsto\,\, a + ib
\end{align*}\]- Montrer que $\varphi$ est un isomorphisme bijectif de $(E^*,\times)$ dans $(\mathbb{C}^*,*)$.
- En déduire que $(E,+,\times)$ est un corps commutatif et déterminer l’inverse de chaque $z$ de $\mathbb{C}^*$.
- Pour tout $n\in\mathbb{N}^*$, calculer : \[{i^{\left( n \right)}} = \underbrace {i*i* \ldots *i}_{n\,\,fois}\]
- Soit $$C(E)=\bigg\{A\in M_2(\mathbb{R})\big/(\forall M\in E): AM=MA \bigg\}$$
- Montrer que $(C(E),+,\times)$ est un anneau commutatif et unitaire.
- Soit $A\in M_2(\mathbb{R})$. Montrer que : \[\bigg[ {\big( {\forall M \in C\left( E \right)} \big)\,\,:\,\,\,\,AM = MA} \bigg] \Leftrightarrow AU = UA\]
- Montrer que : $$\left( {A \in {M_2}\left( R \right)} \right)\,\,:\,\,\,\,\,\,\,AU = UA \Leftrightarrow A \in C\left( E \right)$$
- Déduire l’ensemble $C(E)$.
Durée : 2 heures

On considère les suites $ (I_n)_{n \in \mathbb{N}} $ et $(J_n)_{n \in \mathbb{N}}$ définies par : $$\begin{aligned}
I_n &= \int_0^1 (1-x)^n e^{-x^2} dx\\
J_n &= \int_0^1 x(1-x)^n e^{-x^2} dx
\end{aligned}$$
- On considère la fonction $f$ définie sur $[0,1]$ par : $ f(x) = x e^{-x^2} $.Étudier les variations de la fonction $f$ et dresser son tableau de variations. $(1pt)$
- Montrer que $ (\forall n \in \mathbb{N}),\,\,\, 0 \leq J_n \leq \dfrac{1}{\sqrt{2e}(n+1)}.$ $(1pt)$
- En déduire que la suite $ (J_n) $ est convergente et calculer sa limite. $(0.5pt)$
- Étudier la monotonie de la suite $(I_n)$. $(1pt)$
- Montrer que : $ (\forall n \in \mathbb{N}),\,\,\, I_n = \dfrac{1}{n+1}-\dfrac{2}{n+1} J_{n+1}.$ $(1pt)$
- En déduire $ \lim I_n $ puis $ \lim nI_n$. $(1pt)$

On considère la fonction $F$ définie par : $ F(x) = \displaystyle\int_0^{\ln x} \dfrac{e^t}{(1+t)^2} dt $
- Montrer que l’ensemble de définition de la fonction $ F $ est $ D_F = \left]\dfrac{1}{e}, +\infty\right[$. $(1pt)$
-
- Montrer que $ \left(\forall x \in \left]\dfrac{1}{e}, 1\right]\right),\,\,\, F(x) \leq x \left( 1 – \dfrac{1}{1 + \ln x} \right) $ $(1pt)$
- En déduire : $ \displaystyle\lim_{x \to \left( \frac{1}{e} \right)^+} F(x) $ $(0.5pt)$
-
- Montrer que : $ F(x) = \displaystyle\dfrac{x}{(1 + \ln x)^2} -1 + 2 \int_0^{\ln x} \dfrac{e^t}{(1+t)^3} dt $ $(1pt)$
- En déduire que $(\forall x\ge 1),\,\,\, F(x) \geq \dfrac{x}{(1 + \ln x)^{2}}-1$ et calculer $ \displaystyle\lim_{x \to +\infty} F(x).$ $(1pt)$
-
- Montrer que la fonction $F$ est dérivable sur $\left]\dfrac{1}{e}, +\infty\right[$ et calculer $F'(x)$. $(1pt)$
- En déduire les variations de la fonction $ F $. $(0.5pt)$

On considère l’équation $$(E)\,\,:\,\,\,\, z^2 + az + b = 0\,\,\,\,\text{ où }\,\,\,\,(a, b) \in \mathbb{C}^{*2}.$$Soient, $z$ et $z’$ les solutions de l’équation $(E)$.
Première partie:
- On suppose que $|z| = |z’| = 1$.
-
- Montrer que $|b| = 1$ et $|a| \leq 2$.
- Montrer que $\left(\forall u, v \in \mathbb{C}^*\right)$ : $$|u + v| = |u| + |v| \iff \text{arg}(u) = \text{arg}(v) [2\pi].$$
- Déduire le cas d’égalité dans l’inégalité $|a| \leq 2$.
-
- Montrer que : $$\dfrac{\left(z + z’\right)^2}{zz’}\in \mathbb{R}_+^{*}. $$
- En déduire que : $$\arg(b) \equiv 2 \arg(a) [2\pi].$$
-
- On suppose que : $\left\{ \begin{aligned}
&\left| b \right| = 1\,\,\,\,\,\,,\,\,\,\,\,\left| a \right| \le 2\\
&\arg \left( b \right) \equiv 2\arg \left( a \right)\left[ {2\pi } \right]
\end{aligned} \right.$- Montrer qu’il existe $\alpha$ de $\mathbb{R}_+^*$ tel que $b=\alpha a^2$ et que $\alpha \ge \dfrac{1}{4}$.
- Calculer $z$ et $z’$ les solutions de l’équation $(E)$ en fonction de $a$ et $\alpha$.
- En déduire que $|z| = |z’| = 1$.
- Conclure.
Deuxième partie:
On suppose dans cette partie que $a \in \mathbb{R}$ et $b = 1$.
L’équation $(E)$ devient $(E)\,:\,\, z^2 + az + 1 = 0$.
On Considère $(\Gamma)$ l’ensemble des points $M$ qui sont les images des solutions de l’équation $(E)$ lorsque lorsque $a$ varie dans $\mathbb{R}$.
- Montrer que :
\[M\left( z \right) \in \left( \Gamma \right) \iff \overline {\left( {\frac{{{z^2} + 1}}{z}} \right)} = \frac{{{z^2} + 1}}{z}.\] - Déduire que l’ensemble $(\Gamma)$ est l’union d’un cercle et d’une droite, et déterminer leurs équations.
Durée : 2 heures

Partie I
Déterminer l’ensemble de définition de la fonction : $(1.5pts)$ \[\varphi (x) = \int_1^{{x^2}} {\frac{{dt}}{{\ln t}}} \]
Partie II
On considère la fonction ${F}$ définie sur $[0, +\infty[$ par :
\[\left\{ \begin{array}{l}
F(x) = \displaystyle\int_1^{{x^2}} {\frac{{dt}}{{\ln t}}} ,\quad x \in ]0,1[ \cup ]1, + \infty [\\
F(0) = 0\,\,\, , \,\,\,F(1) = \ln 2
\end{array} \right.\]
-
- Montrer que $F$ est dérivable sur $]1,+\infty[$ et que $ F'(x) = \dfrac{x-1}{x \ln x}.$ (1pt)
- Montrer que $F$ est dérivable sur $]0,1[$ et calculer $F'(x)$. (1pt)
- En déduire les variations de la fonction $f$ sur chacun des intervalles $]1,+\infty$ et $]0,1[$. (1pt)
-
- Montrer que $ (\forall x > 1) \,: \,\,\, F(x) \geq \dfrac{x^2 -x}{2 \ln x}$. (1pt)
- Calculer la limite $\displaystyle\lim_{x \to +\infty} F(x)$ et en déduire la nature de la branche infinie au voisinage de $+\infty$. (1pt)
-
- Montrer que : $(1pt)$ \[\left( {\forall x \in \left] {0,1} \right[} \right)\,\,:\,\,\,\,\,\,\,\frac{{x\left( {x – 1} \right)}}{{2\ln x}} \le F(x) \le \frac{{x\left( {x – 1} \right)}}{{\ln x}}\]
- Montrer que la fonction $F$ est continue à droite en $0$. (0.5pt)
- Montrez que la fonction $F$ est dérivable à droite en $0$ et interpréter le résultat obtenu. (0.75pt)
-
- Montrer que : (0.75pt) $$ \left(\forall x \in \left]0,1\right[ \cup \left]1,+\infty\right[\right) \,:\,\,\, \int_x^{x^2} \dfrac{dt}{t\ln t} = \ln 2$$
- Montrer que : $(1pt)$ $$ (\forall x > 1) \,:\,\, x \ln 2 \leq F(x) \leq x^2 \ln 2 $$
- Trouver un encadrement similaire sur l’intervalle $]0,1[$. (0.5pt)
- En déduire que la fonction $F$ est continue en $1$. (0.75pt)
-
- Montrer que : (0.75pt)\[\left( {\forall x > 1} \right)\left( {\exists {c_x} \in \left] {1,x} \right[} \right):\,\,\,\,\,\,F’\left( x \right) = \frac{{F\left( x \right) – F\left( 1 \right)}}{{x – 1}} = F’\left( {{c_x}} \right)\]
- Montrer que $F$ est dérivable en $1$ et que $F'(1) = 1$. (0.75pt)
-
- Dressez le tableau de variations de la fonction $F$. (0.5pt)
- Tracer $(C_F)$ la courbe représentative de $F.$ (0.5pt)
Partie III:
On considère la suite $(v_n)_{n \in \mathbb{N^*}}$ définie par : $$ v_n = \int_{e^n}^{e^{n+1}} \frac{dt}{\ln t} $$
- Montrer en utilisant un changement de variable que : (0.75pt) \[\left( {\forall n \in \mathbb{N}^*} \right),\quad {v_n} = \int_n^{n + 1} {\frac{{{e^t}}}{t}} dt\]
- On considère la fonction $f$ définie sur $]1, +\infty[$ par : $f(x) = \dfrac{e^x}{x}$.
- Montrer que $f$ est strictement croissante sur $]1, +\infty[$. (0.5pt)
- Montrer que : (0.75pt) \[\left( {\forall n \in\mathbb{N}^*} \right),\quad \frac{{{e^n}}}{n} \le \int_n^{n + 1} f (t)dt \le \frac{{{e^{n + 1}}}}{{n + 1}}\]
- Montrer que l’équation $\dfrac{e^x}{x}=\displaystyle\int_n^{n+1}f(t)dt$ admet une solution unique dans l’intervalle $[n,n+1]$. (0.75pt)
- Montrer que $\displaystyle\lim_{n \to +\infty} \frac{u_n}{n} = 1.$ (0.5pt)
-
- Montrer que $(\forall n\in\mathbb{N}^*)$: (0.75pt) $$ 0 \leq \int_n^{n+1} \frac{e^t}{t^2} dt \leq \frac{1}{n} \int_n^{n+1} \frac{e^t}{t} dt $$
- En déduire que : (0.5pt)\[\displaystyle\mathop {\lim }\limits_{n \to + \infty } \frac{{\displaystyle\int_n^{n + 1} {\frac{{{e^t}}}{{{t^2}}}dt} }}{{\displaystyle\int_n^{n + 1} {\frac{{{e^t}}}{t}dt} }} = 0\]
- Montrer en utilisant une intégration par parties que : (0.75pt) \[\left( {\forall n \in {\mathbb{N}^*}} \right),\quad \int_n^{n + 1} {\frac{{{e^t}}}{t}} dt = \frac{{{e^n}}}{n}\left( {\frac{{ne}}{{n + 1}} – 1} \right) + \int_n^{n + 1} {\frac{{{e^t}}}{{{t^2}}}} dt\]
- En déduire que : (0.75pt) $$ \lim (u_n-n) = \ln(e-1)$$
Durée : 2 heures

On considère la fonction $f$ définie par :
{f\left( x \right) = {x^2}\arctan \left( {\dfrac{1}{{x + 1}}} \right)}&;&{x \ge 0}\\
{}&{}&{}\\
{f\left( x \right) = \arctan \left( {\sqrt[3]{{\arctan x – x}}} \right)}&;&{x < 0}
\end{array}} \right.$
Soit $(C_f)$ sa courbe représentative dans un repère orthonormé $\left( {O,\overrightarrow i ,\overrightarrow j } \right)$
-
- Montrer que : $\left( {\forall x < 0} \right)\,\,;\,\,\,\arctan \left( x \right) – x > 0$. (0.75)
(0,75) - En déduire que la fonction $f$ est définie sur $\mathbb{R}$. (0.5pt)
(0,5)
- Montrer que : $\left( {\forall x < 0} \right)\,\,;\,\,\,\dfrac{{{x^5}}}{5} < \arctan \left( x \right) – x + \dfrac{{{x^3}}}{3} < 0$
(1,5) - Calculer : $\mathop {\lim }\limits_{x \to {0^ – }} \dfrac{{\arctan \left( x \right) – x}}{{{x^3}}}$
(0,75) - Étudier la dérivabilité de $f$ à gauche en $0$, puis interpréter graphiquement le résultat obtenu.(1)
- Étudier la dérivabilité de $f$ à droite en $0$, puis interpréter graphiquement le résultat obtenu.(1,5)
- Montrer que : $\left( {\forall x < 0} \right)\,\,;\,\,\,\arctan \left( x \right) – x > 0$. (0.75)
- Calculer $\mathop {\lim }\limits_{x \to – \infty } f\left( x \right)$, puis interpréter graphiquement le résultat obtenu.(0,75)
- Calculer $\mathop {\lim }\limits_{x \to +\infty } f\left( x \right)$
(1) - Montrer que : $\mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{\arctan \left( x \right) – x}}{{{x^2}}} = 0$
(Utiliser la question 2a)
(1) - Montrer que : $$\left( {\forall x > 0} \right)\,\,;\,\,\,\,\,f\left( x \right) – x = \dfrac{{{x^2}}}{{{{\left( {x + 1} \right)}^2}}}\left( {\dfrac{{\arctan \left( {\dfrac{1}{{x + 1}}} \right) – \dfrac{1}{{x + 1}}}}{{{{\left( {\dfrac{1}{{x + 1}}} \right)}^2}}}} \right) – \dfrac{x}{{x + 1}}$$
En déduire la nature de la branche infinie au voisinage de $+\infty$.
(0,75)
- Calculer $\mathop {\lim }\limits_{x \to +\infty } f\left( x \right)$
- On considère la fonction $g$ définie sur $]0,+\infty[$ par :
$$g\left( x \right) = 2\arctan \left( {\dfrac{1}{{x + 1}}} \right) – \dfrac{x}{{{x^2} + 2x + 2}}$$- Étudier les variations de la fonction $g$, puis en déduire que $g\left( x \right) > 0$
(1,5) - Étudier les variations de la fonction $f$, puis dresser le tableau de variations de $f$.
(1,5)
- Étudier les variations de la fonction $g$, puis en déduire que $g\left( x \right) > 0$
- Construire la courbe $(C_f)$.
(1)

On considère la fonction $f$ définie sur $\left]0,\dfrac{\pi}{3}\right]$ par :
$f(x)=\dfrac{\sin x}{x}$.
-
- Montrer que : $\left( {\forall x \in \left] {0,\dfrac{\pi }{3}} \right]} \right)\,\,;\,\,\,\,\,x\cos x – \sin x < 0$ (0,75)
- En déduire le sens de variation de $f$. (0,75)
- On considère la fonction $\varphi$ définie sur $\mathbb{R}$ par : $\varphi \left( x \right) = x\cos x – \sin x + c{x^2}$ où $c=\dfrac{\sqrt{3}}{4}$.
- Calculer $\varphi'(x)$, puis en déduire que : $\left( {\forall x \in \left] {0,\dfrac{\pi }{3}} \right]} \right)\,\,;\,\,\,\,\,\varphi \left( x \right) > 0$. (0,75)
- En déduire que : $\left( {\forall x \in \left] {0,\dfrac{\pi }{3}} \right]} \right)\,\,\,;\,\,\,\left| {f’\left( x \right)} \right| \le c$. (0,75)
- On considère la suite $(u_n)_{n\in \mathbb{N}}$ définie par : $\left\{ {\begin{array}{*{20}{l}} {{u_0} \in \left] {0,\dfrac{\pi }{3}} \right]} \\ {} \\ {{u_{n + 1}} = f\left( {{u_n}} \right)} \end{array}} \right.$
- Montrer que l’équation $\sin x=x^2$ admet une unique solution $\alpha$ dans $\left] {0,\dfrac{\pi }{3}} \right]$. (0,75)
- Montrer que : $\left( {\forall n \in \mathbb{N}} \right)\,\,;\,\,\,\,\,0 < {u_n} \le \dfrac{\pi }{3}$. (0,75)
- En utilisant le théorème des accroissements finis, montrer que :$\left( {\forall n \in \mathbb{N}} \right)\,\,;\,\,\,\,\,\left| {{u_{n + 1}} – \alpha } \right| \le c\left| {{u_n} – \alpha } \right|$. (1)
- En déduire que $(u_n)$ est convergente et calculer $\mathop {\lim }\limits_{n \to + \infty } {u_n}$. (1)

On considère la fonction $f$ définie sur $\left]0,\dfrac{\pi}{3}\right]$ par :
$f(x)=\dfrac{\sin x}{x}$.
-
- Montrer que : $\left( {\forall x \in \left] {0,\dfrac{\pi }{3}} \right]} \right)\,\,;\,\,\,\,\,x\cos x – \sin x < 0$ (0,75)
- En déduire le sens de variation de $f$. (0,75)
- On considère la fonction $\varphi$ définie sur $\mathbb{R}$ par : $\varphi \left( x \right) = x\cos x – \sin x + c{x^2}$ où $c=\dfrac{\sqrt{3}}{4}$.
- Calculer $\varphi'(x)$, puis en déduire que : $\left( {\forall x \in \left] {0,\dfrac{\pi }{3}} \right]} \right)\,\,;\,\,\,\,\,\varphi \left( x \right) > 0$. (0,75)
- En déduire que : $\left( {\forall x \in \left] {0,\dfrac{\pi }{3}} \right]} \right)\,\,\,;\,\,\,\left| {f’\left( x \right)} \right| \le c$. (0,75)
- On considère la suite $(u_n)_{n\in \mathbb{N}}$ définie par : $\left\{ {\begin{array}{*{20}{l}} {{u_0} \in \left] {0,\dfrac{\pi }{3}} \right]} \\ {} \\ {{u_{n + 1}} = f\left( {{u_n}} \right)} \end{array}} \right.$
- Montrer que l’équation $\sin x=x^2$ admet une unique solution $\alpha$ dans $\left] {0,\dfrac{\pi }{3}} \right]$. (0,75)
- Montrer que : $\left( {\forall n \in \mathbb{N}} \right)\,\,;\,\,\,\,\,0 < {u_n} \le \dfrac{\pi }{3}$. (0,75)
- En utilisant le théorème des accroissements finis, montrer que :
$\left( {\forall n \in \mathbb{N}} \right)\,\,;\,\,\,\,\,\left| {{u_{n + 1}} – \alpha } \right| \le c\left| {{u_n} – \alpha } \right|$. (1)
- En déduire que $(u_n)$ est convergente et calculer $\mathop {\lim }\limits_{n \to + \infty } {u_n}$. (1)
Durée : 2 heures

- Montrer que : $2 \arctan \left( \dfrac{1}{3} \right) + \arctan \left( \dfrac{1}{7} \right) = \dfrac{\pi}{4}$
- Calculer : $\displaystyle\lim_{x \to -\infty} \dfrac{\sqrt[3]{-x}+x}{\sqrt{-x}+x}$
- Calculer : $\displaystyle\lim_{x \to 1^{-}} \dfrac{\sqrt[3]{1-x}+x^2-1}{x-1}$
- Calculer : $\displaystyle\lim_{x \to 1^{+}} \dfrac{\arctan\left( \sqrt[3]{1-x}\right)}{x-1}$
- Montrer que : $(\forall x<0)\,;\,\,\, \arctan x+\arctan\dfrac{1}{x}=-\dfrac{\pi}{2}$
- En déduire : $\displaystyle\lim_{x \to +\infty} \left(2x\arctan\left(1-\sqrt[3]{x} \right)+\pi x\right)$

- Montrer que $(\forall p\in \mathbb{N})$ : \[\arctan \left( p+1 \right) + \arctan \left( p \right) = \arctan \left( \dfrac{1}{p^2+p+1} \right)\]
- On considère la suite $(S_n)_{n\in\mathbb{N}}$ définie par : $$S_n=\sum_{k=0}^{n}\arctan\left(\dfrac{1}{k^2+k+1}\right)$$
Calculer $S_n$ en fonction de $n$ puis calculer $\displaystyle\lim_{n \to \infty} S_n$.

Pour tout entier $n\ge 3$, on considère la fonction $f_n$ définie par $f_n(x) =x^n-2-n(x-1)$.
- Montrer que l’équation $f_n(x)=0$ admet une unique solution $x_n$ dans $[0,1]$.
- Étudier la monotonie de la suite $(x_n)$ et déduire que $(x_n)$ est convergente.
- Montrer que $(\forall n\ge 3)\,:\,\, x_n=\dfrac{n+x_n^n-2}{n}$.
- En déduire un encadrement de $(x_n)$, puis calculer $\lim x_n.$

Soient $f$ et $g$ deux fonctions continues de $[0,1]$ dans $[0,1]$ telles que $f \circ g = g \circ f$.
Le but de l’exercice est de démontrer qu’il existe $c \in [0,1]$ tel que $f(c) = g(c)$.
- Montrer qu’il existe $s \in [0,1]$ tel que $f(s) = s$.
- Montrer que pour tout $n \ge 0$, $g^n(s) = f(g^n(s))$. (On pourra utiliser un raisonnement par récurrence)
(Où $g^n = \underbrace{g \circ g \circ g \circ \dots \circ g}_{n\,fois}$ pour $n \ge 1$ et $g^0 = Id\, :\, x \to x$)
- On considère la suite $\left( u_n \right)_{n \in \mathbb{N}}$ définie par : $u_n = g^n(s)$ pour tout $n \in \mathbb{N}$.
- Vérifier que $f(u_n) = u_n$ et que $u_{n+1} = g(u_n)$.
- Montrer que pour tout $n \in \mathbb{N}$, $0 \le u_n \le 1$.
- On suppose que la suite $(u_n)$ est monotone. Montrer que la suite $(u_n)$ est convergente et que sa limite $\ell$ vérifie $f(\ell) = g(\ell)$.
- On suppose que la suite $(u_n)$ n’est pas monotone. Montrer qu’il existe $(u,v) \in [0,1]^2$ tels que $\left( f(u) – g(u) \right)\left( f(v) – g(v) \right) \le 0$.
- Conclure.

On considère la fonction $g$ définie sur $[0,\pi[$ par : $g(x) = \arctan \left( \sqrt{\dfrac{1-a}{1+a}} \tan \left( \dfrac{x}{2} \right) \right)$.
Soit $f$ une fonction continue sur $[0,\pi]$ telle que : $(\forall x\in [0,\pi[),\,\, f(x)=\pi-2g(x)$
- Calculer $f(\pi)$.
- Montrer que pour tout $x \in ]0,\pi[$ : \[0 < f(x) < \pi\]
- Montrer que pour tout $x \in ]0,\pi[$ : \[\tan \left( \dfrac{f(x)}{2} \right) \tan \left( \dfrac{x}{2} \right) = \sqrt{\dfrac{1+a}{1-a}}\]
- En déduire que pour tout $x\in [0,\pi],\,\,\,f(f(x)) = x$.
- En déduire que la fonction $f$ est une bijection de $[0,\pi]$ vers $[0,\pi]$ et en déduire la bijection réciproque $f^{-1}$.

On considère la fonction $ f(x)=\dfrac{x^{2}+4 x+1}{x^{2}+1} $.
- Montrer que $3$ est le maximum absolu de $f$ atteint en $x=1$.
- Montrer que $-1$ est le minimum absolu de $f$.

On considère la fonction $ f(x)=\dfrac{4 x-3}{x^{2}+1} $.
- Montrer pour tout $ x $ et $ y $ de $\mathbb{R}$ tel que $ x \neq y $, on a : $$ \dfrac{f(x)-f(y)}{x-y}=\dfrac{(2 x+1)(2-y)+(2 y+1)(2-x)}{\left(x^{2}+1\right)\left(y^{2}+1\right)}.$$
- En déduire les variations de $ f $ sur $ [2,+\infty[ $, $ \left[-\dfrac{1}{2}, 2\right] $, et $ \left]-\infty,-\dfrac{1}{2}\right] $.
- Déterminer le maximum et le minimum absolus de $ f $.
- Montrer que $ f\left(\left[2,+\infty\right[\right)=\left] 0,1\right]$.
- On considère la fonction $g(x)=\dfrac{4x-3x^2}{1+x^2}.$
- Montrer que $(\forall x\neq 0)\,:\,\,\, g(x)=f\left(\dfrac{1}{x}\right).$
- En déduire les variations de la fonction $g$ sur chacun des intervalles : \[\left[ {2, + \infty } \right[\,\,,\,\,\left[ {\frac{1}{2},2} \right]\,\,,\,\,\left] {0,\frac{1}{2}} \right]\,\,,\,\,\left[ { – \frac{1}{2},0} \right[\,\,,\,\,\left[ { – 2, – \frac{1}{2}} \right]\,\,,\,\,\left] { – \infty , – 2} \right]\]

On considère les deux fonctions : $f(x)=\sqrt{x+1}$ et $g(x)=-x^3$.
- Construire dans un même repère les courbes $ C_f $ et $ C_g $.
- En déduire que l’équation $ x^{3}+\sqrt{1+x}=0 $ admet une solution unique $ \alpha $ telle que $ -\dfrac{7}{8}<\alpha<-\dfrac{3}{4}.$
- Résoudre dans $ \left[-1,+\infty\right[ $ l’inéquation $ x^{3}+\sqrt{1+x}<0.$
- Déterminer graphiquement $ f\left(\left[-1,2\right]\right) $ et $ f\left(\left[3,+\infty\right[\right).$

On considère les fonctions $ f(x)=\sqrt{x+1} $ et $ g(x)=\dfrac{x+1}{x-2}.$
Déterminer le domaine de définition de $ h=g \circ f $ puis étudier ses variations.

On considère les fonctions $ f(x)=x^{2}-2x $ et $ g(x)=x^{2}-4x+5.$
Étudier les variations de la fonction $ h=g \circ f.$

On considère la fonction $ f(x)=\dfrac{8 x+4}{x^{2}+2 x+1}.$
- Déterminer $ D_f.$
- Montrer que $f$ admet un maximum absolu.
- On considère la fonction $ g(x)=4-x^{2} $.
- Déterminer une fonction $ h $ telle que $ \left(\forall x \in D_f\right)\,: \,\,\,f(x)=g \circ h(x)$.
- En déduire les variations de $f$.

On considère la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=x^{3}+x^{2}+x $.
-
- Montrer que $ \left(\forall (x, y) \in \mathbb{R}^2\right)\,:\,\,\, x^{2}+x(1+y)+y^{2}+y+1 > 0.$
- En déduire que $f $ est croissante sur $ \mathbb{R} $.
- On considère la fonction $g$ définie sur $\mathbb{R}_+^*$ par : $ g(x)=\dfrac{1+x+\sqrt{x}}{x\sqrt{x}} $.
- Montrer que $ \left(\forall x \in \mathbb{R}_+^*\right)\,:\,\,\, g(x)=f\left(\dfrac{1}{\sqrt{x}}\right).$
- En déduire les variations de $g$ sur $ \mathbb{R}_+^*.$

On considère la fonction $f$ définie sur $\mathbb{R}$ par : $f(x)=\sqrt{x+\sqrt{x^{2}+1}}$.
- Déterminer $D_f$.
- Monsrer que $\left(\forall x \in D_f\right)\,:\,\,\, f(-x)=\dfrac{1}{f(x)}$.
- Étudier les variations de $f$ sur $\mathbb{R}^{+}$ puis sur $\mathbb{R}^{-}$.
- Soit $g$ la restriction de $f$ sur $\mathbb{R}^{+}$.
Montrer que $g$ est une bijection de $\mathbb{R}^{+}$ sur $[1,+\infty[$ puis déterminer sa bijection réciproque.

On considère la fonction $f(x)=\dfrac{1}{x+1}\sqrt{x^{2}-1}$.
- Déterminer $D_f$.
- On considère la fonction $g$ définie par : $g(x)=(f(x))^{2}$.Donner le tableau de variation de $g$ puis celui de $f$.

On considère la fonction $f$ définie par : $ f(x)=\dfrac{\sqrt{1+x^{2}}-1}{x} $ pour $ x \neq 0 $ et $ f(0)=0 $.
- Montrer que $ \left(\forall x \in \mathbb{R}\right)\,:\,\, -1 < f(x) <1$.
- Monsrer que $1$ et $-1$ ne sont pas des extremums de la fonction $f$.

On considère la fonction $f$ définie sur $]0,1[$ par : $ f(x)=\left(1+\dfrac{1}{x}\right)\left(1+\dfrac{1}{1-x}\right).$
- Montrer que $ \left(\forall x \in ]0,1[\right)\,:\,\, f(x)=1-\dfrac{2}{x^{2}-x}.$
- Étudier les variations de la fonction $f$ sur chacun des intervalles $\left]0, \dfrac{1}{2}\right[$ et $\left]\dfrac{1}{2},1\right[$.
- Quelle est la valeur maximale que prend le nombre $ A=\left(1+\dfrac{1}{a}\right)\left(1+\dfrac{1}{b}\right)$ lorsque $a$ et $b$ sont des réels strictement positifs vérifiant $a+b=1$?

On considère la fonction définie sur $[1,+\infty[$ par $f(x)=x-1-2 \sqrt{x-1}.$
- Déterminer $A=f^{-1}\left(\left\{-\dfrac{1}{2}\right\}\right)$ et en déduire que $f$ n’est pas injective.
- On considère les deux fonctions $u(x)=x^{2}-2 x$ et $v(x)=\sqrt{x-1}.$
- Montrer que pour tout $x \in[1,+\infty[$, on a : $f(x)=(u \circ v)(x).$
- Étudier les variation de $f$.
- En déduire que $f$ n’est pas surjective de $[1,+\infty[$ vers $\mathbb{R}$.
- Déterminer le maximum absolu de la fonction $g(x)=\dfrac{1}{x}\left(1-2 \sqrt{x-x^{2}}\right)-1$ sur l’intervalle $\left[\dfrac{2}{5}, \dfrac{1}{2}\right]$

On considère la fonction $f(x)=\dfrac{\sqrt{|x|}-2}{\sqrt{|x|}+2}.$
- Déterminer le domaine de définition de $f$ et étudier sa parité.
- Étudier les variations de $f$.
- Montrer que pour tout $x \in \mathbb{R}$, on a : $-1 \leq f(x) < 1.$
- Montrer que $-1$ est le minimum absolu de $f$, et que $f$ n’admet pas de maximum absolu.
- Montrer que $f$ est une bijection de $\mathbb{R}^{+}$ vers $[-1,1[$, puis déterminer sa bijection réciproque.

On considère la fonction $f$ définie sur $\mathbb{R}^{+}$par $f(x)=\dfrac{1+\sqrt{x}}{\sqrt{1+x}}+\sqrt{1+x}.$
- Montrer que $-1$ est le minimum absolu de $f$.
- Montrer que la fonction $f$ n’est pas majorée.

On considère les deux fonctions définies par : $f(x)=x^{2}-2 x+2$ et $g(x)=\sqrt{x-1}+1.$
- Étudier les variations des deux fonctions $f$ et $g$.
- Soit $h$ la restriction de $f$ à l’intervalle $[1,+\infty[$.
- Montrer que $f \circ h$ et $h\circ f$ sont définies sur $[1,+\infty[$.
- Montrer que $f \circ h=h \circ f=Id$.
- En déduire que $f$ et $h$ sont des bijections de $[1,+\infty[$ vers $[1,+\infty[$ et déterminer leur bijection réciproque.

On considère la fonction $f$ définie sur $[0,12]$ par : $f(x)=\sqrt{x}+\sqrt{12-x}.$
-
- Montrer que $(\forall x \in[0,12])\,:\,\,\, 12-x \in[0,12]$ et $f(12-x)=f(x)$.
- Montrer que pour tout $(x, y) \in\mathbb{R}^{2}$ les points $M(x, y)$ et $M(12-x, y)$ son symétriques par rapport à la droite $(D)\,:\,\,\, x=6$.
- En déduire que la droite $(D)\,:\,\,\, x =6$ est un axe de symétrie de la courbe $\left(C_{f}\right)$.
- Étudier les variation de la fonction $f$ sur $[0,6]$ puis sur $[6,12]$.
- En déduire la comparaison des nombres $\sqrt{2}+\sqrt{10}$, $\sqrt{3}+3$ et $\sqrt{5}+\sqrt{7}.$

On considère la fonction $f$ définie sur $\mathbb{R}^{+}$ par : $f(x)=E\left(x^{2}\right)-2 E(x).$
-
- Montrer que $\left(\forall x \in\mathbb{R}^{+}\right)\,:\,\,\,(E(x))^{2} \leq E\left(x^{2}\right)$.
- En déduire que $-1$ et le maximum absolu de $f$.
- On pose $x=n+\dfrac{1}{2}$ avec $x \in\mathbb{N}$.
- Calculer $f(x)$ en fonction de $n$.
- En déduire que $f$ n’est pas majorée.