
On considère la fonction affine $g$ définie par : $g(x)=-2x+1$.
- Calculer : $g(-5)$, $g\left(\dfrac{3}{2}\right)$, et $g\left(f(2)\right)$
- Calculer l’image de $-3$ par $g$.
- Quelle est l’image de $4$ par $g$.
- Déterminer le nombre dont l’image est $13$.
- Calculer l’antécédent de $-7$ par $g$.
- Tracer dans un repère la courbe de $g$.
- Par lecture graphique déterminer :
- L’image de $-2$ par $g$.
- L’antécédent de $4$ par $g$.

Soit $f$ une fonction affine telle que : $f(-1)=-7$ et $f(3)=5$.
- Déterminer le coefficient de $f$.
- Déterminer l’expression de $f$.
- Sans calcul déterminer la valeur de : $\dfrac{f(2026)-f(1989)}{2026-1989}$

Soient $f$ une fonction affine et $(\Delta)$ sa représentation graphique. $M(-2;3)$ et $N(5;-4)$ deux points de la droite $(\Delta)$.
- Déterminer le coefficient de $f$.
- Déterminer l’expression de $f$.
- Le point $P(9;6)$ appartient-il à $(\Delta)$?

On considère $(D)$ la représentation graphique de la fonction $h$.
- Déterminer la nature de la fonction $h$.
- Déterminer graphiquement :
- L’image de $1$ par $h$.
- L’antécédent de $-1$ par $h$.
- Le nombre dont l’image est $4$ par $h$.
- Le nombre dont l’antécédent est $2$ par $h$.
- Montrer que l’expression de $h$ est : $h(x)=2x+1$.
- Résoudre l’équation : $h(x)=0$.

On considère la fonction linéaire $f$ définie par : $f(x)=-4x$.
- Calculer : $f(-2)$, $f(\sqrt{3})$ et $f(f(5))$
- Calculer l’image de $1,5$ par $f$.
- Quelle est l’image de $8$ par $f$.
- Déterminer le nombre dont l’image est $10$.
- Calculer l’antécédent de $20$ par $f$.
- Tracer dans un repère la courbe de $f$.
- Déterminer graphiquement :
- L’image de $-1$ par $f$.
- L’antécédent de $1$ par $f$.

Soit $f$ une fonction linéaire telle que : $f(-3)=7$.
- Déterminer le coefficient de $f$.
- Déterminer l’expression de $f$.

Soient $f$ une fonction linéaire et $(\Delta)$ sa représentation graphique, soit $M(-2;3)$ un point de $(\Delta)$.
- Déterminer le coefficient de $f$, puis donner l’expression de $f$.
- Sans calcul déterminer la valeur de : $\dfrac{f(2026)}{2026}$.

On considère $(D)$ la représentation graphique de la fonction $f$.
- Déterminer la nature de la fonction $f$.
- Déterminer graphiquement :
- L’image de $1,5$ par $f$.
- L’antécédent de $-1$ par $f$.
- Le nombre dont l’image est $4$ par $f$.
- Le nombre dont l’antécédent est $1$ par $f$.
- Déterminer l’expression de $f$.

On considère le système suivant :$$\left\{ \begin{aligned}
& 2x+3y = 16\\
& 5x-2y = 21
\end{aligned} \right.$$
- Le couple $(2;4)$ est-il solution de ce système ?
- Le couple $(5;2)$ est-il solution de ce système ?

Résoudre par la méthode de substitution les systèmes suivants :
\begin{array}{lcl}
\displaystyle \mathbf 1.\ \left\{ \begin{aligned}
& 3x + y = – 3\\
& 2x – 4y = – 16
\end{aligned} \right. &&\displaystyle \mathbf 2.\ \left\{ \begin{aligned}
& 4x -5y = 0\\
& 5x – 4y = 9
\end{aligned} \right.\\
\displaystyle \mathbf 3.\ \left\{ \begin{aligned}
&\dfrac{x}{3}=\dfrac{y}{4}\\
&x-y=-\dfrac{2}{3}\end{aligned} \right. &&
\displaystyle \mathbf 4.\ \left\{ \begin{aligned}
& x+\sqrt{2} y = 3\\
&-\sqrt{2}x+y= -\sqrt{2}
\end{aligned} \right.
\end{array}

Résoudre par la méthode de combinaison linéaire les systèmes suivants :
\begin{array}{lcl}
\displaystyle \mathbf 1.\ \left\{ \begin{aligned}
& 4x -5y = – 6\\
& 3x +2y = 7
\end{aligned} \right. &&\displaystyle \mathbf 2.\ \left\{ \begin{aligned}
& 3x +y = 2\\
& 3x +2y = 5
\end{aligned} \right.\\
\displaystyle \mathbf 3.\ \left\{ \begin{aligned}
& 3x-2y = 4\\
& x+2y=0
\end{aligned} \right. &&\displaystyle \mathbf 4.\ \left\{ \begin{aligned}
& -5x-7y = -4\\
& 5x+3y= 10
\end{aligned} \right.\end{array}

Résoudre graphiquement les systèmes suivants :
\begin{array}{lcl}
\displaystyle \mathbf 1.\ \left\{ \begin{aligned}
& -7x + y = 4\\
& 6x – 3y = 3
\end{aligned} \right. &&\displaystyle \mathbf 2.\ \left\{ \begin{aligned}
& x -2y = -8\\
& 3x +2y = 0
\end{aligned} \right.\\
\displaystyle \mathbf 3.\ \left\{ \begin{aligned}
& 4x-2y = 3\\
& 2x-y=1
\end{aligned} \right. &&\displaystyle \mathbf 4.\ \left\{ \begin{aligned}
& 2x+y-5= 0\\
& 8x+4y+4=12
\end{aligned} \right.
\end{array}

Trouver deux nombres réels sachant que leur somme est $297$ et leur différence est $49$.

Dans une entreprise de $250$ employé, il y a quatre fois plus d’hommes que de femmes.
Calculer le nombre d’hommes et le nombre de femmes dans cette entreprise.

Dans un repère orthonormé $(O;I;J)$ on considère la droite $(D):\,\, y=3x-1$
- Donner le coefficient directeur et l’ordonnée à l’origine de la droite $(D)$.
- Le point $A(0;2)$ est-il un point de la droite $(D)$? Justifier.
- Le point $B(-1;-4)$ est-il un point de la droite $(D)$? Justifier.
- Déterminer $a$ tel que $M(a;3)$ soit un point de la droite $(D)$.
- Tracer la droite $(D)$.

Dans un repère orthonormé $(O;I;J)$, tracer les droites $(\Delta):\,\, y=\dfrac{1}{2}x-5$ et $(L):\,\, y=4x-3.$

Dans un repère orthonormé $(O;I;J)$, on donne les points : $$A(1;-1)\,\,\,;\,\,\,B(3;5)\,\,\,;\,\,\,C(2;7)\,\,\,;\,\,\,D(-1;-2)\,\,\,;\,\,\,E(2;-1)\,\,\,;\,\,\,F(-1;5).$$
- Donner les équations des droites $(AB)$; $(CD)$ et $(EF)$
- Comment sont les droites $(AB)$ et $(CD)$ ? Justifier.
- Montrer que $(AB)$ et $(EF)$ sont sécantes.

Dans un repère orthonormé $(O;I;J)$, on donne : $$(L):\,\, y= -\dfrac{1}{2}x+\dfrac{5}{2}\,\,\,;\,\,\,A(3;-1)\,\,\,;\,\,\,B(2;-5).$$
- Donner l’équation de la droite $(D)$ la parallèle à $(L)$ passant par $A$.
- Donner l’équation de la droite $(\Delta)$ le perpendiculaire à $(L)$ passant par $B$.

Dans un repère orthonormé $(O;I;J)$, on donne les points: $$A(7;-1)\,\,\,;\,\,\,B(3;-5)\,\,\,;\,\,\,M(5;-3).$$
- Vérifier que $M$ est le milieu de $[AB]$.
- Donner le coefficient directeur de la droite $(AB)$.
- Donner l’équation de la droite $(\Delta)$ la médiatrice de $[AB]$.

Soit $(O;I;J)$ un repère orthonormé.
- Construire les points : $A\left(-\dfrac{3}{2};4\right)$ ; $B(0;-2)$ ; $C(3;0)$
- Soient $M$ un point de l’axe des abscisses, et $N$ un point de l’axe des ordonnées.
Déterminer l’ordonnée de $M$ et l’abscisse de $N$.

Soit $(O;I;J)$ un repère orthonormé. On considère les points : $$A(3;1)\,\,;\,\,B(-5;2)\,\,;\,\,C(0;4)\,\,;\,\, D(-1;-2)$$Déterminer les coordonnées des vecteurs : $\overrightarrow{AB}$; $\overrightarrow{AC}$; $\overrightarrow{BC}$; $\overrightarrow{CD}$

Soit $(O;I;J)$ un repère orthonormé. On considère les points :
$$A(-1;-1)\,\,;\,\,B(4;4)\,\,;\,\,C(5;1)\,\,;\,\,D(x;y)$$
- Déterminer $x$ et $y$ pour que le quadrilatère $ABCD$ soit un parallélogramme.
- Déterminer Les coordonnées du point $M$ le milieu du segment $[AC]$.
- Déterminer Les coordonnées de $N$ le sachant que $A$ est le milieu d segment $[BN]$.
- Calculer la distance $AB$.

Soit $(O;I;J)$ un repère orthonormé. On considère les points :
$$A(-2;-2)\,\,;\,\,B(3;0)\,\,;\,\,C(-1;2)$$Déterminer Les coordonnées des vecteurs :
$$\overrightarrow{AB}+\overrightarrow{AC}\,\,;\,\,-5\overrightarrow{AB}\,\,;\,\,2\overrightarrow{AB}-\dfrac{3}{2}\overrightarrow{BC}$$

Soit $(O;I;J)$ un repère orthonormé. On considère les points :
$$A(-1;1)\,\,;\,\,B(3;3)\,\,;\,\,C(5;-1)$$
- Construire Les points $A$, $B$ et $C$
- Calculer les distances $AB$, $BC$ et $AC$.
- Montrer que le triangle $ABC$ est rectangle et isocèle.

Soit $ABC$ un triangle.
- Construire le point $M$ tel que : $\overrightarrow {AM}= \overrightarrow {BC} $.
- Construire le point $N$ tel que : $\overrightarrow {AN}= \overrightarrow {CB} $.
- Montrer que $A$ est le milieu du segment du segment $[MN]$.

Soit $ABCD$ un parallélogramme de centre $O$.
- Construire le point $N$ tel que : $\overrightarrow {AO}= \overrightarrow {BN} $.
- Montrer que $ONCD$ est un parallélogramme.

Soient $ABCD$ un parallélogramme, et $I$ le milieu du segment $[BC]$.
- Construire $E$ le symétrique de $A$ par rapport à $I$.
- Construire $J$ le le milieu de $[BE]$.
- Construire $F$ le symétrique de $A$ par rapport à $J$.
- Montrer que : $\overrightarrow {DC}=\overrightarrow {CE}=\overrightarrow {EF}$.

Soit $ABCD$ un parallélogramme.
- Construire les points $M$ et $N$ tels que :
$\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {AC} ~~~~\text{et}~~~~ \overrightarrow {AN} = \overrightarrow {AC} + \overrightarrow {AD}$ - Montrer que : $\overrightarrow {BD}=\overrightarrow {MN}$.

Soit $ABC$ un triangle, et $I$ le milieu du segment $[BC]$.
- Construire les points $D$ tel que :
$\overrightarrow {CD} = \overrightarrow {CA} + \overrightarrow {IB}$. - Montrer que : $\overrightarrow {DB}=\overrightarrow {AI}$.

Simplifier les vecteurs suivants :
- $\overrightarrow {EF} + \overrightarrow {GE} + \overrightarrow {FG}$
- $\overrightarrow {AB} – \overrightarrow {BD} + \overrightarrow {CA} – \overrightarrow {CB}$
- $\overrightarrow {FE} – \overrightarrow {GE} – \overrightarrow {GF} + \overrightarrow {GH} + \overrightarrow {GF}$
- $\overrightarrow {ED} + \overrightarrow {BA} + \overrightarrow {DC} – \overrightarrow {EA} – \overrightarrow {BC}$

Soit $ABC$ un triangle.
- Construire les points $E$ et $F$ tels que : $\overrightarrow {AE} = 2\overrightarrow {AB}$ et $\overrightarrow {AF} = 2\overrightarrow {AC}$.
- Montrer que : $\overrightarrow {BE}=\overrightarrow {AB}$.
- Montrer que : $\overrightarrow {EF}=2\overrightarrow {AB}$.

Soit $ABC$ un triangle.
- Construire les points $M$ et $N$ tels que :
$\overrightarrow {AM} = 3\overrightarrow {AB}$ et $\overrightarrow {CN} = -2\overrightarrow {CA}$. - Montrer que : $\overrightarrow {AN}=3\overrightarrow {AC}$.
- Montrer que : $\overrightarrow {MN}=3\overrightarrow {BC}$.
- En déduire que : $(MN)\parallel (BC)$.

Soit $ABCD$ un parallélogramme.
- Construire les points $E$ et $F$ tels que :
$\overrightarrow {AE} = -\dfrac{1}{2}\overrightarrow {AD}$ et $\overrightarrow {EF} = \dfrac{1}{2}\overrightarrow {BA}$. - Montrer que les points $A$, $C$ et $F$ sont alignés.

Soit $ABC$ un triangle, $I$, $J$ et $K$ trois points tels que :
$$\overrightarrow {BI} = \dfrac{3}{2}\overrightarrow {BC}
~~;~~
\overrightarrow {CJ} = \dfrac{1}{3}\overrightarrow {CA}
~~;~~
\overrightarrow {AK} = \dfrac{2}{5}\overrightarrow {AB} $$
- Construire les points $I$, $J$ et $K$.
- Montrer que : $\overrightarrow {IJ} = – \dfrac{1}{2}\overrightarrow {BC} – \dfrac{1}{3}\overrightarrow {AC} $
- Montrer que : $\overrightarrow {JK} = – \dfrac{2}{5}\overrightarrow {BC} – \dfrac{4}{{15}}\overrightarrow {AC}$
- En déduire que les points $I$, $J$ et $K$ sont alignés.

Soit $ABCD$ un parallélogramme.
- Construire $E$ l’image de $A$ par la translation qui transforme $B$ en $D$.
- Construire $F$ l’image de $B$ par la translation qui transforme $A$ en $C$.
- Montrer que $E$ est l’image de $D$ par la translation qui transforme $C$ en $D$.
- Montrer que $F$ est l’image de $C$ par la translation qui transforme $D$ en $C$.
- En déduire que : $\overrightarrow {ED} = \overrightarrow {DC} = \overrightarrow {CF} $ et $\overrightarrow {EF} \,\, = \,\,3\overrightarrow {AB} $

Soit $ABCD$ un parallélogramme de centre $O$.
- Construire $E$ l’image de $D$ par la translation du vecteur $\overrightarrow {AC}$.
- Construire $F$ le symétrique de $D$ par rapport à $A$.
- Montrer que $O$ est le milieu du segment $[EF]$.

Soit $EFGH$ un carré tel que $EF=3cm$.
- Construire $A$ l’image de $F$ par la translation du vecteur $\overrightarrow {EG}$.
- Construire $B$ l’image de $H$ par la translation du vecteur $\overrightarrow {EG}$.
- Déterminer la distance $AB$.

Soient $ABC$ un triangle et $[AH]$ sa hauteur.
- Construire $B’$ et $C’$ les images respectives de $B$ et $C$ par la translation du vecteur $\overrightarrow {AH}$.
- Déterminer l’image de la droite $(BC)$ par la translation du vecteur $\overrightarrow {AH}$.
- Montrer que $\left( {AH} \right) \bot \left( {B’C’} \right)$.

Soit $ABCD$ un parallélogramme de centre $O$.
- Construire $E$ l’image de $A$ par la translation du vecteur $\overrightarrow {OD}$.
- Construire $F$ l’image de $C$ par la translation du vecteur $\overrightarrow {OD}$.
- Montrer que les points $D$, $E$ et $F$ sont alignés.

Soient $ABC$ un triangle rectangle $A$, et $E$ un point du segment $[BC]$.
- Construire $B’$ et $C’$ les images respectives de $B$ et $C$ par la translation du vecteur $\overrightarrow {AE}$.
- Montrer que le triangle $EB’C’$ est rectangle.
- Montrer que $(BC)\parallel(B’C’)$.

Soient $O$ et $O’$ deux points du plan, soit le cercle $(\mathscr{C})$ de centre $O$ et de rayon $r=\dfrac{1}{4}OO’$.
- Construire $(\mathscr{C}’)$ l’image du cercle $(\mathscr{C})$ par la translation du vecteur $\overrightarrow {OO’}$.
- Soient $E$ un point de $(\mathscr{C})$ et $E’$ un point du plan tel que $OEE’O’$ est un parallélogramme. Montrer que le point $E’$ appartient au cercle $(\mathscr{C}’)$.

Résoudre les équations suivantes:
\begin{array}{lcl}
\displaystyle \mathbf 1.\ x+\sqrt{2}=3\sqrt{2} &&\displaystyle \mathbf 2.\ 4x-5=x+\dfrac{1}{2}\\[0.1cm]
\displaystyle \mathbf 3.\ 2x+1=\sqrt{3}x+4 &&\displaystyle \mathbf 4.\ 4x-4\sqrt{7}=x+2\sqrt{7}\\[0.1cm]
\displaystyle \mathbf 5.\ 2(x+3)-3x=-4(-x-5) &&\displaystyle \mathbf 6.\ \sqrt{3}(x+\sqrt{3})=2(x-\sqrt{3})\\[0.1cm]
\displaystyle \mathbf 7.\ \dfrac{x}{2}+\dfrac{3}{2}=\dfrac{2x}{3}-\dfrac{5}{2} &&\displaystyle \mathbf 8.\ \dfrac{x+1}{3}=\dfrac{2x-4}{5}\\[0.1cm]
\displaystyle \mathbf 9.\ \dfrac{4+x}{3}-\dfrac{2x-1}{8}=\dfrac{x+4}{4}&&\displaystyle \mathbf \
\end{array}

Résoudre les équations suivantes:
\begin{array}{lcl}
\displaystyle \mathbf 1.\ (3x-3)(x-4)=0 &&
\displaystyle \mathbf 2.\ (x+1)(2x-3)-(2x-3)(4x+2)=0 \\[0.1cm]
\displaystyle \mathbf 3.\ \sqrt{2}x^2=\sqrt{3}x &&
\displaystyle \mathbf 4.\ x^2-x=6x-6 \\[0.1cm]
\displaystyle \mathbf 5.\ (x-\sqrt{5})(x-1)=2x(x-\sqrt{5}) &&
\displaystyle \mathbf 6.\ x^2-3=0 \\[0.1cm]
\displaystyle \mathbf 7.\ (x-3)(2x+4)=4x^2-16 &&
\displaystyle \mathbf 8.\ 4(x+1)^2=(x-3)^2 \\[0.1cm]
\displaystyle \mathbf 9.\ (4x-1)^2-25=0 &&
\displaystyle \mathbf 10.\ 9x^2-6x=(5x+7)^2-1
\end{array}

Résoudre les inéquations suivantes:
\begin{array}{lcl}
\displaystyle \mathbf 1.\ x-4 \leq 0 &&
\displaystyle \mathbf 1.\ x+2 \geq 0 \\[0.1cm]
\displaystyle \mathbf 1.\ 3x > 9 &&
\displaystyle \mathbf 1.\ -2x \leq 4 \\[0.1cm]
\displaystyle \mathbf 1.\ 2x-3 > x+5 &&
\displaystyle \mathbf 1.\ 4x-1 \leq 2(x-1)+3 \\[0.1cm]
\displaystyle \mathbf 1.\ -5x+2 \geq 2x+9 &&
\displaystyle \mathbf 1.\ -3(x+2) < x+7 \\[0.1cm]
\displaystyle \mathbf 1.\ \dfrac{x+3}{3} < \dfrac{x+2}{2} &&
\displaystyle \mathbf 1.\ \dfrac{x-4}{2}-\dfrac{x-5}{4} \geq \dfrac{3x-1}{8}
\end{array}

Imad et Laila pèsent ensemble $135Kg$.
Sachant que Imad pèse $15Kg$ de plus que Laila, Trouver la masse de chacun d’eux.

Un club de football propose les tarifs suivants :
- Tarif 1 : 40 dirhams par billet.
- Tarif 2 : une carte d’abonnement pour la saison à 360 dirhams, permettant d’acheter chaque billet à 16 dirhams.
Question — À partir de combien de billets l’abonnement est-il avantageux ? Justifier.
Fonctions affines
La relation $f$ qui, à tout nombre réel $x$, associe le nombre $ax+b$, est appelée une fonction affine de coefficient $a$.
On la note :
$$f : x \mapsto ax+b$$
Le nombre $ax+b$ est l’image de $x$ par $f$, et on écrit : $f(x)=ax+b.$
Exemple : On considère la fonction définie par :
$$g(x)=-5x+3$$
- $g$ est une fonction affine de coefficient $-5$. $\,\,(a=-5 \text{ et } b=3)$.
- On a : $g(-2)=-5\times (-2)+3=10+3=13$. Donc, l’image de $-2$ par $g$ est $13.$
- On a : $g(7)=-5\times (7)+3=-35+3=-32$. Donc, l’antécédent de $-32$ par $g$ est $7.$
- Toute fonction linéaire est une fonction affine particulière de la forme :
$$f(x)=ax+0=f(x)=ax.$$ - Toute fonction constante est une fonction affine particulière de la forme :
$$f(x)=0\times x+b=f(x)=b.$$
Coefficient d’une fonction affines
Si $f$ est une fonction affine, alors $\dfrac{f(x_1)-f(x_2)}{x_1-x_1}$ est le coefficient de $f$.
Exemple : Soit $f$ une fonction affine tel que : $f(-2)=4$ et $f(5)=7$. Calculons $f(8)$.
On sait que :$$\frac{{f\left( 8 \right) -f\left( 5 \right)}}{{8 -5}} = \frac{{f\left( { -2} \right) -f\left( 5 \right)}}{{ -2 -5}}\,\,\,\left(\text{Coefficient de la fonction affine } f \right)$$Donc : \[\frac{{f\left( 8 \right) -7}}{3} = \frac{{4 -7}}{{ -7}}\]Donc : \[f\left( 8 \right) -7 = \frac{9}{7}\]Donc : \[f\left( 8 \right) = \frac{9}{7} + 7\]D’où : \[f\left( 8 \right) = \frac{{58}}{7}\]
Représentation graphique d’une fonction affine
- $M(x;y)$ est un point de $\left(C_f\right)$ signifie que : $f(x)=y.$
Exemple : Représentation graphique de la fonction affine $g$ définie par : $g(x)=3x-2.$
On calcule :
$$\begin{aligned}
g(0) &= 3 \times 0 -2 = -2\\
g(1) &= 3 \times 1 -2 = 1
\end{aligned}$$
Ainsi, la représentation graphique de $g$ est la droite $(\Delta)$ qui passe par les points $A(0;-2)$ et $B(1;1)$.
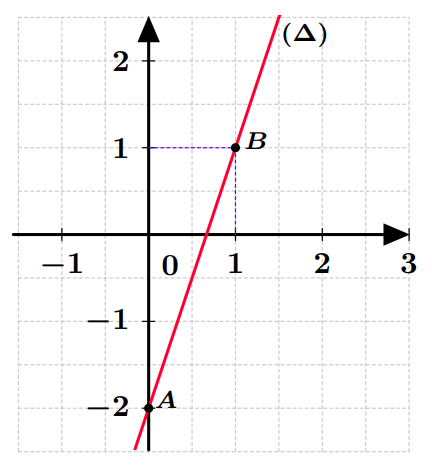
- La représentation graphique d’une fonction constante est parallèle à l’axe des abscisses.
- La représentation graphique d’une fonction nulle est l’axe des abscisses.
Fonction linéaire
La relation $f$ qui, à tout nombre réel $x$, associe le produit $ax$, est appelée fonction linéaire de coefficient $a$.
On la note : $$f : x \mapsto ax$$ Le nombre $ax$ est l’image de $x$ par $f$, et on écrit : $f(x)=ax$, $\quad \Big(f(x)$ se lit « $f$ de $x$ »$\Big)$.
Exemple :
Le périmètre d’un triangle équilatéral est proportionnel à la longueur de son côté.
Soit $x$ la longueur du côté, alors le périmètre de ce triangle est : $3x$.
Ainsi, on définit la fonction linéaire $p$ telle que : $p(x) = 3x$
L’image de $4$ par $p$ se note $p(4)$ :
$$p(4) = 3 \times 4 = 12$$
Donc, $12$ est l’image de $4$ par la fonction linéaire $p$.
De même, $4$ est l’antécédent de $12$ par la fonction linéaire $p$.
- Ne pas confondre $p(4)$ et $p\times (4)$.
- Pour calculer $f(x)$, on multiplie $x$ par $a$ le coefficient de la fonction linéaire.
Coefficient d’une fonction linéaire
Exemple : Soit $f$ une fonction linéaire tel que : $f(-5)=20$. Calculons $f(-7)$.
$f$ est une fonction linéaire, donc $f(x)=ax$.
Or : $f(-5)=20$, alors : $$a=\dfrac{f(-5)}{-5}=\dfrac{20}{-5}=-4.$$
Par conséquent : $$f(x)=-4x.$$
Donc : $$f(-7)=-4\times (-7)=28.$$
Représentation graphique d’une fonction linéaire
- La représentation graphique ou la courbe d’une fonction linéaire $f$ est notée $(C_f)$ ou $(D)$.
- $M(x;y)$ est un point de $\left(C_f\right)$ signifie que : $f(x)=y.$
Exemple : Représentation graphique de la fonction linéaire $f$ définie par : $f(x)=2x.$
On calcule :
$$f(1) = 2 \times 1 = 2$$
Ainsi, la représentation graphique de $f$ est la droite $(D)$ qui passe par l’origine $O(0;0)$ du repère et par le point $A(1;2)$.
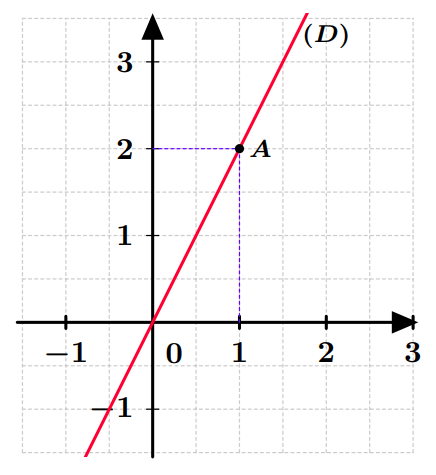
On a toujours : $$f(0) = 0 \quad \text{et} \quad f(1) = a$$
Système de deux équations à deux inconnues du premier degré
$$\left\{ \begin{array}{l}
ax + by = c\\
dx + ey = f
\end{array} \right.$$où $a$, $b$, $c$, $d$, $e$ et $f$ sont des nombres réels donnés.
- $x$ et $y$ sont les inconnues.
- Un couple $(x ; y)$ vérifiant les deux équations en même temps, est une solution du système.
Exemples :
$$\left\{ \begin{aligned}
& 2x -3y = 7\\
& x + 5y = -3
\end{aligned} \right. ~~;~~
\left\{ \begin{aligned}
& \sqrt 2 x + \dfrac{2}{3}y = 5\\
& -x + \sqrt 3 y = \dfrac{{ -1}}{2}
\end{aligned} \right.~~;~~
\left\{ \begin{aligned}
&\dfrac{{x + 2}}{3} + \dfrac{{y -4}}{2} = -6\\
&\dfrac{{4x + 1}}{5} + \dfrac{{3y}}{2} = -4
\end{aligned} \right.$$Ce sont des systèmes de deux équations à deux inconnues du premier degré.
Exemple : Le couple $(5;9)$ est une solution du système : $$\left\{ \begin{aligned}
& 2x -y = 1\\
& -4x + 3y = 7
\end{aligned} \right.$$ Car :
$$\left\{ \begin{aligned}
& 2 \times 5 -9 = 10 -9 = 1\\
& -4 \times 5 + 3 \times 9 = -20 + 27 = 7
\end{aligned} \right.$$
Résolution algébrique d’un système
Méthode de substitution
Exemple : Résoudre, par substitution, le système suivant :
$$
\begin{cases}
2x -3y = 7 & (1) \\
x + 5y = -3 & (2)
\end{cases}
$$
Dans l’équation $(2)$, on exprime $x$ en fonction de $y$ :
$$
\boxed{x = -3 -5y} \quad (3)
$$
On remplace $x$ par $-3 -5y$ dans l’équation $(1)$ :
$$
\begin{array}{c}
2(-3 -5y) -3y = 7 \\
-6 -10y -3y = 7 \\
-6 -13y = 7 \\
-13y = 13 \\
y = \frac{13}{-13} \\
y = -1
\end{array}
$$
On remplace $y = -1$ dans l’équation $(3)$ :
$$
\begin{aligned}
x &= -3 -5\times (-1) \\
x &= -3 + 5 \\
x &= 2
\end{aligned}
$$
Donc la solution du système est le couple :
$$
\boxed{(2 \, ; \, -1)}
$$
Méthode de combinaison linéaire
Exemple : Résoudre, par combinaison linéaire, le système :
$$
\begin{cases}
3x -4y = 32 & (1) \\
7x -6y = 58 & (2)
\end{cases}
$$
Pour éliminer $y$, on multiplie l’équation $(1)$ par $-3$ et l’équation $(2)$ par $2$. On obtient :
$$
\begin{cases}
-9x + 12y = -96 & (3) \\
14x -12y = 116 & (4)
\end{cases}
$$
On additionne les équations $(3)$ et $(4)$ membre à membre :
$$
-9x + 12y + 14x -12y = -96 + 116 \\
5x = 20 \\
x = \frac{20}{5} \\
\boxed{x = 4}
$$
Pour éliminer $x$, on multiplie l’équation $(1)$ par $7$ et l’équation $(2)$ par $-3$. On obtient :
$$
\begin{cases}
21x -28y = 224 & (5) \\
-21x + 18y = -174 & (6)
\end{cases}
$$
On additionne les équations $(5)$ et $(6)$ membre à membre :
$$
21x -28y -21x + 18y = 224 -174 \\
-10y = 50 \\
y = \frac{50}{-10} \\
\boxed{y = -5}
$$
Donc la solution du système est le couple :
$$
\boxed{(4 \, ; \, -5)}
$$
Résolution graphique d’un système
Exemple 1 : Résoudre graphiquement le système :
$$
\begin{cases}
2x + y = 3 \\
x + y = 1
\end{cases}
$$
On considère les droites associées :
$$
\begin{cases}
(D):~ y = -2x + 3 \\
(L):~ y = -x + 1
\end{cases}
$$
Les droites $(D)$ et $(L)$ n’ont pas le même coefficient directeur. Donc, elles sont sécantes.
Soit $A$ le point d’intersection de $(D)$ et $(L)$.
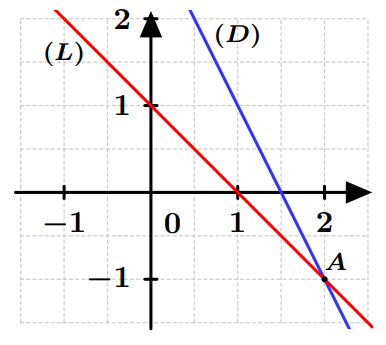
Exemple 2 : Résoudre graphiquement le système :
$$
\begin{cases}
x -2y = 5 \\
-2x + 4y = 8
\end{cases}
$$
On considère les droites associées :
$$
\begin{cases}
(D):~ y = \dfrac{1}{2}x -\tfrac{5}{2} \\
(L):~ y = \dfrac{1}{2}x + 2
\end{cases}
$$
Les droites $(D)$ et $(L)$ ont le même coefficient directeur mais des ordonnées à l’origine différentes. Donc, elles sont strictement parallèles.
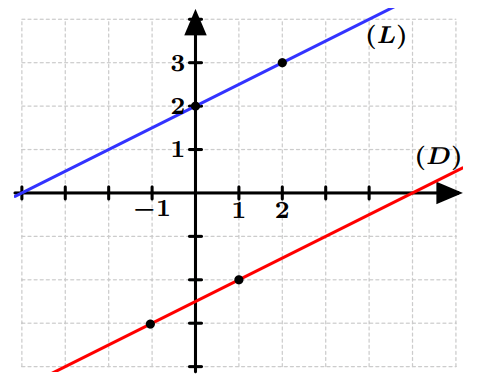
Résolution de problèmes
Si la valeur totale de ces billets est de $500$ dirhams, déterminer le nombre de billets de chaque espèce.
- Choix des inconnues :Soit $x$ le nombre de billets de $20$ DH.
Soit $y$ le nombre de billets de $50$ DH.
- Mise en système :Le nombre total de billets est $13$, donc :
$$x + y = 13 \quad (1)$$La valeur totale des billets est $500$ DH, donc :
$$20x + 50y = 500 \quad (2)$$Donc le système est : $$\begin{cases}
x + y = 13 & {(1)} \\
20x + 50y = 500& {(2)}
\end{cases} $$ - Résolution :D’après $(1)$ :
$$y = 13 -x \quad (3)$$On remplace $y$ dans $(2)$ :
\[
\begin{array}{c}
20x + 50(13 -x) = 500 \\
20x + 650 -50x = 500 \\
-30x + 650 = 500 \\
-30x = -150 \\
x = \frac{-150}{-30} \\
\boxed{x = 5}
\end{array}
\]On remplace $x = 5$ dans $(3)$ :
$$y = 13 -5 = \boxed{8}$$ - Vérification :
$$
\begin{cases}
5 + 8 = 13 \\
20 \times 5 + 50 \times 8 = 100 + 400 = 500
\end{cases}
$$ - Conclusion :
Yassine possède 5 billets de 20 DH et 8 billets de 50 DH.





